仮説検定とは | データサイエンティスト統計学の基礎 | AI起業ラボ｜初心者でも月5万円稼げる副業から本格ビジネスまで

仮説検定の基礎
- 仮説検定の目的
- 帰無仮説と対立仮説
仮説検定の手順
具体的な仮説検定の例：母分散が既知の場合の母平均についての仮説検定
仮説検定の注意点

データサイエンティストの必須知識、「仮説検定とは | 統計学の基礎」について解説します。

仮説検定の基礎

仮説検定は、統計学の中でとても重要な手法の一つです。具体的なデータをもとに、ある仮説が正しいかどうかを判断するための方法です。以下で、仮説検定の目的や、その中心的な考え方である「帰無仮説」と「対立仮説」について詳しく見ていきましょう。

仮説検定の目的

仮説検定の主な目的は、観測されたデータがある特定の仮説の下で期待されるデータと一致するかどうかを判断することです。例えば、新しい薬が既存の薬よりも効果的であるかを調べる際に、仮説検定を使用できます。

具体的には、以下のような疑問に答えるために使用されます。

ある治療法Aと治療法B、どちらが効果的か？
広告キャンペーンの前後で、商品の売上が実際に増加したか？
男性と女性の間で、ある特定の能力テストのスコアに差はあるか？

これらの疑問に答えるために、仮説検定はとても強力なツールとなります。

帰無仮説と対立仮説

仮説検定を行う際の基本的な考え方は、2つの仮説を設定し、データをもとにそのどちらが正しいかを評価することです。これらの2つの仮説は「帰無仮説」と「対立仮説」と呼ばれます。

帰無仮説 (Null Hypothesis, \(H_0\)): 通常、変化がない、差がないという状態を表す仮説です。例えば、2つの治療法の効果に差がない、新しい広告の効果がないなど。
対立仮説 (Alternative Hypothesis, \(H_1\) or \(H_a\)): 帰無仮説に対して、何らかの変化がある、差があるという状態を表す仮説です。例えば、治療法Aの方が治療法Bより効果的である、新しい広告の後で売上が増加したなど。

以下に具体的な例を紹介します。

考え方としては、ある学校で新しい教育方法を導入した後の学生のテストスコアを評価したいとします。この場合、以下のように帰無仮説と対立仮説を設定できます。

\(H_0\): 新しい教育方法を導入した後も、学生のテストスコアに変化はない。
\(H_a\): 新しい教育方法を導入した後、学生のテストスコアは変化する。

この2つの仮説を基に、実際のデータを分析して、帰無仮説を受け入れるか、あるいは棄却するかを判断します。

仮説検定の手順

仮説検定は、特定の手順に沿って行われます。この手順を理解することで、仮説検定の目的や意味がより明確になります。以下にその手順を説明します。

1. 帰無仮説と対立仮説の設定

まず、検討する仮説を設定します。これには、帰無仮説（\(H_0\)）と対立仮説（\(H_a\)）の2つがあります。

帰無仮説（\(H_0\)）: 通常、変化がない、差がないという状態を表します。
対立仮説（\(H_a\)）: 帰無仮説に反する状態、つまり変化がある、差があるという状態を表します。

例えば、ある製品の生産ラインの不良品率が5%とされている場合、

\(H_0: p = 0.05\) （不良品率は5%である）
\(H_a: p \neq 0.05\) （不良品率は5%ではない）

と設定できます。

2. 有意水準の選択

有意水準は、帰無仮説を誤って棄却するリスクをどれだけ許容するかを示す値です。通常、1%、5%、10%などの値が使用されます。例えば、有意水準を5%と設定した場合、5%の確率で帰無仮説を誤って棄却するリスクを受け入れることを意味します。

有意水準の選択を説明するためのグラフとして、正規分布のグラフを描き、有意水準に応じた棄却域を色分けして示しましょう。

片側検定のグラフ（右側のみの検定）

import matplotlib.pyplot as plt
import numpy as np

# Define the distribution parameters
mean = 0
std_dev = 1

# Create an array of x values
x = np.linspace(-4, 4, 1000)

# Calculate the PDF of the normal distribution
pdf = stats.norm.pdf(x, mean, std_dev)

# Define the critical value for alpha = 0.05
critical_value = stats.norm.ppf(1 - 0.05)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, 'b-', label='Normal Distribution')
plt.fill_between(x, pdf, where=(x > critical_value), color='red', label='Rejection Region (α = 0.05)')
plt.axvline(critical_value, color='black', linestyle='--', label=f'Critical Value: {critical_value:.2f}')
plt.title('Selection of Significance Level (α = 0.05)')
plt.xlabel('Z Value')
plt.ylabel('Probability Density Function')
plt.legend()
plt.grid(True)
plt.show()

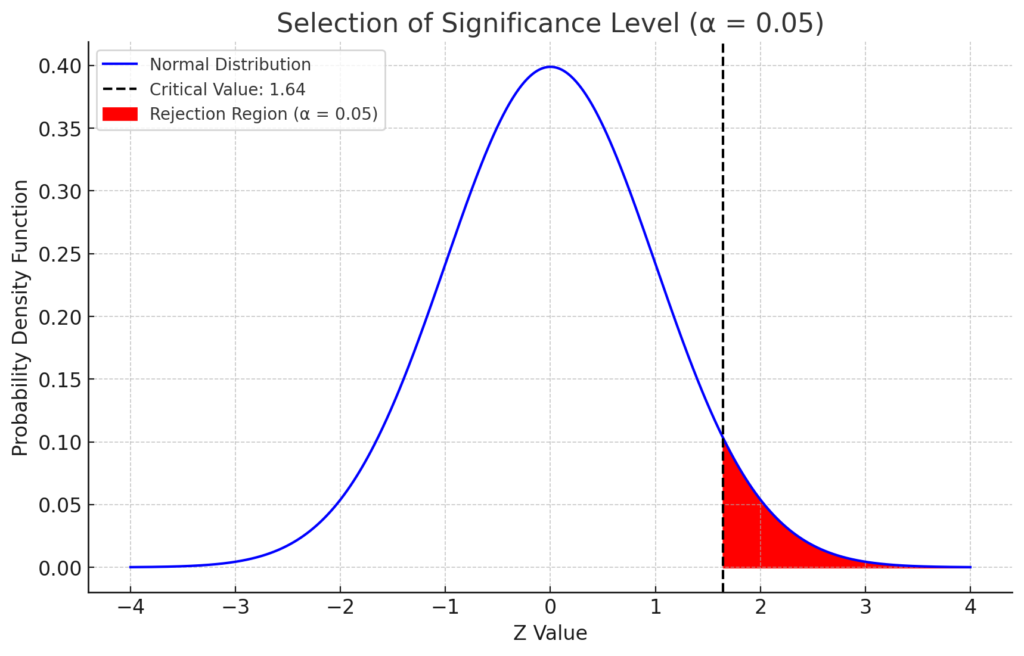
こちらが有意水準（α）を5%とした場合の正規分布のグラフです。赤色の部分が棄却域を示しており、この範囲内の値が得られた場合に帰無仮説を棄却します。破線は棄却域の境界（臨界値）を示しています。

このグラフから、有意水準を5%と設定すると、正規分布の右端の5%の範囲が棄却域となることが視覚的に理解できます。

両側検定のグラフ

「両側検定」は、帰無仮説が棄却される範囲が正規分布の両端に存在する場合の検定です。有意水準 \( \alpha \) の半分が右側の尾部に、残りの半分が左側の尾部に割り当てられます。

# Define the critical values for two-tailed test with alpha = 0.05
critical_value_left = stats.norm.ppf(0.05 / 2)
critical_value_right = stats.norm.ppf(1 - (0.05 / 2))

# Plotting for two-tailed test
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, 'b-', label='Normal Distribution')
plt.fill_between(x, pdf, where=((x < critical_value_left) | (x > critical_value_right)), 
                 color='red', label='Rejection Region (α = 0.05/2 each tail)')
plt.axvline(critical_value_left, color='black', linestyle='--', 
            label=f'Critical Value Left: {critical_value_left:.2f}')
plt.axvline(critical_value_right, color='black', linestyle='--', 
            label=f'Critical Value Right: {critical_value_right:.2f}')
plt.title('Two-Tailed Test (α = 0.05)')
plt.xlabel('Z Value')
plt.ylabel('Probability Density Function')
plt.legend()
plt.grid(True)
plt.show()

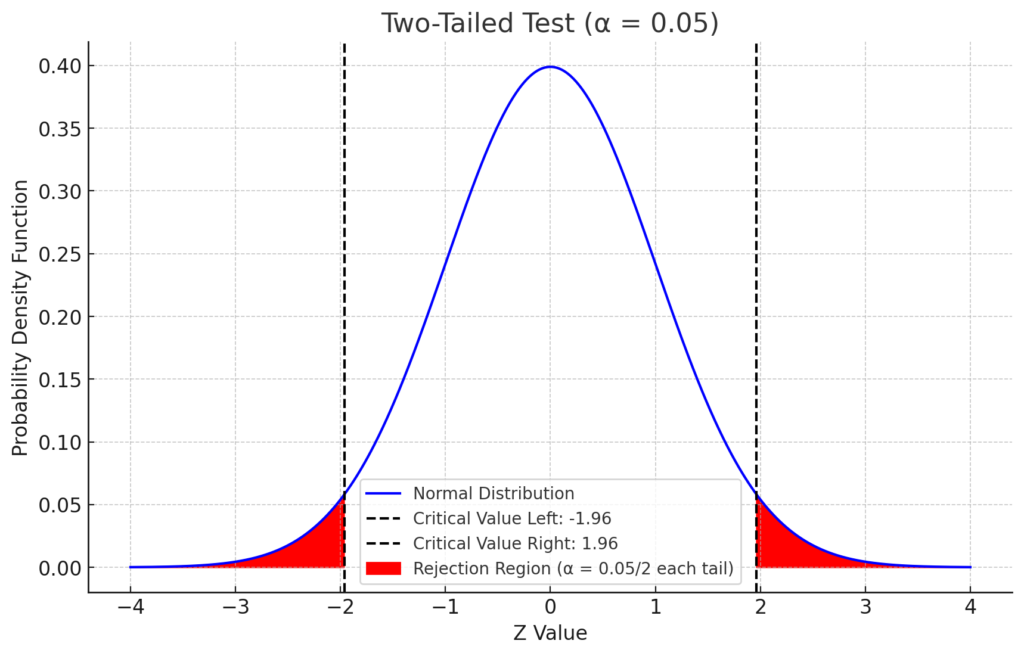
こちらが有意水準（\( \alpha \)）を5%とした場合の「両側検定」の正規分布のグラフです。赤色の部分が棄却域を示しており、この範囲内の値が得られた場合に帰無仮説を棄却します。2本の破線はそれぞれ棄却域の境界（左側および右側の臨界値）を示しています。

このグラフから、有意水準を5%と設定すると、正規分布の両端の2.5%ずつ（合計5%）の範囲が棄却域となることが視覚的に理解できます。

3. 検定統計量の計算

次に、実際のデータを用いて検定統計量を計算します。この検定統計量は、帰無仮説が正しいと仮定した場合の期待される分布と、実際のデータの間の差を示すものです。

例えば、平均値に関する仮説検定の場合、Z検定を使用できます。Z検定の検定統計量は以下の式で計算されます。

\[
Z = \frac{\bar{X} – \mu_0}{\sigma / \sqrt{n}}
\]

ここで、

\( \bar{X} \) は標本平均
\( \mu_0 \) は帰無仮説のもとでの母平均
\( \sigma \) は母標準偏差
\( n \) は標本数

です。

import numpy as np

# Sample data
data = np.array([24.5, 25.6, 26.7, 24.2, 25.3])

# Known parameters
mu_0 = 25
sigma = 2
n = len(data)

# Calculate Z statistic
z_stat = (np.mean(data) - mu_0) / (sigma / np.sqrt(n))
z_stat

0.29068883707497045

この検定統計量を用いて、次のステップで帰無仮説を受け入れるか棄却するかを判断します。

4. 棄却域の決定

検定統計量がどの範囲に入ると帰無仮説を棄却するかを決める領域を「棄却域」と言います。有意水準と検定の種類（片側検定 or 両側検定）に基づき、この棄却域を決定します。

例えば、有意水準を5%とした片側検定の場合、Z検定ではZ値が1.645以上なら帰無仮説を棄却します。

import scipy.stats as stats

alpha = 0.05
critical_value_right = stats.norm.ppf(1 - alpha)
critical_value_right

1.6448536269514722

5. 検定統計量と棄却域の比較

計算した検定統計量が棄却域に入るかどうかを確認します。棄却域に入る場合、帰無仮説を棄却します。

z_statistic = 1.8  # 仮に計算したZ値として

if z_statistic > critical_value_right:
    result = "Reject the null hypothesis"
else:
    result = "Do not reject the null hypothesis"
result

Reject the null hypothesis

6. 結果の解釈

仮説検定の結果を解釈する際には、以下の2つの結論のいずれかになります。

帰無仮説を棄却する: 検定統計量が棄却域に入った場合、帰無仮説は棄却され、対立仮説が採用されます。
帰無仮説を受容する: 検定統計量が棄却域に入らない場合、帰無仮説は受容されます。ただし、これは帰無仮説が「正しい」ということを意味するわけではありません。データに基づいて、帰無仮説を棄却する十分な証拠が得られなかったと解釈されます。

例の場合、Z値が1.8で、棄却域の境界が1.645であるため、帰無仮説を棄却します。この結果は、新しい教育方法が学生のテストスコアに影響を与える可能性をを示唆しています。

具体的な仮説検定の例：母分散が既知の場合の母平均についての仮説検定

仮説検定の理解を深めるために、具体的な例を通してその手順を確認してみましょう。

問題設定

ある学校で新しい教育方法を導入した後、生徒たちのテストスコアが向上したかどうかを確かめるための仮説検定を実施したいとします。

既知の情報：新しい教育方法を導入する前のテストスコアの平均は50点、母分散は100である。
新しい教育方法を導入した後のサンプル：5人の生徒のテストスコアは [53, 54, 57, 52, 56] である。

帰無仮説と対立仮説の設定

このデータを基に、新しい教育方法がテストスコアに効果があったかどうかを確かめるための仮説を設定します。

帰無仮説（\(H_0\)）: 新しい教育方法はテストスコアに効果がない（つまり、母平均は50点である）。
対立仮説（\(H_a\)）: 新しい教育方法はテストスコアを向上させた（つまり、母平均は50点より大きい）。

数式で表すと以下のようになります。
\[
H_0: \mu = 50
\]
\[
H_a: \mu > 50
\]

ここで、\(\mu\) は母平均を示します。

この帰無仮説と対立仮説をもとに、実際のサンプルデータと比較して、新しい教育方法の効果について統計的に評価します。

検定統計量の計算方法

検定統計量は、サンプルデータが帰無仮説に従っている場合の期待値との差を、標準偏差で割った値として計算されます。この検定統計量が大きければ大きいほど、帰無仮説との乖離が大きいことを示します。

Z値の計算

Z値は、以下の式で計算される検定統計量です。

\[
Z = \frac{\bar{X} – \mu}{\sigma / \sqrt{n}}
\]

ここで、

\( \bar{X} \) はサンプルの平均値
\( \mu \) は帰無仮説のもとでの母平均
\( \sigma \) は母集団の標準偏差
\( n \) はサンプルサイズ

を示します。

例題:
以前取り上げた、新しい教育方法の効果に関するデータをもとに、Z値を計算してみましょう。

既知の情報として、母平均は50点、母分散は100であり、サンプルとして5人の生徒のテストスコアは [53, 54, 57, 52, 56] でした。

以下のPythonコードでZ値を計算できます。

import numpy as np

# Given data
scores = np.array([53, 54, 57, 52, 56])
mu = 50
sigma = 10  # square root of variance
n = len(scores)

# Calculate sample mean
sample_mean = np.mean(scores)

# Calculate Z value
z_value = (sample_mean - mu) / (sigma / np.sqrt(n))
z_value

0.9838699100999071

このZ値が大きい場合、新しい教育方法が生徒のテストスコアに効果をもたらした可能性が高いことを示唆しています。具体的な棄却の判断は、次の「棄却域の決定」で行います。

棄却域の決定

仮説検定において、帰無仮説を棄却するかどうかの判断基準となる領域を「棄却域」と呼びます。この領域は、有意水準と関連して設定されます。

例として、有意水準を5%（0.05）とした場合の右側検定を考えます。この場合、Z値の分布において、右端の5%の領域が棄却域となります。

Pythonを使用して、Z値の分布から5%の有意水準での棄却域を見つけることができます。

import scipy.stats as stats

# Define significance level
alpha = 0.05

# Find critical Z value for right-tailed test
z_critical = stats.norm.ppf(1 - alpha)
z_critical

1.6448536269514722

このコードは、右側検定のための有意水準5%における臨界Z値を計算します。

結果の解釈

帰無仮説の棄却と受容

Z値の計算結果と臨界Z値を比較することで、帰無仮説の棄却または受容を決定します。

計算されたZ値 > 臨界Z値の場合: 帰無仮説を棄却
計算されたZ値 ≤ 臨界Z値の場合: 帰無仮説を受容

例として、先ほどの教育方法の例で計算されたZ値が2.2だったと仮定します。この場合、臨界Z値が約1.645であれば、2.2 > 1.645となるため、帰無仮説を棄却します。これは、新しい教育方法がテストスコアに統計的に有意な効果をもたらした可能性が高いことを示しています。

仮説検定の注意点

第一種の誤りと第二種の誤り

仮説検定では、誤った結論を導くリスクが常に存在します。これらの誤りは、第一種の誤りと第二種の誤りとして知られています。

第一種の誤り（Type I error）: 帰無仮説が真実であるにもかかわらず、それを誤って棄却する誤り。この確率は有意水準（α）として設定されます。例えば、α=0.05の場合、100回の検定のうち約5回は第一種の誤りを犯す可能性がある。
第二種の誤り（Type II error）: 対立仮説が真実であるにもかかわらず、帰無仮説を誤って受容する誤り。この確率はβとして示されます。第二種の誤りの確率は、検出力（1-β）と密接に関連しています。

\[
\text{検出力} = 1 – \beta
\]

検出力は、対立仮説が真実である場合にそれを正しく検出する能力を意味します。