データサイエンティストの必須知識、「仮説検定の方法 | 統計学の基礎」について解説します。
仮説検定の具体的な手順とは
仮説検定の基本
仮説検定とは
仮説検定は、統計学において特定の仮説がデータに基づいて妥当かどうかを判断する方法です。具体的には、観測されたデータがある仮説の下でどれだけあり得るか、あるいはその逆かを評価します。
例:新製品Aと既存製品Bの効果を比較したい場合、2つの製品の効果に差がないという仮説(帰無仮説)を立て、データを収集してその仮説が妥当かどうかを評価します。
帰無仮説と対立仮説
- 帰無仮説(\( H_0 \)):仮説検定の初期段階で立てられる仮説。たとえば、2つのグループ間に差がないという仮説。
- 対立仮説(\( H_1 \) or \( H_a \)):帰無仮説に対する反対の仮説。例えば、2つのグループ間に差があるという仮説。
有意水準とp値
有意水準(\( \alpha \)):帰無仮説を誤って棄却するリスクを示す閾値。通常、0.05や0.01などの値が使用される。
p値:サンプルデータから計算される値で、帰無仮説が真実であると仮定した場合に、現在のデータまたはそれよりも極端なデータが得られる確率を示す。
例:p値が0.03で、有意水準が0.05の場合、p値は有意水準より小さいため、帰無仮説を棄却します。
第一種の誤りと第二種の誤り
- 第一種の誤り(Type I error):帰無仮説が真実である場合に、それを誤って棄却するリスク。この確率は有意水準(\( \alpha \))として設定される。
- 第二種の誤り(Type II error):対立仮説が真実である場合に、帰無仮説を誤って受け入れるリスク。この確率は\( \beta \)として示され、検出力(1-\( \beta \))と関連している。
\[
\text{検出力} = 1 – \beta
\]
検出力は、対立仮説が真実である場合にそれを正しく検出する能力を示します。
片側検定
片側検定の定義
片側検定は、ある値よりも大きい(または小さい)という一方向の差を検出するための仮説検定方法です。帰無仮説の下での平均値とサンプルの平均値との間に、特定の方向にだけ差があるかを評価します。
右側検定と左側検定
- 右側検定: サンプルの平均値が帰無仮説の下での平均値よりも大きいかどうかを検討する場合の検定。
- 左側検定: サンプルの平均値が帰無仮説の下での平均値よりも小さいかどうかを検討する場合の検定。
右側検定と左側検定のグラフ
まず、右側検定と左側検定の棄却域を示す正規分布のグラフを描きます。これにより、どの部分が棄却域であるかを明示できます。
以下のPythonコードで、右側検定と左側検定のグラフを描画します。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# Define the distribution parameters
mean = 0
std_dev = 1
# Create an array of x values
x = np.linspace(-4, 4, 1000)
# Calculate the PDF of the normal distribution
pdf = stats.norm.pdf(x, mean, std_dev)
# Define the critical values for alpha = 0.05
critical_value_right = stats.norm.ppf(1 - 0.05)
critical_value_left = stats.norm.ppf(0.05)
# Plotting
fig, ax = plt.subplots(1, 2, figsize=(15, 6))
# Right-tailed test
ax[0].plot(x, pdf, 'b-', label='Normal Distribution')
ax[0].fill_between(x, pdf, where=(x > critical_value_right), color='red', label='Rejection Region (α = 0.05)')
ax[0].axvline(critical_value_right, color='black', linestyle='--', label=f'Critical Value: {critical_value_right:.2f}')
ax[0].set_title('Right-Tailed Test')
ax[0].legend()
ax[0].grid(True)
# Left-tailed test
ax[1].plot(x, pdf, 'b-', label='Normal Distribution')
ax[1].fill_between(x, pdf, where=(x < critical_value_left), color='red', label='Rejection Region (α = 0.05)')
ax[1].axvline(critical_value_left, color='black', linestyle='--', label=f'Critical Value: {critical_value_left:.2f}')
ax[1].set_title('Left-Tailed Test')
ax[1].legend()
ax[1].grid(True)
plt.tight_layout()
plt.show()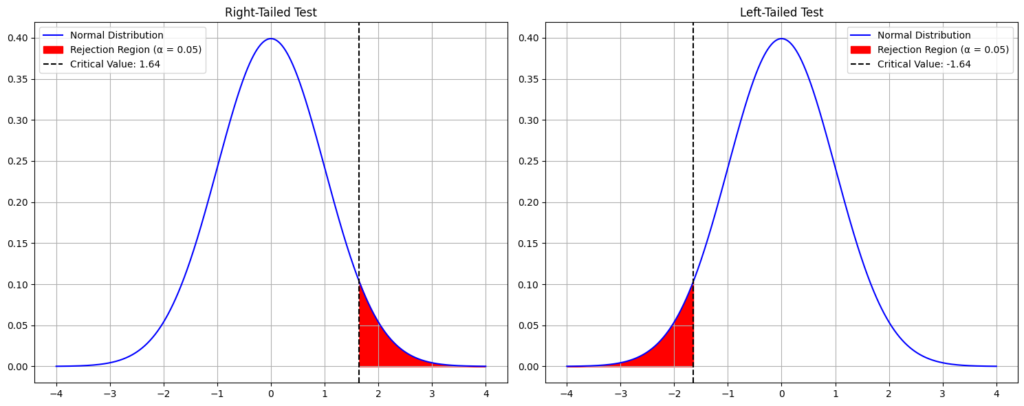
以上のグラフは、右側検定と左側検定の棄却域を示しています。
- 右側検定: 赤色の部分が棄却域となり、この範囲内の値が得られた場合に帰無仮説を棄却します。破線は棄却域の境界(臨界値)を示しています。
- 左側検定: 同様に、赤色の部分が棄却域となります。
これらのグラフを参考に、片側検定の仕組みや、棄却域がどの部分に位置するのかを理解できます。
片側検定の実施手順
- 帰無仮説と対立仮説の設定:
例: \( H_0: \mu \geq \mu_0 \) と \( H_a: \mu < \mu_0 \)(左側検定の場合) - 適切な検定統計量の選択と計算:
例: Z値やt値 - p値の計算:
- p値と有意水準の比較:
例: \( p < \alpha \) であれば帰無仮説を棄却。 - 結果の解釈:
帰無仮説を棄却するか、受け入れるかに基づいて結論を導き出します。
p値の計算: Pythonコード例:
from scipy.stats import t
t_statistic = # 計算されたt値
df = # 自由度
p_value = t.cdf(t_statistic, df)両側検定
両側検定の定義
両側検定は、ある値からのどちらかの方向の差、つまり大きいか小さいかを問わず差があるかを検出するための仮説検定方法です。この検定では、帰無仮説の下での平均値とサンプルの平均値との間に差があるかを評価します。
両側検定の実施手順
- 帰無仮説と対立仮説の設定:
例: \( H_0: \mu = \mu_0 \) と \( H_a: \mu \neq \mu_0 \) - 適切な検定統計量の選択と計算:
例: Z値やt値 - p値の計算:
両側検定では、片側p値を2倍して得られるp値を使用します。 - p値と有意水準の比較:
例: \( p < \alpha \) であれば帰無仮説を棄却。 - 結果の解釈:
帰無仮説を棄却するか、受け入れるかに基づいて結論を導き出します。
p値の計算: Pythonコード例:
from scipy.stats import t
t_statistic = # 計算されたt値
df = # 自由度
one_sided_p_value = t.cdf(t_statistic, df)
p_value = 2 * one_sided_p_value if t_statistic < 0 else 2 * (1 - one_sided_p_value)片側検定と両側検定の違い
片側検定は、ある方向の差(例: 大きいか小さいか)のみを検出するのに対し、両側検定はどちらの方向の差も検出します。
具体的な違いを視覚的に示すため、両側検定の棄却域を示すグラフを描画します。
# Calculate the critical values for alpha = 0.05 for a two-tailed test
critical_value_right_2tail = stats.norm.ppf(1 - 0.025)
critical_value_left_2tail = stats.norm.ppf(0.025)
# Plotting
plt.figure(figsize=(8, 6))
# Two-tailed test
plt.plot(x, pdf, 'b-', label='Normal Distribution')
plt.fill_between(x, pdf, where=(x > critical_value_right_2tail) | (x < critical_value_left_2tail),
color='red', label='Rejection Region (α = 0.05)')
plt.axvline(critical_value_right_2tail, color='black', linestyle='--',
label=f'Right Critical Value: {critical_value_right_2tail:.2f}')
plt.axvline(critical_value_left_2tail, color='black', linestyle='--',
label=f'Left Critical Value: {critical_value_left_2tail:.2f}')
plt.title('Two-Tailed Test')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
上記のグラフは、両側検定の棄却域を示しています。
赤色の部分は、両側検定の棄却域となります。この範囲内の値が得られた場合、帰無仮説を棄却します。破線は棄却域の境界(臨界値)を示しています。
このグラフを参考にして、両側検定がどのように動作するか、そして片側検定とどのように異なるかを理解できます。
母分散が未知の場合の仮説検定
母分散未知時の検定の必要性
実際のデータ解析では、母集団の分散が未知の場合が多いです。Z検定は、母分散が既知の場合にのみ適用されます。しかし、母分散が未知の場合、サンプル分散を用いてZ検定を行うと、実際の検定統計量の分布が正規分布から逸脱する可能性があります。この問題を解決するために、t検定が導入されました。
t検定の導入
t検定は、母分散が未知の場合に仮説検定を行うための方法です。サンプルサイズが小さい場合や母分散が未知の場合に特に有効です。t検定では、t分布を使用して、サンプル分散を用いた検定統計量の分布を近似します。
t検定の実施手順
- 帰無仮説と対立仮説の設定
- サンプルから必要な統計量を計算: サンプルの平均、サンプルの標準偏差、サンプルサイズ
- t値の計算:
\[ t = \frac{\text{サンプル平均} – \text{母平均}}{\text{サンプル標準偏差} / \sqrt{\text{サンプルサイズ}}} \] - p値の計算: t分布を用いて
- p値と有意水準の比較: \( p < \alpha \) であれば帰無仮説を棄却
Z検定とt検定の違い
- Z検定:
母分散が既知の場合に使用
正規分布を基にした検定
大きなサンプルサイズに適している - t検定:
母分散が未知の場合やサンプルサイズが小さい場合に使用
t分布を基にした検定
サンプルサイズが小さくても適切な検定が可能
視覚的な理解のため、正規分布とt分布の違いをグラフで示します。
# Define the distribution parameters
df = 10 # degrees of freedom for the t-distribution
# Calculate the PDF of the normal distribution and t-distribution
pdf_norm = stats.norm.pdf(x, mean, std_dev)
pdf_t = stats.t.pdf(x, df)
# Plotting
plt.figure(figsize=(8, 6))
plt.plot(x, pdf_norm, 'b-', label='Normal Distribution')
plt.plot(x, pdf_t, 'r-', label=f't-Distribution (df={df})')
plt.title('Comparison of Normal Distribution and t-Distribution')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()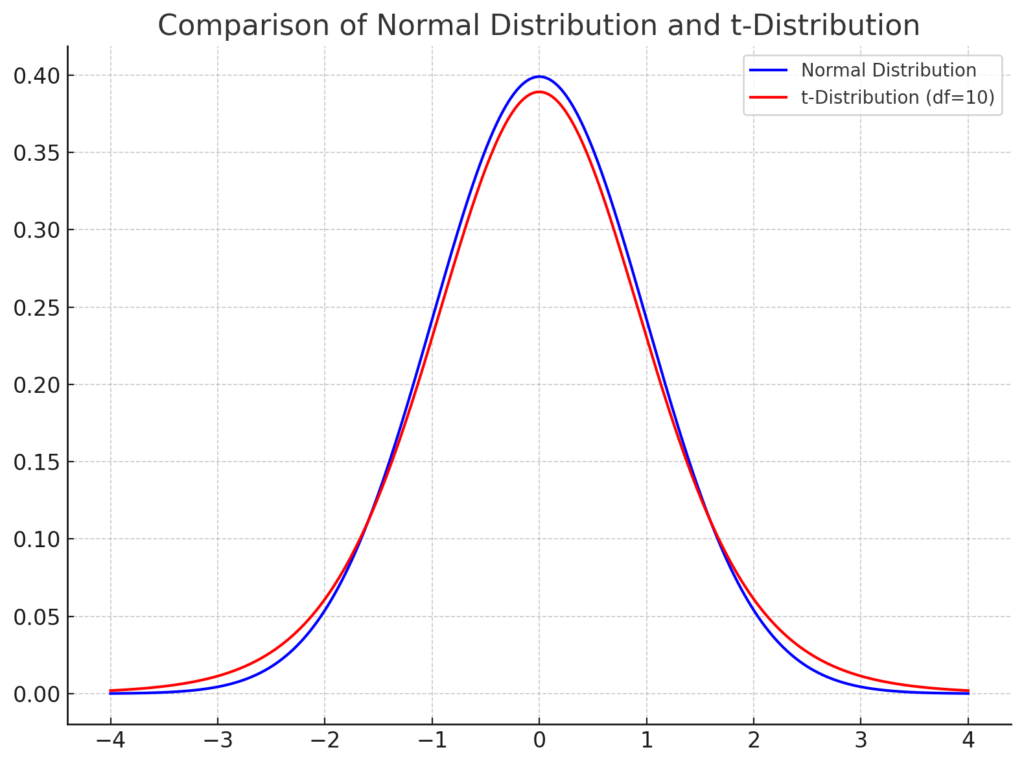
上記のグラフは、正規分布(青)とt分布(赤)を比較しています。
t分布は、自由度(サンプルサイズ – 1)に依存します。自由度が小さいとき、t分布は正規分布よりも太く、尾が重くなります。これは、小さいサンプルサイズでは、サンプルの平均値の変動が大きいためです。
しかし、自由度が大きくなると、t分布は正規分布に近づきます。これは、サンプルサイズが大きくなると、中心極限定理により、サンプル平均の分布が正規分布に従うようになるためです。
このグラフを参考にして、Z検定とt検定の違いと、t分布の特性を理解できます。

▼AIを使った副業・起業アイデアを紹介♪
