データサイエンティストの必須知識、「データを客観的に分析する | 統計学の基礎」について解説します。
情報の客観的な分析に用いられる主な手法
平均値
定義と目的
平均値(もしくは平均)は、データセットの中心傾向を表す基本的な統計量です。数学的には、データセット内の全ての数値を合計し、その数値の個数で割ったものになります。平均値は、データポイントが全体としてどこに集まっているかを示し、データセットの「平均的な」値を提供します。
数式で表すと:
\[ \text{平均値(Mean)} = \frac{\text{データの合計}}{\text{データの個数}} \]
計算方法
平均値の計算方法はシンプルです。データセット内の全ての数値を合計して、データの個数で割ります。
たとえば、テストのスコアが [80, 90, 85, 92, 88] だった場合、平均値は以下の通り計算できます。
\[ \text{Mean} = \frac{80 + 90 + 85 + 92 + 88}{5} \]
実例と解釈
以下にPythonコードを使用して、サンプルデータの平均値を計算します。このコードでは、NumPyという科学計算ライブラリを使用しています。
import numpy as np
# Sample Data: Test scores of 5 students
scores = [80, 90, 85, 92, 88]
# Calculating the mean
mean_score = np.mean(scores)
print(f"The mean test score is: {mean_score}")The mean test score is: 87.0このコードの実行結果、平均テストスコアが出力されます。解釈としては、この平均値が各テストスコアの「中心」を示しています。もちろん、実際のテストスコアがこの平均値からどれだけ離れているか(分散や標準偏差)も重要な情報となりますが、平均値はデータセット全体を一つの値で表現する際の出発点となります。
グラフで平均値を視覚化することもできます。以下のPythonコードは、テストスコアとその平均値を棒グラフで示しています。
import matplotlib.pyplot as plt
import numpy as np
# Data
students = ['A', 'B', 'C', 'D', 'E']
scores = [80, 90, 85, 92, 88]
# Mean calculation
mean_score = np.mean(scores)
# Creating bar plot
plt.bar(students, scores, color='blue')
plt.axhline(y=mean_score, color='r', linestyle='-')
# Adding labels and title
plt.xlabel("Students")
plt.ylabel("Scores")
plt.title("Test Scores of 5 Students with Mean Score Line")
plt.text(4.5,mean_score + 1, f'Mean: {mean_score}', color = 'red')
# Display the plot
plt.show()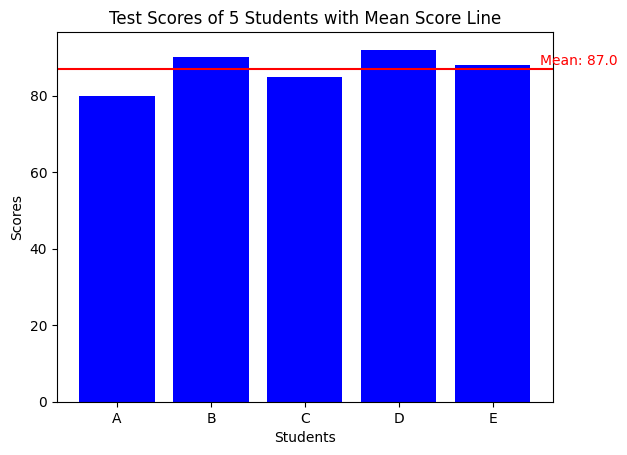
このグラフでは、赤い線が平均値を示しており、個々のスコアが平均値と比較してどのように分布しているかが視覚的に理解しやすくなっています。
分散と標準偏差
定義と目的
分散と標準偏差は、データセットのばらつきや散らばりを表す統計量です。平均値がデータの中心的な位置を示すのに対し、分散と標準偏差はデータが平均値の周りにどれだけ広がっているかを示します。
- 分散 (Variance): データポイントが平均からどれだけ離れているかの平均を示す。大きい分散は、データポイントが平均から広く散らばっていることを示す。
- 標準偏差 (Standard Deviation): 分散の平方根として計算され、データのばらつきをより直感的に理解するために使用される。
計算方法
数式での表現:
- 分散:
\[ \text{分散} = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2 \]
ここで、\( x_i \) は各データポイント、\( \bar{x} \) は平均値、\( n \) はデータの個数です。 - 標準偏差:
\[ \text{標準偏差} = \sqrt{\text{分散}} \]
実例と解釈
以下のPythonコードは、サンプルデータの分散と標準偏差を計算する例です。
import numpy as np
# Sample Data: Test scores of 5 students
scores = [80, 90, 85, 92, 88]
# Calculating the variance and standard deviation
variance = np.var(scores)
std_dev = np.std(scores)
print(f"The variance of test scores is: {variance}")
print(f"The standard deviation of test scores is: {std_dev}")The variance of test scores is: 17.6
The standard deviation of test scores is: 4.1952353926806065このコードを実行すると、テストスコアの分散と標準偏差が出力されます。標準偏差は、データのばらつきの大きさを示す指標として解釈できます。例えば、標準偏差が大きければ、生徒のテストのスコアは平均から広く散らばっていることを意味します。
また、以下のPythonコードは、テストスコアとその平均値、そして1つの標準偏差の範囲を棒グラフで示しています。
import matplotlib.pyplot as plt
# Data
students = ['A', 'B', 'C', 'D', 'E']
# Mean calculation
mean_score = np.mean(scores)
# Creating bar plot
plt.bar(students, scores, color='blue')
plt.axhline(y=mean_score, color='r', linestyle='-')
plt.axhline(y=mean_score + std_dev, color='g', linestyle='--')
plt.axhline(y=mean_score - std_dev, color='g', linestyle='--')
# Adding labels and title
plt.xlabel("Students")
plt.ylabel("Scores")
plt.title("Test Scores of 5 Students with Mean and Standard Deviation Lines")
plt.text(4.5,mean_score + 1, 'Mean', color = 'red')
plt.text(4.5,mean_score + std_dev + 1, '+1 Std Dev', color = 'green')
plt.text(4.5,mean_score - std_dev - 1, '-1 Std Dev', color = 'green')
# Display the plot
plt.show()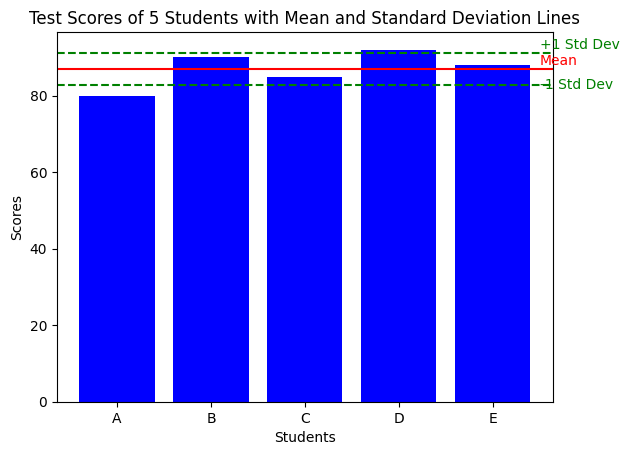
このグラフでは、赤い線が平均値を示し、緑の破線が1つの標準偏差の範囲を示しています。これにより、テストスコアが平均値と比較してどのように分布しているかが視覚的に理解しやすくなっています。
標準化変量
定義と目的
標準化変量(またはzスコア)は、個々のデータポイントが平均からどれだけ離れているかを、標準偏差の単位で示す統計量です。これにより、異なるデータセットや異なる単位のデータを共通の尺度で比較できます。標準化されたデータは、平均が0、標準偏差が1となるため、分析や機械学習モデルの入力として使用する際に役立ちます。
計算方法
数式での表現:
\[ z = \frac{x – \mu}{\sigma} \]
ここで、
- \( x \) はデータポイント
- \( \mu \) はデータセットの平均
- \( \sigma \) はデータセットの標準偏差
実例と解釈
以下のPythonコードは、サンプルデータを標準化する例です。
import numpy as np
# Sample Data: Test scores of 5 students
scores = [80, 90, 85, 92, 88]
# Calculating the mean and standard deviation
mean_score = np.mean(scores)
std_dev_score = np.std(scores)
# Standardizing the scores
z_scores = [(x - mean_score) / std_dev_score for x in scores]
print(f"Original Scores: {scores}")
print(f"Z-Scores: {z_scores}")Original Scores: [80, 90, 85, 92, 88]
Z-Scores: [-1.6685595311797865, 0.7150969419341942, -0.4767312946227961, 1.1918282365569903, 0.23836564731139806]このコードを実行すると、元のテストスコアとそれに対応するzスコアが出力されます。zスコアは、それぞれのスコアが平均スコアからどれだけ離れているかを示しています。例えば、zスコアが2の場合、そのスコアは平均よりも2つの標準偏差分高いことを意味します。
また、以下のPythonコードは、元のテストスコアとそのzスコアを散布図で比較しています。
import matplotlib.pyplot as plt
# Creating a scatter plot
plt.scatter(scores, [1]*len(scores), color='blue', label='Original Scores')
plt.scatter(z_scores, [2]*len(z_scores), color='red', label='Z-Scores')
# Adding labels and title
plt.yticks([1,2], ['Original Scores', 'Z-Scores'])
plt.title("Comparison of Original Scores and Z-Scores")
plt.xlabel("Scores")
plt.legend()
# Display the plot
plt.show()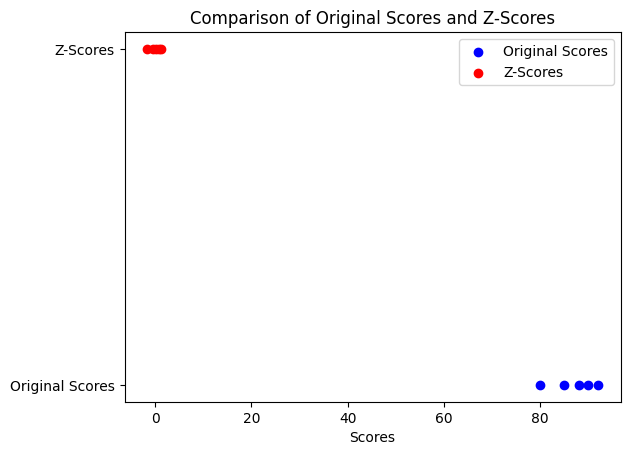
このグラフでは、元のテストスコア(青色)とzスコア(赤色)がどのように関連しているかを比較しています。zスコアは、元のスコアを標準化したものであるため、その分布の形状は元のスコアと同じですが、平均が0になり、標準偏差が1になるように変換されています。
偏差値
定義と目的
偏差値は、あるデータがそのデータセットの中でどれだけ優れているか、劣っているかを示す指標です。具体的には、平均値を50、標準偏差を10とした標準化変量です。偏差値は主に試験の結果や能力テストのスコアなどを比較・評価する際に利用されます。偏差値が高いほど、そのスコアは平均よりも高いことを示し、偏差値が低いほど平均よりも低いことを示します。
計算方法
数式での表現:
\[
\text{偏差値} = 50 + 10 \times \frac{x – \mu}{\sigma}
\]
ここで、
- \( x \) はデータポイント
- \( \mu \) はデータセットの平均
- \( \sigma \) はデータセットの標準偏差
実例と解釈
以下のPythonコードは、サンプルデータの偏差値を計算する例です。
import numpy as np
# Sample Data: Test scores of 5 students
scores = [80, 90, 85, 92, 88]
# Calculating the mean and standard deviation
mean_score = np.mean(scores)
std_dev_score = np.std(scores)
# Calculating the deviation values
deviation_values = [50 + 10 * (x - mean_score) / std_dev_score for x in scores]
print(f"Original Scores: {scores}")
print(f"Deviation Values: {deviation_values}")Original Scores: [80, 90, 85, 92, 88]
Deviation Values: [33.31440468820213, 57.15096941934194, 45.23268705377204, 61.9182823655699, 52.38365647311398]このコードを実行すると、元のテストスコアとそれに対応する偏差値が出力されます。偏差値は、それぞれのスコアがデータセット全体の中でどれだけ優れているか、劣っているかを示しています。例えば、偏差値が60の場合、そのスコアは平均よりも1つの標準偏差分高いことを意味します。
また、以下のPythonコードは、元のテストスコアとその偏差値を散布図で比較しています。
import matplotlib.pyplot as plt
# Creating a scatter plot
plt.scatter(scores, [1]*len(scores), color='blue', label='Original Scores')
plt.scatter(deviation_values, [2]*len(deviation_values), color='red', label='Deviation Values')
# Adding labels and title
plt.yticks([1,2], ['Original Scores', 'Deviation Values'])
plt.title("Comparison of Original Scores and Deviation Values")
plt.xlabel("Scores/Values")
plt.legend()
# Display the plot
plt.show()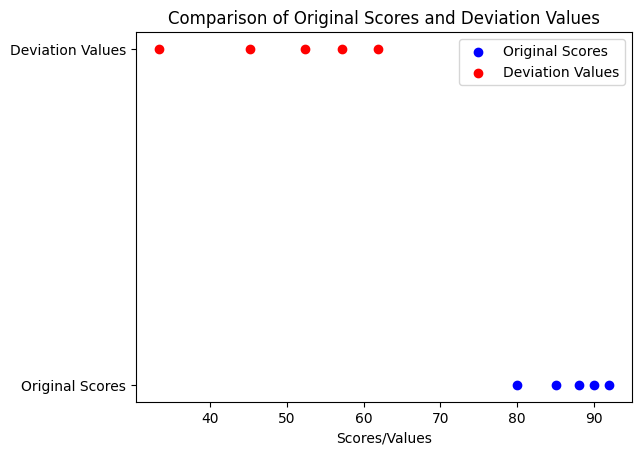
このグラフでは、元のテストスコア(青色)と偏差値(赤色)がどのように関連しているかを比較しています。偏差値は、元のスコアを特定の方法で標準化したものであるため、その分布の形状は元のスコアと同じですが、平均が50、標準偏差が10になるように変換されています。
変動係数
定義と目的
変動係数(Coefficient of Variation: CV)は、データセットの標準偏差を平均で割った値です。変動係数は、異なる単位や範囲を持つデータセットの変動やばらつきを比較する際に使用されます。この指標は、データセットのばらつきが平均に対してどれほど大きいかを示すパーセンテージとして表現されます。変動係数が大きいほど、データのばらつきが大きいことを示します。
計算方法
数式での表現:
\[
CV = \left( \frac{\sigma}{\mu} \right) \times 100
\]
ここで、
- \( \sigma \) はデータセットの標準偏差
- \( \mu \) はデータセットの平均
実例と解釈
以下のPythonコードは、2つのサンプルデータセットの変動係数を計算する例です。
import numpy as np
# Sample Data
dataset_A = [50, 55, 53, 54, 52]
dataset_B = [100, 110, 105, 107, 108]
# Calculating the Coefficient of Variation
CV_A = (np.std(dataset_A) / np.mean(dataset_A)) * 100
CV_B = (np.std(dataset_B) / np.mean(dataset_B)) * 100
print(f"Coefficient of Variation for Dataset A: {CV_A:.2f}%")
print(f"Coefficient of Variation for Dataset B: {CV_B:.2f}%")Coefficient of Variation for Dataset A: 3.26%
Coefficient of Variation for Dataset B: 3.21%このコードを実行すると、2つのデータセットの変動係数が出力されます。変動係数の値に基づき、どちらのデータセットのばらつきが大きいかを判断できます。
また、以下のPythonコードは、元のデータセットとその変動係数を棒グラフで比較しています。
import matplotlib.pyplot as plt
# Bar graph representation
labels = ['Dataset A', 'Dataset B']
CV_values = [CV_A, CV_B]
plt.bar(labels, CV_values, color=['blue', 'red'])
# Adding labels and title
plt.ylabel('Coefficient of Variation (%)')
plt.title('Comparison of Coefficient of Variation')
plt.ylim(0, max(CV_values) + 5) # Adjusting y-axis limits for better visualization
# Display the plot
plt.show()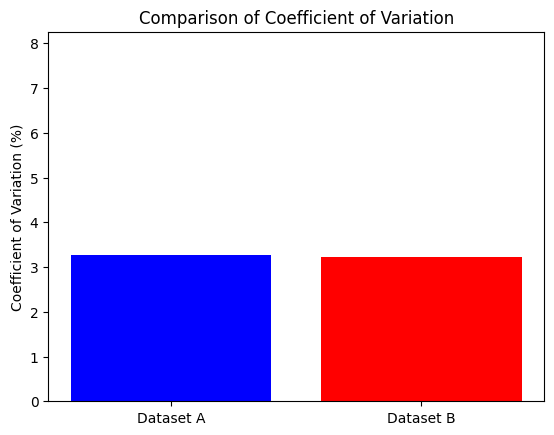
このグラフでは、2つのデータセットの変動係数を比較しています。変動係数が高いデータセットは、そのデータセットのばらつきが相対的に大きいことを示しています。
共分散
定義と目的
共分散(Covariance)は、2つの変数の関係を示す統計的指標であり、一方の変数が平均からどれだけ逸脱すると、もう一方の変数がどれだけ逸脱するかを示します。共分散の値が正の場合、一方の変数が増加するともう一方の変数も増加する傾向があります。逆に、共分散の値が負の場合、一方の変数が増加するともう一方の変数が減少する傾向があります。
計算方法
2つの変数、\( X \) と \( Y \) の共分散は以下の式で表されます。
\[
\text{Cov}(X, Y) = \frac{1}{n}\sum_{i=1}^{n}(X_i – \bar{X})(Y_i – \bar{Y})
\]
ここで、
- \( n \) はデータの数
- \( X_i \) と \( Y_i \) は各データポイント
- \( \bar{X} \) と \( \bar{Y} \) はそれぞれの変数の平均値
実例と解釈
以下のPythonコードは、2つのサンプルデータセットの共分散を計算する例です。
import numpy as np
# Sample Data
X = [10, 20, 30, 40, 50]
Y = [5, 15, 25, 35, 45]
# Calculating the covariance
cov_matrix = np.cov(X, Y, bias=True)
cov_value = cov_matrix[0, 1]
print(f"Covariance between X and Y: {cov_value:.2f}")Covariance between X and Y: 200.00このコードを実行すると、データセット\( X \) と \( Y \) の間の共分散の値が出力されます。この共分散の値を解釈することで、2つのデータセット間の関係の強さと方向を評価できます。ただし、共分散の値は変数の単位に依存するため、相関係数を使用して正規化することが一般的です。
また、以下のPythonコードは、元のデータセットを散布図で表示しています。
import matplotlib.pyplot as plt
# Scatter plot representation
plt.scatter(X, Y, color='blue', label='Data points')
# Adding labels and title
plt.xlabel('X values')
plt.ylabel('Y values')
plt.title('Scatter plot of X and Y')
plt.legend()
# Display the plot
plt.grid(True)
plt.show()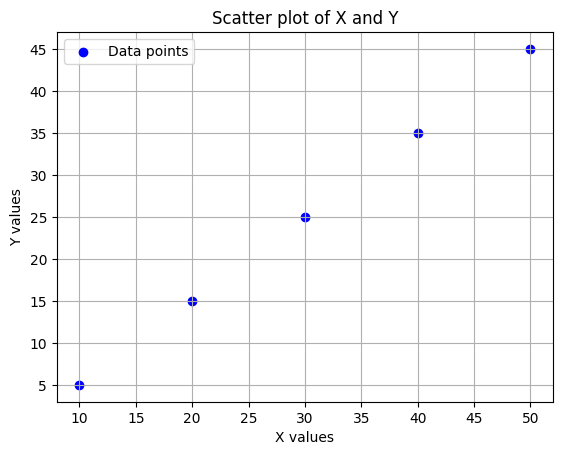
この散布図は、2つの変数間の関係を視覚的に評価するのに役立ちます。共分散の正または負の値は、散布図の傾きの方向と一致するはずです。
相関係数
定義と目的
相関係数(Correlation Coefficient)は、二つの変数の間の線形的な関係の強さと方向を示す統計的指標です。相関係数は -1 から 1 の範囲で、1 は完全な正の線形関係、-1 は完全な負の線形関係、0 は線形関係がないことを示します。相関係数を使うことで、二つの変数間の関連性を量的に評価できます。
計算方法
ピアソンの積率相関係数は以下の式で表されます。
\[
r_{XY} = \frac{\sum_{i=1}^{n} (X_i – \bar{X})(Y_i – \bar{Y})}{\sqrt{\sum_{i=1}^{n} (X_i – \bar{X})^2} \sqrt{\sum_{i=1}^{n} (Y_i – \bar{Y})^2}}
\]
ここで、
- \( n \) はデータの数
- \( X_i \) と \( Y_i \) は各データポイント
- \( \bar{X} \) と \( \bar{Y} \) はそれぞれの変数の平均値
実例と解釈
以下のPythonコードは、2つのサンプルデータセットの相関係数を計算する例です。
import numpy as np
# Sample Data
X = [10, 20, 30, 40, 50]
Y = [5, 15, 25, 35, 45]
# Calculating the correlation coefficient
corr_coeff = np.corrcoef(X, Y)[0, 1]
print(f"Correlation coefficient between X and Y: {corr_coeff:.2f}")Correlation coefficient between X and Y: 1.00
このコードを実行すると、データセット\( X \) と \( Y \) の間の相関係数の値が出力されます。この相関係数の値を解釈することで、2つのデータセット間の関係の強さと方向を評価できます。
また、以下のPythonコードは、元のデータセットを散布図で表示しています。
import matplotlib.pyplot as plt
# Scatter plot representation
plt.scatter(X, Y, color='blue', label='Data points')
# Adding labels and title
plt.xlabel('X values')
plt.ylabel('Y values')
plt.title('Scatter plot of X and Y')
plt.legend()
# Display the plot
plt.grid(True)
plt.show()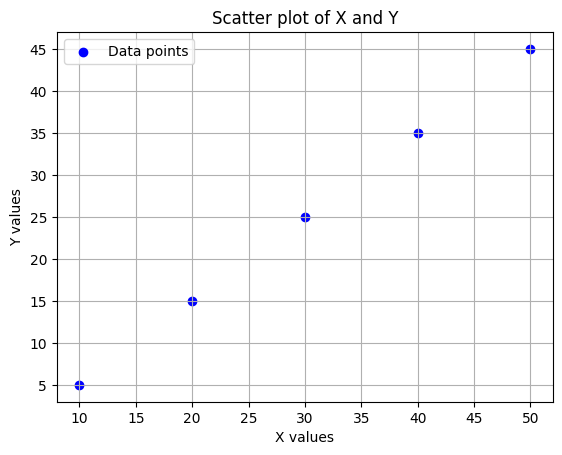
この散布図は、2つの変数間の関係を視覚的に評価するのに役立ちます。相関係数の正または負の値は、散布図の傾きの方向と一致するはずです。
まとめ
データ分析の基本的なステップをマスターすることは、情報の海の中で意味のある洞察を得るための鍵です。ここでは、データの客観的な分析のための重要な統計的概念と方法について学びました。
- 平均値:データセットの中心を示す基本的な指標。
- 分散と標準偏差:データのばらつきや散らばり具合を示す指標。
- 標準化変量:異なる尺度のデータを共通の尺度に変換する方法。
- 偏差値:あるデータが集団の中でどれだけ優れているか、劣っているかを示す指標。
- 変動係数:データの散らばり具合を相対的に評価する方法。
- 共分散:2つの変数が同時にどのように動くかを示す指標。
- 相関係数:2つの変数の間の線形的な関係の強さを示す指標。
これらの概念と方法を理解することで、データを正確に解釈し、意味のある洞察を導き出す能力が向上します。しかし、これらのツールは単に始点に過ぎません。実際のデータ分析のプロジェクトでは、これらの基本的な概念を応用して、より複雑な分析やモデリングを行う必要があります。
Pythonを使用することで、これらの統計的概念を簡単に計算し、データを視覚化できます。Pythonの強力なライブラリとツールキットを活用することで、効率的で正確なデータ分析が実現します。

▼AIを使った副業・起業アイデアを紹介♪
