※本サイトはプロモーションが含まれています。記事内容は公平さを心がけています。

正規分布で将来を予測 | データサイエンティスト 統計学の基礎

データサイエンティストの必須知識、「正規分布で将来を予測 | 統計学の基礎」について解説します。

正規分布の基礎

正規分布

正規分布は、統計学や確率論でとてもよく使われる確率分布の1つです。自然界や社会現象の多くが正規分布に従っているため、「ガウス分布」とも呼ばれます。

正規分布の定義

正規分布は、以下の確率密度関数で表されます。

\[
f(x) = \frac{1}{{\sqrt{2\pi\sigma^2}}} \exp\left(-\frac{{(x-\mu)^2}}{{2\sigma^2}}\right)
\]

ここで、
\(\mu\) は平均（期待値）,
\(\sigma\) は標準偏差を示します。

正規分布の特徴

  • ベルカーブとも呼ばれる、対称な形をしています。
  • 平均 \(\mu\) を中心に、データが集まっています。
  • 標準偏差 \(\sigma\) は、データの散らばり具合を示します。大きいほど分布は広がり、小さいほど狭くなります。

正規分布の実例

Pythonでの可視化

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 平均と標準偏差を設定
mu = 0
sigma = 1

# x軸の値
x = np.linspace(-5, 5, 1000)

# 正規分布の確率密度関数を計算
y = norm.pdf(x, mu, sigma)

plt.plot(x, y)
plt.title("Standard Normal Distribution")
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.grid(True)
plt.show()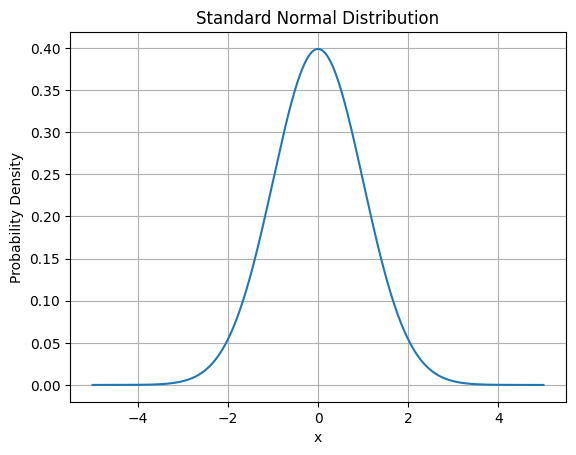
平均0、標準偏差1の正規分布

このグラフは、平均0、標準偏差1の正規分布を示しています。多くの実際のデータがこの分布に似た形をとるため、正規分布はとても重要です。

確率分布の期待値と標準偏差

確率分布は、ランダムな変数の取りうる各値とその確率を表します。確率分布の中心的な性質である期待値と標準偏差について解説します。

期待値の定義

期待値は、確率分布の「平均」または「中心」と考えることができます。確率変数\(X\)の期待値\(E(X)\)は以下の式で計算されます。

\[
E(X) = \sum x \cdot P(X = x)
\]

ここで、\(P(X = x)\)は確率変数\(X\)が値\(x\)をとる確率を意味します。

標準偏差の定義

標準偏差は、確率分布の「散らばり」を表す指標です。確率変数\(X\)の標準偏差\(\sigma(X)\)は以下の式で計算されます。

\[
\sigma(X) = \sqrt{E(X^2) – (E(X))^2}
\]

期待値と標準偏差の関係

期待値は確率分布の中心を、標準偏差はその散らばりを示します。正規分布の場合、期待値は分布のピークを示し、標準偏差はその幅を示します。

Pythonでの例

以下は、期待値と標準偏差を計算するPythonのコード例です。

import numpy as np

# 例として、サイコロの目の分布を考える
values = np.array([1, 2, 3, 4, 5, 6])
probabilities = np.array([1/6, 1/6, 1/6, 1/6, 1/6, 1/6])

# 期待値
expected_value = np.sum(values * probabilities)

# 標準偏差
variance = np.sum(probabilities * (values - expected_value)**2)
standard_deviation = np.sqrt(variance)

print(f"Expected Value: {expected_value}")
print(f"Standard Deviation: {standard_deviation}")
Expected Value: 3.5
Standard Deviation: 1.707825127659933

このコードは、サイコロの目の期待値と標準偏差を計算します。期待値は3.5、標準偏差は約1.71となります。

標準正規分布

標準正規分布は、正規分布の一種であり、期待値が0、標準偏差が1の特性を持っています。これは、正規分布のデータを特定の方法で変換して得られる分布です。

標準正規分布とは?

標準正規分布は、平均が0、標準偏差が1である正規分布のことを指します。数学的には、以下の確率密度関数で表されます。

\[
f(z) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} z^2}
\]

ここで、\( z \)は標準化された変数です。

標準化のプロセス

任意の正規分布を標準正規分布に変換するためには「標準化」を行います。具体的には、元のデータから平均を引き、標準偏差で割ることで標準化されます。

数式で表すと、以下のようになります。

\[
z = \frac{X – \mu}{\sigma}
\]

ここで、
\( X \) : 元のデータ
\( \mu \) : 平均
\( \sigma \) : 標準偏差

Pythonでの例

以下は、データを標準化するPythonのコード例です。

import numpy as np

# サンプルデータ
data = np.array([50, 60, 70, 80, 90])

# 平均と標準偏差を計算
mean = np.mean(data)
std_dev = np.std(data)

# 標準化
standardized_data = (data - mean) / std_dev

print(f"Standardized Data: {standardized_data}")
Standardized Data: [-1.41421356 -0.70710678  0.          0.70710678  1.41421356]

標準正規分布の利用例

標準正規分布は、さまざまな場面で利用されます。例えば、テストのスコアの分布や身長の分布など、自然界の多くの現象は正規分布に従うとされています。標準正規分布を使用すると、特定のスコアが全体の何パーセンタイルに位置するのか、あるいは特定のスコア以上を取得する確率などを簡単に計算できます。

例: あるテストのスコアが平均70点、標準偏差10点の正規分布に従うとする。80点以上を取得する確率を求める場合、まず80点を標準正規分布に標準化し、その後、標準正規分布表を使用して確率を求めることができます。

標準正規分布表

標準正規分布表は、標準正規分布に従う確率変数の確率を簡単に求めるための表です。この表を使用することで、特定のスコアや値以下の確率を素早く計算できます。

以下は、Pythonによる標準正規分布表を作成する簡単な例です。

import numpy as np
from scipy.stats import norm

# zスコアの範囲を設定
z_scores = np.arange(-3.5, 3.6, 0.1)

# 確率を計算
probabilities = [norm.cdf(z) for z in z_scores]

# 表を表示
for z, p in zip(z_scores, probabilities):
    print(f"z = {z:.2f}: P(Z <= {z:.2f}) = {p:.4f}")
z = -2.20: P(Z <= -2.20) = 0.0139
z = -2.10: P(Z <= -2.10) = 0.0179
z = -2.00: P(Z <= -2.00) = 0.0228
z = -1.90: P(Z <= -1.90) = 0.0287
z = -1.80: P(Z <= -1.80) = 0.0359
z = -1.70: P(Z <= -1.70) = 0.0446
z = -1.60: P(Z <= -1.60) = 0.0548
z = -1.50: P(Z <= -1.50) = 0.0668
z = -1.40: P(Z <= -1.40) = 0.0808
z = -1.30: P(Z <= -1.30) = 0.0968
z = -1.20: P(Z <= -1.20) = 0.1151
z = -1.10: P(Z <= -1.10) = 0.1357
z = -1.00: P(Z <= -1.00) = 0.1587
z = -0.90: P(Z <= -0.90) = 0.1841
z = -0.80: P(Z <= -0.80) = 0.2119
z = -0.70: P(Z <= -0.70) = 0.2420
z = -0.60: P(Z <= -0.60) = 0.2743
z = -0.50: P(Z <= -0.50) = 0.3085
z = -0.40: P(Z <= -0.40) = 0.3446
z = -0.30: P(Z <= -0.30) = 0.3821
z = -0.20: P(Z <= -0.20) = 0.4207
z = -0.10: P(Z <= -0.10) = 0.4602
z = 0.00: P(Z <= 0.00) = 0.5000
z = 0.10: P(Z <= 0.10) = 0.5398
z = 0.20: P(Z <= 0.20) = 0.5793
z = 0.30: P(Z <= 0.30) = 0.6179
z = 0.40: P(Z <= 0.40) = 0.6554
z = 0.50: P(Z <= 0.50) = 0.6915
z = 0.60: P(Z <= 0.60) = 0.7257
z = 0.70: P(Z <= 0.70) = 0.7580
z = 0.80: P(Z <= 0.80) = 0.7881
z = 0.90: P(Z <= 0.90) = 0.8159
z = 1.00: P(Z <= 1.00) = 0.8413
z = 1.10: P(Z <= 1.10) = 0.8643
z = 1.20: P(Z <= 1.20) = 0.8849
z = 1.30: P(Z <= 1.30) = 0.9032
z = 1.40: P(Z <= 1.40) = 0.9192
z = 1.50: P(Z <= 1.50) = 0.9332
z = 1.60: P(Z <= 1.60) = 0.9452
z = 1.70: P(Z <= 1.70) = 0.9554
z = 1.80: P(Z <= 1.80) = 0.9641
z = 1.90: P(Z <= 1.90) = 0.9713
z = 2.00: P(Z <= 2.00) = 0.9772
z = 2.10: P(Z <= 2.10) = 0.9821
z = 2.20: P(Z <= 2.20) = 0.9861
z = 2.30: P(Z <= 2.30) = 0.9893
z = 2.40: P(Z <= 2.40) = 0.9918
z = 2.50: P(Z <= 2.50) = 0.9938
z = 2.60: P(Z <= 2.60) = 0.9953
z = 2.70: P(Z <= 2.70) = 0.9965
z = 2.80: P(Z <= 2.80) = 0.9974
z = 2.90: P(Z <= 2.90) = 0.9981
z = 3.00: P(Z <= 3.00) = 0.9987
z = 3.10: P(Z <= 3.10) = 0.9990
z = 3.20: P(Z <= 3.20) = 0.9993
z = 3.30: P(Z <= 3.30) = 0.9995
z = 3.40: P(Z <= 3.40) = 0.9997
z = 3.50: P(Z <= 3.50) = 0.9998

このコードは、zスコアが-3.5から3.5の範囲で、0.1刻みで変化する場合の標準正規分布の累積確率を表示します。

注意: 実際の標準正規分布表はより詳細で、0.01刻みなどの細かいzスコアの間隔で確率を提供することが多いです。必要に応じて、上記のコードのz_scoresの範囲や間隔を調整してください。

標準正規分布表の読み方

  1. 標準正規分布表は、\( z \)スコアとそれに対応する確率が一覧になっています。
  2. 表の左側の列が\( z \)スコアの整数部分と小数部分の最初の1桁、上部の行が小数部分の2桁目を示しています。
  3. これらの値を組み合わせることで、具体的な\( z \)スコアに対応する確率を読み取ることができます。

確率の計算方法

標準正規分布表を使用して、特定の\( z \)スコア以下の確率を求める方法を示します。

  1. まず、求めたい\( z \)スコアを特定します。
  2. 表を参照して、その\( z \)スコアに対応する確率を見つけます。
  3. この確率は、求めたい\( z \)スコア以下の範囲に含まれる確率を示しています。

実例: 標準正規分布表を使った問題

問題: \( z \)スコアが1.65の場合、このスコア以下のデータの確率は何%ですか？

解答:
標準正規分布表を参照すると、\( z = 1.65 \)の確率は約0.9505または95.05%です。

Pythonでの例

PythonのSciPyライブラリを使用して、この確率を計算することもできます。

from scipy.stats import norm

# zスコア
z_score = 1.65

# 確率の計算
probability = norm.cdf(z_score)

print(f"The probability for z = {z_score} is approximately {probability:.4f} or {probability*100:.2f}%.")
The probability for z = 1.65 is approximately 0.9505 or 95.05%.

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


前の記事

推測統計学と記述統計学、確率 | データサイエンティスト 統計…

次の記事

標本から母集団を推定する | データサイエンティスト 統計学の…