標本から母集団を推定する | データサイエンティスト 統計学の基礎

データサイエンティストの必須知識、「標本から母集団を推定する | 統計学の基礎」について解説します。

母集団の未知な値（母数）を標本から推定する

推定の基礎

推定とは?

推定は、得られた標本データから、母集団の未知のパラメータ（平均、分散など）を予測する方法を指します。例えば、ある商品の満足度を調査する際、全員からの意見を聞くのは難しいため、一部の人々から意見を聞き全体の意見を推定します。

パラメータと統計量

• パラメータ: 母集団の特性を表す数値。例: 母平均、母分散
• 統計量: 標本データから計算される数値。この数値を使用してパラメータを推定する。例: 標本平均、標本分散

import numpy as np

# 標本データ
sample_data = [2, 3, 4, 5, 6]

# 標本平均
sample_mean = np.mean(sample_data)
# 標本分散
sample_variance = np.var(sample_data)

print(f"Sample mean: {sample_mean}")
print(f"Sample variance: {sample_variance}")

Sample mean: 4.0
Sample variance: 2.0

点推定と区間推定

• 点推定: 母集団のパラメータを1つの数値で推定する方法。例: 母平均を5と推定する。
• 区間推定: 母集団のパラメータが取りうる範囲を推定する方法。例: 母平均は4から6の間であると推定する。

import scipy.stats as stats

# 95%信頼区間の計算
confidence_level = 0.95
degrees_freedom = len(sample_data) - 1
confidence_interval = stats.t.interval(confidence_level, degrees_freedom, sample_mean, stats.sem(sample_data))

print(f"95% Confidence interval for the mean: {confidence_interval}")

95% Confidence interval for the mean: (2.036756838522439, 5.9632431614775605)

推定の方法

最尤推定法

最尤推定法は、与えられたデータに対して、ある確率モデルのパラメータの「もっともらしい」値を推定する方法です。具体的には、データが観測される尤度（確率）を最大にするパラメータの値を求めることを目的とします。

\[
\hat{\theta} = \arg\max_\theta P(D|\theta)
\]

ここで、\( \hat{\theta} \) は推定されたパラメータ、\( P(D|\theta) \) はデータ \( D \) が観測される確率を表します。

import numpy as np
from scipy.optimize import minimize

# サンプルデータ
data = np.array([2, 3, 4, 5, 6])

# 尤度関数（正規分布を仮定）
def negative_likelihood(params):
    mu, sigma = params
    return -np.sum(np.log(stats.norm.pdf(data, mu, sigma)))

# 最尤推定
initial_guess = [np.mean(data), np.std(data)]
result = minimize(negative_likelihood, initial_guess)
mu_mle, sigma_mle = result.x

print(f"MLE of mu: {mu_mle}")
print(f"MLE of sigma: {sigma_mle}")

MLE of mu: 4.0
MLE of sigma: 1.4142135623730951

モーメント法

モーメント法は、標本のモーメント（平均、分散など）を使用して、母集団のパラメータを推定する方法です。例えば、標本平均を用いて母平均を、標本分散を用いて母分散を推定できます。

\[
\mu = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
\[
\sigma^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i – \mu)^2
\]

ベイズ推定

ベイズ推定は、事前の知識（事前分布）と新たに得られたデータを組み合わせて、パラメータの事後分布を求める方法です。事後分布は、新しいデータが与えられたときのパラメータの分布を示しています。

\[
P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}
\]

ここで、\( P(\theta|D) \) は事後分布、\( P(D|\theta) \) は尤度、\( P(\theta) \) は事前分布、\( P(D) \) はデータの確率を表します。

ベイズ推定の利点は、事前の知識を内包できる点です。しかし、事前分布の選択や計算の複雑さが課題となることもあります。

標本統計量と標本分布

標本統計量の定義

標本統計量は、標本データから計算される数値で、母集団の特性や性質を推測するための情報を提供します。具体的には、標本平均や標本分散などがこれに当たります。

\[
\text{標本平均} = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
\[
\text{標本分散} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i – \bar{x})^2
\]

ここで、\( x_i \) は標本データ、\( n \) は標本のサイズ、\( \bar{x} \) は標本平均を示します。

標本分布の概念

標本分布とは、ある標本統計量が取りうるすべての値とその確率の分布を指します。例えば、標本平均の標本分布は、異なる標本から計算される標本平均の分布を示すものです。

import numpy as np
import matplotlib.pyplot as plt

# 母集団: 平均50, 標準偏差10の正規分布
population = np.random.normal(50, 10, 10000)

# 標本平均の分布を計算
sample_means = [np.mean(np.random.choice(population, 30)) for _ in range(1000)]

# ヒストグラムで標本平均の分布を表示
plt.hist(sample_means, bins=50, edgecolor='k', alpha=0.7)
plt.title("Distribution of Sample Means")
plt.xlabel("Sample Mean")
plt.ylabel("Frequency")
plt.show()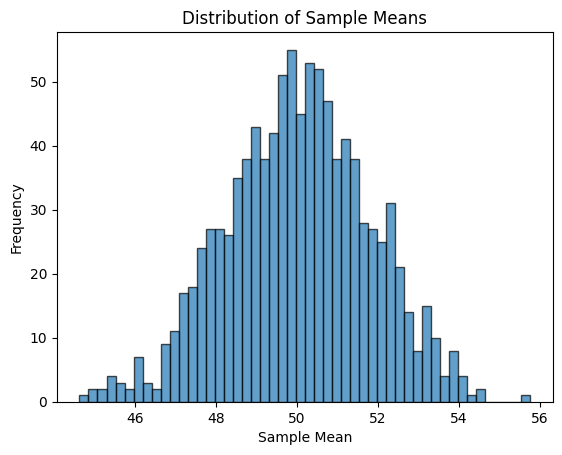

大数の法則

大数の法則は、標本のサイズが大きくなるにつれて、標本平均や他の標本統計量が母集団の真の値に収束するという法則です。この法則により、大きなサイズの標本を持っていれば、それに基づいて得られる統計的推定はより信頼性が高くなります。

\[
\bar{X}_n \to \mu \quad (n \to \infty)
\]

ここで、\( \bar{X}_n \) は標本平均、\( \mu \) は母平均、\( n \) は標本のサイズを示します。

中心極限定理

中心極限定理の概要

中心極限定理（CLT）は、統計学における最も重要な定理の一つです。CLTは、ある条件下で、大きなサンプルサイズの場合、多くの確率分布（特に平均と分散が有限である分布）に基づく標本平均の分布が正規分布に近づくというものです。

具体的には、任意の確率分布から独立に取られたサンプルの平均が、サンプルサイズが大きくなるにつれて正規分布に従うようになります。

数式で表すと以下のようになります。
\[
\bar{X}_n \approx N\left(\mu, \frac{\sigma^2}{n}\right)
\]
ここで、\( \bar{X}_n \) は標本平均、\( \mu \) は母平均、\( \sigma^2 \) は母分散、\( n \) は標本のサイズを示します。

応用例

中心極限定理は、母集団が非正規分布であっても、大きなサンプルサイズの下で標本平均の分布を正規分布として扱えるという利点があります。これにより、多くの統計的検定や信頼区間の推定など、正規分布を前提とした手法が使用可能となります。

import numpy as np
import matplotlib.pyplot as plt

# 母集団: 一様分布
population = np.random.uniform(0, 1, 10000)

# 標本平均の分布を計算（サンプルサイズ=30）
sample_means = [np.mean(np.random.choice(population, 30)) for _ in range(1000)]

# ヒストグラムで標本平均の分布を表示
plt.hist(sample_means, bins=50, edgecolor='k', alpha=0.7)
plt.title("Distribution of Sample Means (Uniform Distribution)")
plt.xlabel("Sample Mean")
plt.ylabel("Frequency")
plt.show()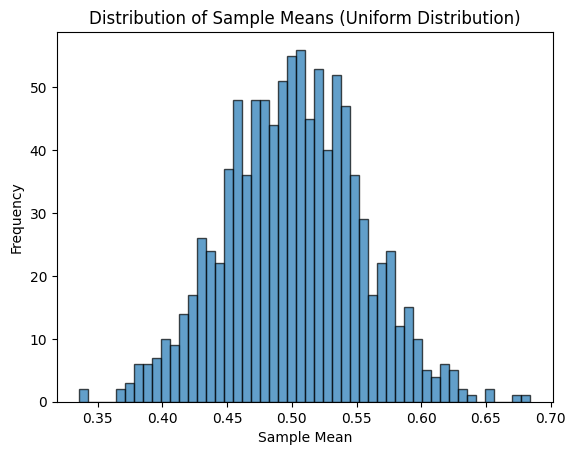

制約と注意点

中心極限定理の前提として、サンプルが独立にランダムに抽出されていること、そして母集団の平均と分散が有限であることが挙げられます。一部の分布（例えば、カオティックな分布や無限の分散を持つ分布）では、CLTが適用できない場合があります。

また、標本のサイズが「大きい」とは一般的に30以上を意味しますが、元の分布の形によっては、より大きなサンプルサイズが必要となる場合もあります。

良い推定量の特性

不偏性

不偏性とは、推定量の期待値が真のパラメータと一致する性質を指します。言い換えると、推定量が系統的な誤差を持たないことを意味します。数学的には以下のように表されます。

\[
E[\hat{\theta}] = \theta
\]

ここで、\( \hat{\theta} \) は推定量、\( \theta \) は真のパラメータ、\( E[] \) は期待値を示します。

例えば、標本平均は母平均の不偏推定量であると言えます。一方、標本分散の分子は \( n \) ではなく \( n-1 \) で割ることで不偏性を持つように調整されています。

一致性

一致性とは、標本のサイズが増えるにつれて、推定量が真のパラメータに収束する性質を指します。数学的には以下のように表されます。

\[
\lim_{n \to \infty} P(|\hat{\theta}_n – \theta| > \epsilon) = 0
\]

すべての \( \epsilon > 0 \) に対して上の式が成り立つ場合、推定量 \( \hat{\theta}_n \) は一致推定量であると言います。

有効性

有効性とは、ある推定量が他の不偏推定量よりも小さな分散を持つことを意味します。もし推定量 \( \hat{\theta}_1 \) が推定量 \( \hat{\theta}_2 \) よりも小さい分散を持ち、両方とも不偏であるならば、\( \hat{\theta}_1 \) は \( \hat{\theta}_2 \) よりも有効であると言います。

数式で示すと、以下のようになります。

\[
Var(\hat{\theta}_1) < Var(\hat{\theta}_2)
\]

ここで、\( Var() \) は分散を示します。

標本の分散と標準偏差

標本分散の定義

標本分散は、データの散らばり具合を示す統計量として利用されます。標本分散 \( s^2 \) は次のように計算されます。

\[
s^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2
\]

ここで、
\( x_i \) : データの各値
\( \bar{x} \) : データの平均値
\( n \) : データの数

不偏分散とその重要性

不偏分散は、母集団の分散を推定するための統計量として用いられます。標本分散の計算では分母が \( n \) でしたが、不偏分散では分母が \( n-1 \) となります。不偏分散 \( s^2_u \) は以下のように計算されます。

\[
s^2_u = \frac{1}{n-1}\sum_{i=1}^{n}(x_i – \bar{x})^2
\]

不偏分散の重要性は、母集団の真の分散を無偏に推定できる点にあります。具体的には、標本から計算される分散が系統的に真の分散を過小評価する傾向があるため、分母を \( n-1 \) にすることでその偏りを補正しています。

標本標準偏差の計算方法

標本標準偏差は、分散の正の平方根として定義されます。計算式は以下のとおりです。

\[
s = \sqrt{s^2}
\]

標本標準偏差は、データの散らばり具合を直感的に理解しやすいスケールで示すための統計量として利用されます。

以下は、Pythonコードを使用して、標本分散、不偏分散、および標本標準偏差を計算する例です。

import numpy as np

# Sample data
data = np.array([5, 7, 9, 10, 12])

# Sample variance
sample_variance = np.var(data)

# Unbiased variance
unbiased_variance = np.var(data, ddof=1)

# Sample standard deviation
sample_std_dev = np.std(data)

print("Sample Variance:", sample_variance)
print("Unbiased Variance:", unbiased_variance)
print("Sample Standard Deviation:", sample_std_dev)

Sample Variance: 5.84
Unbiased Variance: 7.3
Sample Standard Deviation: 2.4166091947189146

このコードを実行すると、指定されたデータセットに対する標本分散、不偏分散、および標本標準偏差が計算され、結果が表示されます。

IT起業家

▼IT人材は2030年に国内で79万人, 全世界で「8,500万人」以上不足！
▼世界の平均年収はなんと「1,000万円」以上！
▼自宅 + パソコン + 無料翻訳ツールで「全世界が仕事場！」