ロジスティック回帰の基礎
定義と概要
ロジスティック回帰は、二項分類の問題を解くための統計的手法の一つです。出力として確率を返す特徴を持ち、その確率がある閾値(例えば0.5)を超えた場合には「1」、そうでなければ「0」としてクラスを予測します。
ロジスティック回帰と線形回帰の違い
線形回帰は連続的な値を予測するのに対して、ロジスティック回帰は確率を予測します。また、ロジスティック回帰は出力を0と1の間に収めるためのシグモイド関数を使用しますが、線形回帰はそのような関数は使用しません。
ロジスティック回帰の数学的背景
シグモイド関数
シグモイド関数は、実数を0と1の間の値に変換する関数です。数式は以下の通りです。
\[
\sigma(z) = \frac{1}{1 + e^{-z}}
\]
この関数を用いることで、線形結合の結果を確率に変換します。
尤度関数
ロジスティック回帰の訓練では、実際のラベルとモデルの予測がどれだけ一致するかを測る尤度関数を最大化します。最尤推定の考え方を元に、モデルのパラメータを更新します。
ロジット変換
ロジット関数は、確率を0と1の間から、実数全体に変換する関数です。シグモイド関数の逆関数として考えることができます。
\[
\text{logit}(p) = \log\left(\frac{p}{1-p}\right)
\]
ロジスティック回帰では、このロジット変換で線形結合の結果を確率に変換します。
ロジスティック回帰の実用例
2クラス分類の例
ロジスティック回帰は2クラス分類の問題にとても適しています。具体的な例として以下のようなケースが考えられます。
- メールがスパムであるか否かを判定するスパムフィルタ
- ある病気の有無を判定する医療診断ツール
- クリックされるかされないかを予測する広告のクリック予測
- 顧客が退会するかしないかを予測する顧客離脱予測モデル
多クラス分類の例
一般的にロジスティック回帰は2クラス分類のための手法として知られていますが、多クラス分類の問題にも拡張して利用できます。具体的には、One-vs-AllやSoftmax回帰などの手法を用いて実装します。
- 手書きの数字の画像を0から9の数字に分類する手書き数字認識
- ニュース記事を政治、経済、スポーツなどのカテゴリに分類する記事カテゴリ分類
- 画像内の物体を複数のクラスに分類する物体認識タスク
ロジスティック回帰のメリット・デメリット
メリット
- 実装の容易さ: ロジスティック回帰は理解しやすく、実装も簡単です。
- 計算コストが低い: 大量のデータに対しても高速に動作します。
- 確率的出力: 予測されるクラスの確率を得られるため、予測の不確実性を評価できます。
- 特徴の重要度: 各特徴の重みを解釈しやすく、どの特徴が予測に重要であるかを知ることができます。
デメリット
- 線形性の仮定: ロジスティック回帰は基本的に線形の関係性を仮定しているため、非線形の関係性を持つデータには適していないことがあります。
- 特徴間の相互作用: 2つ以上の特徴間の相互作用を自動的に捉えることが難しい。
- 過学習: 大量の特徴を持つデータセットでは、過学習のリスクが高まる可能性があります。
- 性能: 複雑なデータセットや大規模なデータセットに対して、深層学習やアンサンブル手法などの他のアルゴリズムに比べて性能が劣ることがあります。
過学習とは?
過学習(overfitting)は、機械学習モデルが訓練データに過度に適合してしまい、新しい未知のデータ(テストデータ)に対する性能が低下してしまう現象を指します。具体的には、モデルが訓練データのノイズやランダムな変動まで学習してしまうことで発生します。
ロジスティック回帰における過学習の原因
ロジスティック回帰における過学習の主な原因は以下のとおりです。
- 特徴量の多さ: 使用する特徴量の数が多いと、モデルがそれらの特徴量を使用して訓練データに過度に適合するリスクが高まります。
- データ量の不足: 使用するデータのサンプル数が少ない場合、モデルは訓練データに過度に依存して学習しがちです。
- 複雑なモデル: パラメータが多いなど、モデルが複雑すぎると訓練データに過度に適合しやすくなります。
正則化による対策
正則化は、モデルの複雑さを制御するための手法です。ロジスティック回帰における過学習を防ぐために、L1正則化(Lasso)やL2正則化(Ridge)がよく使用されます。
L1正則化 (Lasso)
L1正則化は、モデルのコスト関数に特徴量の重みの絶対値の和を加える手法です。これにより、不要な特徴量の重みを0にでき、特徴選択の効果も期待できます。
\[
\text{コスト} = -\log(\text{尤度}) + \lambda \sum |w_i|
\]
ここで、\( \lambda \)は正則化の強度を制御するパラメータです。
L2正則化 (Ridge)
L2正則化は、モデルのコスト関数に特徴量の重みの二乗の和を加える手法です。これにより、特徴量の重みの大きさを制限し、モデルの複雑さを抑えます。
\[
\text{コスト} = -\log(\text{尤度}) + \lambda \sum w_i^2
\]
こちらも\( \lambda \)は正則化の強度を制御するパラメータです。
実際の利用シーン
ロジスティック回帰は、2クラスまたは多クラスの分類問題に対して広く使用されています。特に、確率的な出力を必要とする場合や、入力特徴量と出力の関係が線形である場合には効果的に利用できます。
業界別の利用事例
- 金融業界
クレジットスコアリング: 顧客の返済可能性を予測するためのモデルに用いられる。
不正取引検出: ある取引が不正である確率を計算するために使用される。 - 医療業界
疾患のリスク予測: 患者がある疾患を発症するリスクを計算するために用いられる。
患者の再入院リスク: 患者が再入院する可能性を予測するためのモデルに使用される。 - マーケティング
顧客の購入確率の予測: 顧客が商品を購入する確率を予測するためのモデルに使用される。
広告のクリック確率予測: ユーザが広告をクリックする確率を計算するために用いられる。
問題への適用
例: クレジットスコアリング
銀行は、ローンの申請者が返済を適切に行えるかどうかを予測するために、ロジスティック回帰を使用することがあります。この場合、入力特徴量としては、申請者の年収、職歴、他の負債の有無などが考慮され、出力は返済可能性(返済できるか、できないか)となります。
Pythonコードの例:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
# データの読み込み
data = pd.read_csv('loan_data.csv')
X = data.drop('repayment_capability', axis=1)
y = data['repayment_capability']
# 訓練データとテストデータの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ロジスティック回帰の訓練
clf = LogisticRegression()
clf.fit(X_train, y_train)
# 予測
predictions = clf.predict(X_test)
# グラフで結果を表示
plt.figure(figsize=(10, 6))
plt.scatter(np.arange(len(predictions)), predictions, color='red', label='Predictions', marker='x')
plt.scatter(np.arange(len(y_test)), y_test, color='blue', label='True Values', marker='o')
plt.legend()
plt.title("Logistic Regression Predictions vs True Values")
plt.xlabel("Sample Index")
plt.ylabel("Repayment Capability")
plt.yticks([0, 1])
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
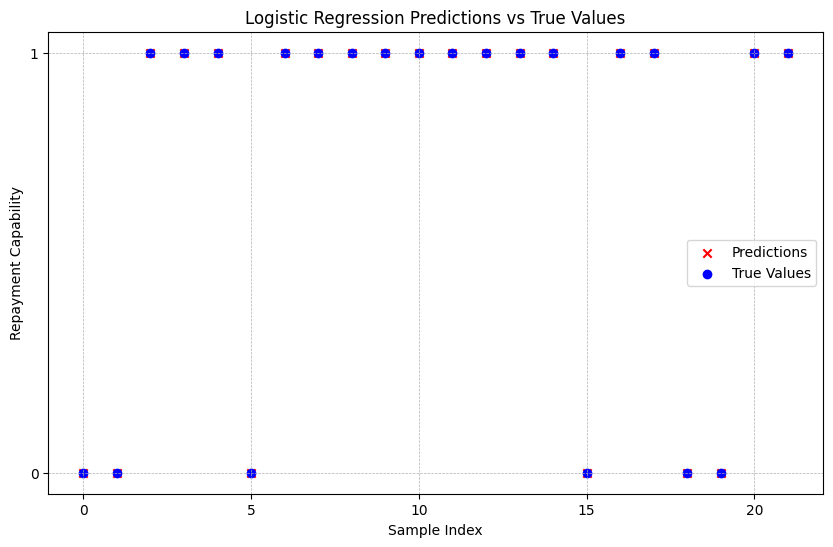
上記のコードでは、ローンのデータセット(loan_data.csv)を読み込み、ロジスティック回帰を使用して返済可能性を予測しています。
Pythonでの実装方法
必要なライブラリのインポート
ロジスティック回帰を実装するために、scikit-learnというPythonの機械学習ライブラリを利用します。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as snsデータの準備
サンプルデータとして、ある広告キャンペーンへのクリック有無(1 or 0)を予測するためのデータを考えます。
# データの読み込み
data = pd.read_csv('ad_campaign.csv')
X = data.drop('Clicked', axis=1) # クリック有無を除いた特徴量
y = data['Clicked'] # クリック有無モデルの訓練
データを訓練データとテストデータに分割し、ロジスティック回帰モデルを訓練します。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ロジスティック回帰モデルの初期化と訓練
clf = LogisticRegression()
clf.fit(X_train, y_train)予測と評価
モデルを用いて予測し、その精度を評価します。
# 予測の実施
y_pred = clf.predict(X_test)
# 精度の計算
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")モデルの可視化
ロジスティック回帰の結果を可視化するためには、係数や切片を使用して決定境界を描画する方法があります。2つの特徴量を持つデータの場合の可視化例を紹介します。
# 2つの特徴量のデータの場合の決定境界の描画
sns.scatterplot(x=X_test['Feature1'], y=X_test['Feature2'], hue=y_pred)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# 決定境界
xx, yy = np.meshgrid(np.linspace(*xlim, num=200), np.linspace(*ylim, num=200))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# 決定境界とマージンを描画
ax.contour(xx, yy, Z, colors='k', levels=[0.5], alpha=0.5, linestyles=['--'])
plt.title("Decision Boundary of Logistic Regression")
plt.show()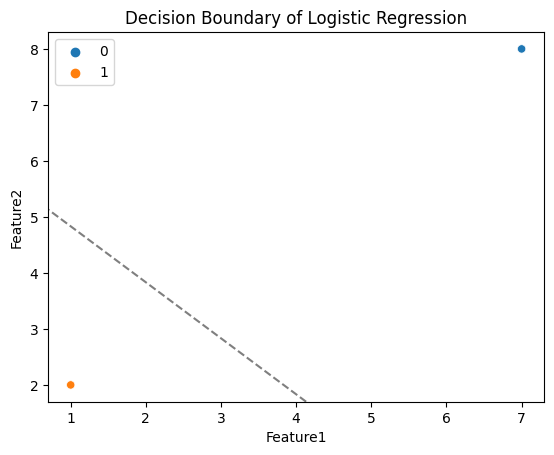
このコードは、2つの特徴量に基づいてデータポイントをプロットし、ロジスティック回帰によって生成された決定境界を示します。ロジスティック回帰モデルを使用して2つの特徴量からクリック有無を予測し、その予測性能を評価し、さらに可視化して決定境界を表示していします。これにより、モデルの性能とデータの分布を理解するのに役立ちます。
まとめ
ロジスティック回帰は、分類問題のための強力なツールであり、特に確率的な出力が必要な場合や、特徴量と出力の関係が線形であると仮定できる場合に有効です。Pythonのscikit-learnライブラリを使用することで、簡単に実装や評価が行えます。

▼AIを使った副業・起業アイデアを紹介♪
