回帰分析の基礎
回帰分析の定義
回帰分析は、変数間の関係を調査するための統計的手法の一つです。具体的には、一つの目的変数と一つ以上の説明変数の関係を数学的なモデルを使って表現します。これにより、説明変数の変動が目的変数にどのように影響するかを定量的に評価できます。
回帰分析の目的
回帰分析の主な目的は以下の通りです。
- 予測: 新しいデータが与えられたとき、目的変数の値を予測する。
- 関係の理解: 説明変数が目的変数に与える影響の大きさや方向を理解する。
- 因果関係の特定: 説明変数の変動が目的変数の変動の原因であるかを評価する(ただし、回帰分析だけで因果関係を確定することは難しい)。
主な用途と応用例
回帰分析は多岐にわたる分野で利用されています。以下はその応用例です。
- ビジネス: 売上予測、広告の効果分析、価格設定など。
- 医学: 薬の効果の評価、リスク要因の同定など。
- 経済学: 経済指標の予測、政策の影響分析など。
- 工学: 製品の品質予測、システムの性能評価など。
回帰分析の種類
単回帰分析
単回帰分析は、回帰分析の中で最も基本的な手法の一つです。この手法では、一つの目的変数と一つの説明変数の関係を数学的にモデル化します。
単回帰分析の基礎
単回帰分析の数学的なモデルは以下のように表されます。
\[ y = \beta_0 + \beta_1 x + \epsilon \]
ここで、
- \( y \) は目的変数
- \( x \) は説明変数
- \( \beta_0 \) はy切片
- \( \beta_1 \) はxの係数(傾き)
- \( \epsilon \) は誤差項
このモデルを使って、説明変数の値から目的変数の値を予測できます。また、\( \beta_1 \) の値を見ることで、説明変数が1単位増加した場合に目的変数がどれだけ変化するかを分析できます。
実際の例
広告費と売上の関係を単回帰モデルを使用してモデル化し、その結果をグラフに表示してみましょう。下記コードは広告費に基づいて売上を予測する線形モデルを訓練し、その結果を視覚的に示します。
Pythonコード:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# データセット(広告費と売上)
ad_costs = np.array([50, 100, 150, 200, 250, 300])
sales = np.array([200, 430, 650, 870, 1100, 1330])
# 単回帰モデルの訓練
model = LinearRegression().fit(ad_costs.reshape(-1, 1), sales)
# 予測
predicted_sales = model.predict(ad_costs.reshape(-1, 1))
# グラフの表示
plt.scatter(ad_costs, sales, color='blue', label='Actual Sales')
plt.plot(ad_costs, predicted_sales, color='red', label='Predicted Sales')
plt.title("Ad Costs vs Sales")
plt.xlabel("Ad Costs")
plt.ylabel("Sales")
plt.legend()
plt.show()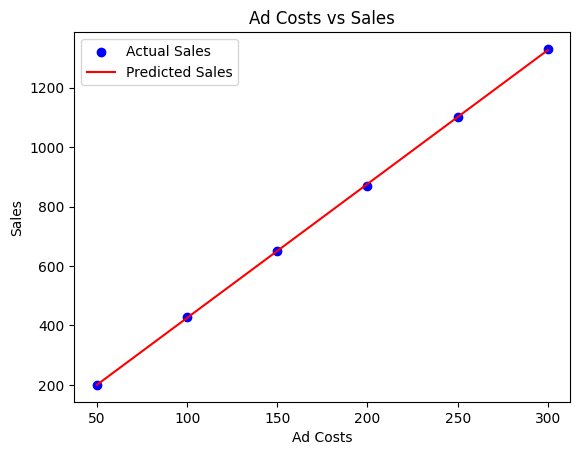
その他の回帰手法
ロジスティック回帰
ロジスティック回帰は、名前に「回帰」とついているものの、実際には分類問題を解くための手法です。特に、二項分類の問題でよく使われます。出力としては、あるカテゴリに属する確率を返します。
数式:
\[ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1X)}} \]
ここで、\( P(Y=1|X) \) は、与えられた特徴 \( X \) を持つデータポイントがカテゴリ1に属する確率を表します。
ロジスティック回帰は、2つのクラスを分類するためのモデルです。データ点と決定境界をプロットすることで、このモデルを視覚的に明示できます。
# データの生成を調整
X, y = make_classification(n_samples=100, n_features=1, n_redundant=0, n_informative=1, n_clusters_per_class=1, random_state=42)
# ロジスティック回帰のフィット
clf = LogisticRegression()
clf.fit(X, y)
# 決定境界の計算
x_values = np.linspace(-3, 3, 100)
y_probs = clf.predict_proba(x_values.reshape(-1, 1))[:, 1]
# グラフのプロット
plt.figure(figsize=(10, 6))
plt.scatter(X, y, c=y, cmap='rainbow', edgecolor='k', alpha=0.7)
plt.plot(x_values, y_probs, color='black')
plt.axhline(0.5, color='red', linestyle='--')
plt.title('Logistic Regression with Decision Boundary')
plt.xlabel('Feature value')
plt.ylabel('Probability')
plt.grid(True)
plt.tight_layout()
plt.show()
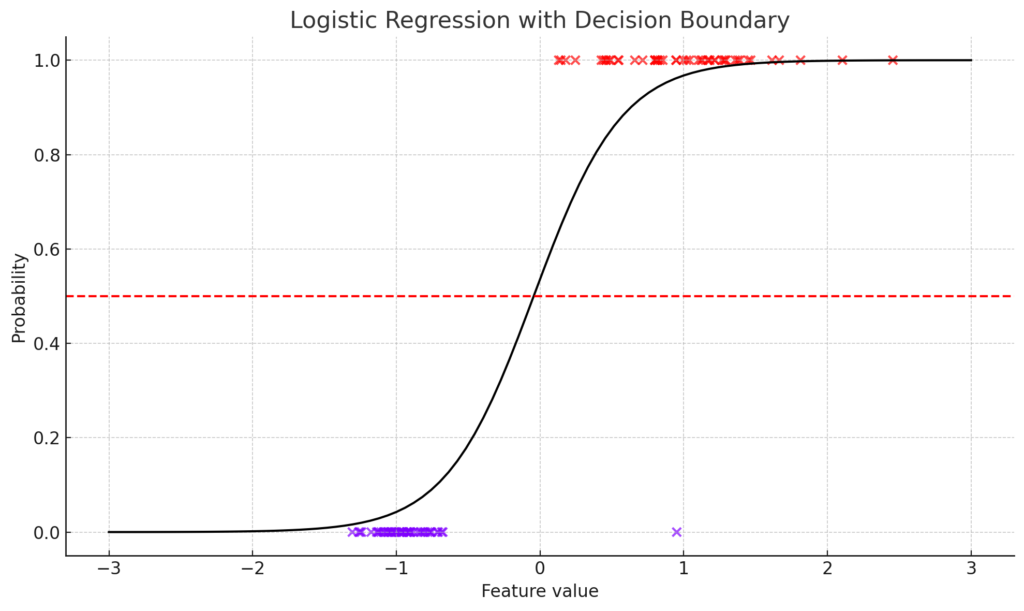
上記のグラフは、ロジスティック回帰の決定境界を示しています。データ点は2つのクラス(色で示されている)に分けられ、黒い線はモデルが予測する確率を示しています。赤い点線は、確率0.5の位置を示しており、これが決定境界となります。
リッジ回帰
リッジ回帰は、線形回帰の一形式で、係数の大きさにペナルティを課す正則化手法を採用しています。これにより、モデルの過学習を防ぎ、予測の安定性を向上させます。リッジ回帰はL2正則化を使用します。
コスト関数:
\[ J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} \theta_i^2 \]
ここで、\( \alpha \) は正則化の強度を制御するパラメータで、大きいほど正則化が強くなります。
リッジ回帰は、L2正則化を使用して特徴の重みを制限する回帰モデルです。特徴の重みの変化をプロットすることで、正則化の強度による影響を視覚的に明示できます。
from sklearn.linear_model import Ridge
from sklearn.datasets import make_regression
# データの生成
X, y = make_regression(n_samples=100, n_features=4, noise=0.1, random_state=42)
# 正則化の強度を変化させる
alphas = np.logspace(-6, 6, 13)
coefs = []
for alpha in alphas:
ridge = Ridge(alpha=alpha)
ridge.fit(X, y)
coefs.append(ridge.coef_)
# グラフのプロット
plt.figure(figsize=(10, 6))
for coef in np.array(coefs).T:
plt.plot(alphas, coef)
plt.xscale('log')
plt.xlabel('Alpha (Regularization Strength)')
plt.ylabel('Feature Weights')
plt.title('Ridge Regression: Feature Weights vs. Regularization Strength')
plt.legend([f'Feature {i+1}' for i in range(X.shape[1])])
plt.grid(True)
plt.tight_layout()
plt.show()
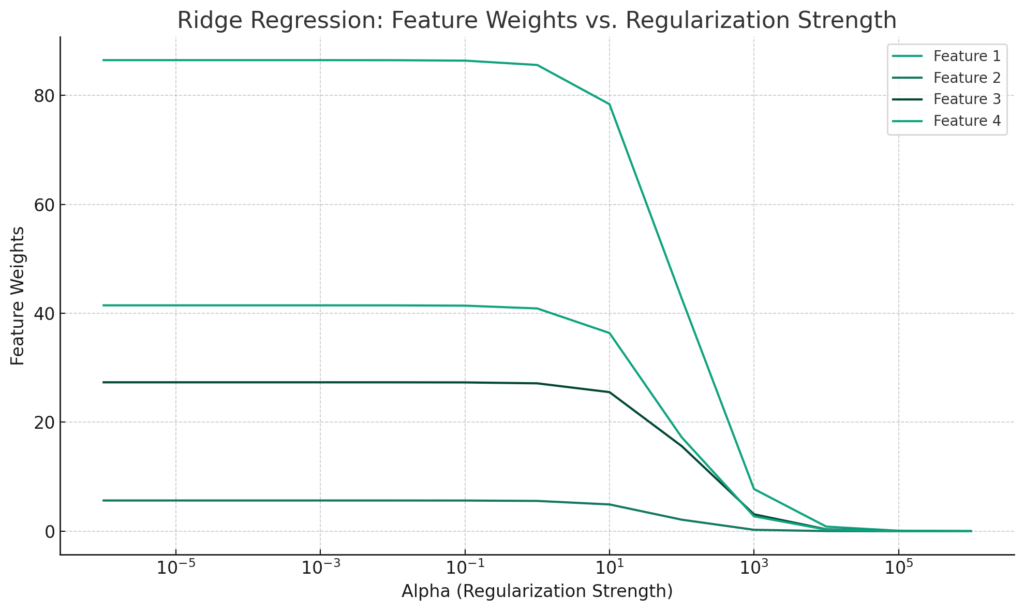
上記のグラフは、リッジ回帰における特徴の重みの変化を、正則化の強度(\(\alpha\))に対してプロットしたものです。正則化の強度が増加するにつれて、各特徴の重みが0に近づくことが視覚的にわかります。
ラッソ回帰
ラッソ回帰も線形回帰の一形式で、リッジ回帰と同様に係数にペナルティを課しますが、L1正則化を使用します。ラッソ回帰の特徴として、不要な特徴の係数を完全に0にすることが挙げられます。これにより、特徴選択の効果も得られます。
コスト関数:
\[ J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} |\theta_i| \]
ここでも、\( \alpha \) は正則化の強度を制御するパラメータです。
下記コードでは、make_regression関数を使用して仮想的な回帰データセットを生成しています。そして、Lassoクラスを使用してラッソ回帰を適用しています。最後に、元のデータとラッソ回帰による予測をグラフにプロットしています。
このコードは、ボストンの住宅価格データセットを使用してラッソ回帰モデルを訓練し、テストデータでの性能を評価します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression
# 仮想データの生成
X, y, true_coefficient = make_regression(n_samples=100, n_features=1, noise=25, coef=True, random_state=0)
# ラッソ回帰のモデルを作成
lasso = Lasso(alpha=1.0)
lasso.fit(X, y)
# データと予測をプロット
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, lasso.predict(X), color='red', label='Lasso Regression')
plt.title('Lasso Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()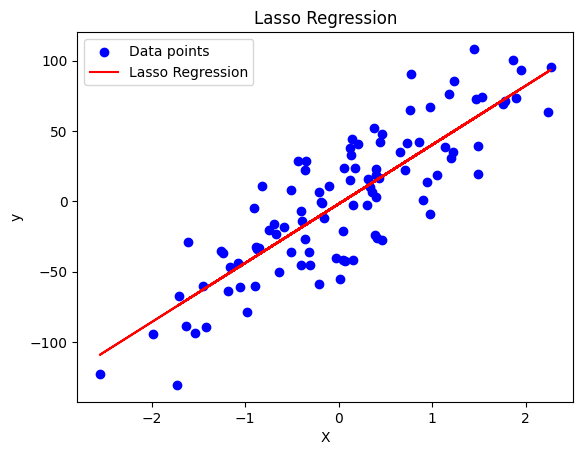
回帰分析の実施手順
データの準備
回帰分析を行う前に、データの適切な準備が必要です。まず、データのクリーニングと前処理を行い、欠損値や外れ値を処理します。次に、データを訓練データとテストデータに分割します。この分割により、モデルの汎化能力を評価できます。
Pythonコードの例(データの分割):
from sklearn.model_selection import train_test_split
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)モデルの選択
適切な回帰モデルを選択することが重要です。データの特性や目的に応じて、単回帰、重回帰、リッジ回帰などのモデルを選びます。
モデルの訓練
訓練データを使用してモデルを訓練します。モデルの訓練は、データに最もよくフィットするようにモデルのパラメータを調整するプロセスです。
Pythonコードの例(線形回帰モデルの訓練):
from sklearn.linear_model import LinearRegression
# モデルの初期化
model = LinearRegression()
# モデルの訓練
model.fit(X_train, y_train)モデルの評価
テストデータを使用して、モデルの性能を評価します。主に、平均二乗誤差(MSE)や決定係数(R^2)などの指標を使用して評価します。
Pythonコードの例(モデルの評価):
from sklearn.metrics import mean_squared_error, r2_score
# 予測
y_pred = model.predict(X_test)
# 平均二乗誤差の計算
mse = mean_squared_error(y_test, y_pred)
# 決定係数の計算
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
print(f"R^2 Score: {r2:.2f}")このステップで、回帰分析の基本的な手順を理解できます。実際のデータに対してこれらの手順を適用する際には、データの特性や目的に応じて適切なモデルや評価指標を選択することが重要です。
回帰分析の注意点
過学習とは
過学習(Overfitting)は、モデルが訓練データに過度に適合してしまい、新しい未知のデータに対しての予測性能が低下してしまう現象を指します。一般的に、モデルの複雑さが増すと過学習のリスクが高まります。過学習を防ぐためには、正則化やクロスバリデーションなどの手法が有効です。
グラフの例:
- X軸にエポック数、Y軸に訓練データと検証データの誤差をプロットして、過学習の兆候を視覚的に捉える。
以下は、このグラフを作成するPythonコードの例です。過学習の兆候としては、訓練データの誤差は徐々に減少していくのに対して、検証データの誤差がある点から増加し始める場合が考えられます。今回は、そのようなデータを仮定してグラフを作成します。
import matplotlib.pyplot as plt
import numpy as np
# 仮のエポック数と誤差データ
epochs = np.arange(1, 21)
train_loss = 1 / (epochs + 1) + np.random.normal(0, 0.05, len(epochs))
validation_loss = 1 / (epochs + 1) + np.random.normal(0, 0.05, len(epochs)) + epochs * 0.02
plt.figure(figsize=(10, 6))
plt.plot(epochs, train_loss, label='Training Loss', marker='o')
plt.plot(epochs, validation_loss, label='Validation Loss', marker='x')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training and Validation Loss Over Epochs')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()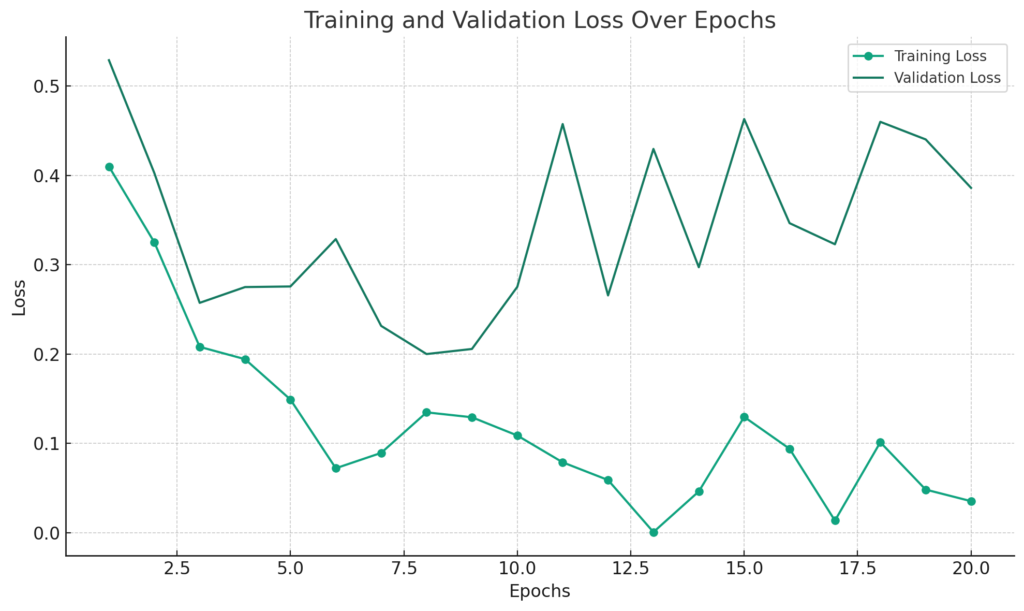
上記のグラフでは、エポック数が増加するにつれて訓練データの誤差は減少しますが、検証データの誤差はある点から増加しています。これは過学習の兆候として捉えることができます。
多重共線性の問題
多重共線性は、説明変数間に強い相関が存在する場合に発生する問題です。これにより、回帰係数の推定が不安定になったり、誤った結論を導く可能性があります。多重共線性を確認するためには、VIF(Variance Inflation Factor)を計算すると有効です。VIFが大きい場合は、多重共線性の可能性が高いと考えられます。
Pythonコードの例(VIFの計算):
from statsmodels.stats.outliers_influence import variance_inflation_factor
# VIFの計算
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
vif["features"] = X.columns
print(vif)外れ値の影響
外れ値は、他のデータと大きく異なる値を持つデータポイントを指します。外れ値の存在は、回帰分析の結果に大きな影響を及ぼす可能性があります。外れ値の影響を減少させるためには、データの前処理段階で外れ値を検出し、適切に処理することが重要です。
グラフの例:
- 残差プロットを使用して、外れ値を視覚的に確認する。
残差プロットを使用して外れ値を視覚的に確認するグラフを作成します。このグラフでは、予測値と実際の値の差(残差)をY軸に、予測値をX軸に取ります。外れ値は、他のデータ点から離れてプロットされるため、視覚的に識別できます。
以下は、このグラフを作成するPythonコードの例です。
# 仮の予測値と実際の値
predicted_values = np.linspace(10, 50, 100)
actual_values = predicted_values + np.random.normal(0, 5, len(predicted_values))
# 外れ値を追加
predicted_values = np.append(predicted_values, [20, 35])
actual_values = np.append(actual_values, [0, 80])
# 残差の計算
residuals = actual_values - predicted_values
plt.figure(figsize=(10, 6))
plt.scatter(predicted_values, residuals, alpha=0.6)
plt.axhline(0, color='red', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.grid(True)
plt.tight_layout()
plt.show()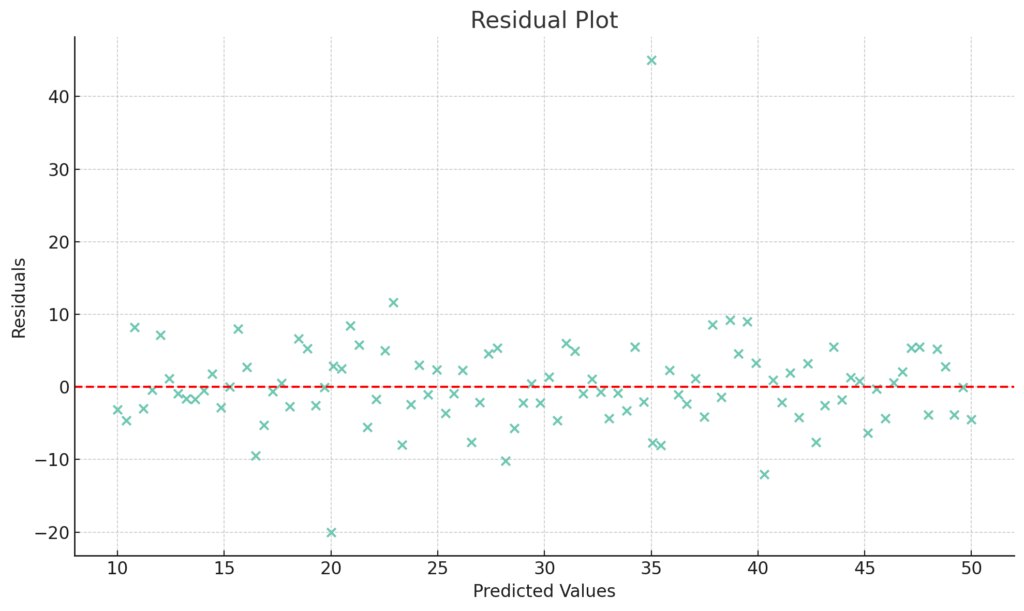
上記の残差プロットでは、大部分のデータ点が赤い点線(残差が0の位置)の周りに集まっていますが、2つの明らかな外れ値(予測値が約20の位置と約35の位置)が確認できます。これにより、モデルが一部のデータ点を適切に予測できていないことが視覚的にわかります。
まとめ
回帰分析は、変数間の関係を明らかにする強力な手法ですが、正確な結果を得るためには注意が必要です。過学習、多重共線性、外れ値の影響は、回帰分析の結果に大きな影響を及ぼす可能性があります。これらの問題を理解し、適切に対処することで、信頼性の高い回帰分析を実施できます。

▼AIを使った副業・起業アイデアを紹介♪
