データサイエンティストの必須知識、「推測統計学と記述統計学、確率 | 統計学の基礎」について解説します。
推測統計学、記述統計学、確率の基礎
不確実性のあるデータと確率
毎日の生活の中で、私たちは不確実性に直面しています。例えば、明日の天気や電車が定刻に来るかどうか、株価の動きなどの事象の結果は確定的には知ることができません。
このような不確実性のあるデータや事象を数学的に扱うために、確率という概念が導入されます。
確率の基本
確率は、事象が発生する可能性を0から1の間の数値で表すものです。0は事象が絶対に発生しないことを、1は事象が絶対に発生することを意味します。
例: コインを投げたとき、表が出る確率は0.5、裏が出る確率も0.5です。
\[ P(\text{表}) = 0.5 \]
\[ P(\text{裏}) = 0.5 \]
ここで、\( P(\text{事象}) \) は「事象が発生する確率」という意味です。
不確実性とデータ
データ分析では、収集したデータには必ずと言っていいほどノイズや不確実性が含まれます。この不確実性を理解し、適切にモデル化することで、より正確な予測や分析を実施できます。
Pythonを使って、サイコロを100回振ったときの結果をシミュレートしてみましょう。
import numpy as np
import matplotlib.pyplot as plt
# サイコロを100回振る
rolls = np.random.choice([1,2,3,4,5,6], 100)
# 結果をヒストグラムで表示
plt.hist(rolls, bins=[0.5,1.5,2.5,3.5,4.5,5.5,6.5], rwidth=0.8)
plt.title("Results of rolling a dice 100 times")
plt.xlabel("Dice Value")
plt.ylabel("Frequency")
plt.show()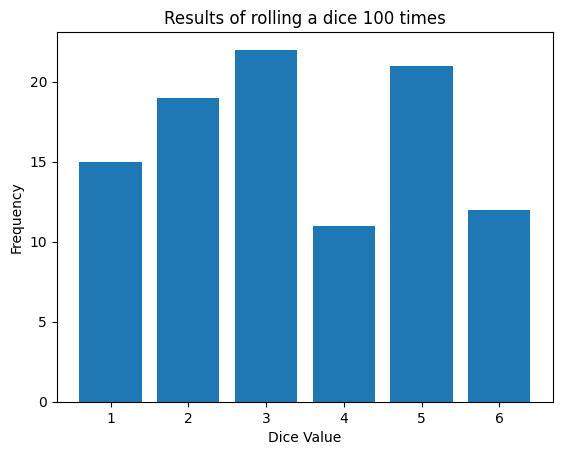
このグラフから、各目の出る回数にはばらつきがあることがわかります。このばらつきや不確実性をうまく扱うのが、確率や統計学の役割です。
母集団と標本
母集団とは?
母集団とは、調査や研究の対象となる全体のことを指します。例えば、ある会社の全従業員、ある国の全住民などが考えられます。
標本とは?
一方、標本は母集団の一部をランダムに選んだものです。全てのデータを調査するのは時間やコストがかかるため、一部のデータだけを取り出して分析することが多いです。
Pythonでのシミュレーション
以下は、10000人の人々が所持しているお金の平均を計算するシミュレーションです。全体を母集団とし、その中から1000人をランダムに選ぶ標本を取ります。
import numpy as np
# 10000人の所持金を生成
population = np.random.randint(0, 50001, 10000)
# 1000人をランダムに選ぶ
sample = np.random.choice(population, 1000)
print(f"Population Mean: {np.mean(population)}")
print(f"Sample Mean: {np.mean(sample)}")
Population Mean: 24943.9609
Sample Mean: 24607.26このシミュレーションから、標本の平均が母集団の平均に近いことがわかります。しかし、完全に同じにはなりません。
記述統計学と推測統計学
記述統計学
記述統計学は、データの特徴を要約し、理解しやすくするための手法です。平均、中央値、標準偏差などの基本的な統計量を使用して、データの分布や形状を説明します。
推測統計学
推測統計学は、標本を使って母集団の特性を推測する手法です。例えば、ある標本のデータから、母集団の平均や分散を推測できます。
例
あるクラスの学生10人のテストの点数を使って、学年全体の平均点を推測する場合、この10人の点数は標本となります。この標本の平均や標準偏差を計算し、それを基に学年全体の平均点を推測するのが推測統計学の一例です。
確率変数
確率変数は、ランダムな事象の結果に数値を割り当てる変数です。例えば、コインを投げる事象で「表」が出た場合に1、「裏」が出た場合に0を割り当てる場合、この変数は確率変数となります。
例: サイコロの投げ
サイコロを投げたときの目を表す変数Xを考えます。このXは確率変数であり、1から6までの整数の値を取ることができます。
確率分布
確率分布は、確率変数が取りうる各値と、その値を取る確率との間の関係を示します。
例: サイコロの投げ
上記のサイコロの例では、各目が出る確率は1/6です。したがって、確率分布は以下のようになります。
\[ P(X = 1) = \frac{1}{6} \]
\[ P(X = 2) = \frac{1}{6} \]
\[ \vdots \]
\[ P(X = 6) = \frac{1}{6} \]
分布関数
分布関数(累積分布関数)は、確率変数がある値以下となる確率を示す関数です。確率変数Xに対する分布関数を\( F(x) \)とすると、\( F(x) \)は「確率変数Xがx以下となる確率」と解釈できます。
例: サイコロの投げ
サイコロの例での分布関数は以下のように定義されます。
\[ F(1) = P(X \leq 1) = \frac{1}{6} \]
\[ F(2) = P(X \leq 2) = \frac{2}{6} \]
\[ \vdots \]
\[ F(6) = P(X \leq 6) = 1 \]
Pythonでの可視化
import numpy as np
import matplotlib.pyplot as plt
# サイコロの確率分布
values = np.arange(1, 7)
probabilities = [1/6] * 6
# 累積分布関数の計算
cum_probs = np.cumsum(probabilities)
plt.step(values, cum_probs, where='post')
plt.xlabel("Value")
plt.ylabel("Probability")
plt.title("Cumulative Distribution Function (CDF) of a Dice Roll")
plt.xticks(values)
plt.yticks(np.linspace(0, 1, 7))
plt.grid(True)
plt.show()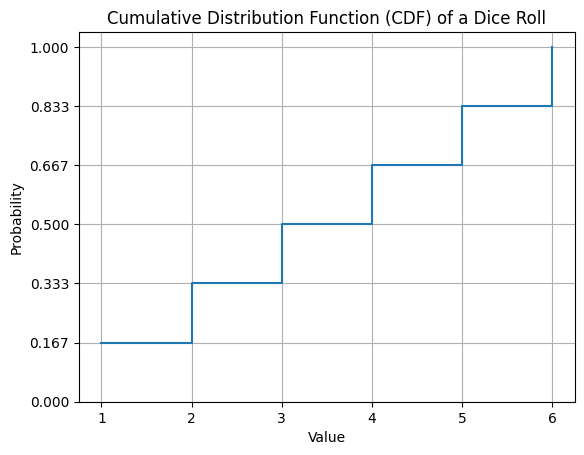
このグラフは、サイコロを投げたときの結果の累積分布関数を示しています。

▼AIを使った副業・起業アイデアを紹介♪
