次元削減と主成分分析 | 機械学習の基礎 | AIエンジニアに転職して年収アップガイド

次元削減と主成分分析の基礎
まとめ

次元削減と主成分分析の基礎

次元削減の基本的な概念

次元の呪い

次元の呪いとは、データの次元が増加するとそのデータを扱う際の難易度や計算量が指数関数的に増加する現象を指します。高次元空間では、データポイント間の距離がほぼ等しくなり、多くの機械学習アルゴリズムがうまく機能しなくなります。

次元削減のメリット

計算効率の向上: データの次元が減少することで、計算コストやストレージの要件が減少します。
可視化: 2または3の次元にデータを削減することで、データの可視化が可能になり、データの構造やパターンを直感的に理解するのに役立ちます。
過学習の軽減: 不要な特徴を取り除くことで、モデルがノイズに過度に適応するのを防ぎます。
ノイズ除去: 主な特徴を保持しながらノイズを取り除くことができます。

次元削減の応用例

画像処理: 高次元の画像データを効果的に圧縮や特徴抽出するために使用されます。
遺伝子データの解析: 高次元の遺伝子データから主なパターンや情報を抽出するために使用されます。
推薦システム: 大量の特徴を持つ商品やユーザーのプロファイルを効果的に圧縮して、推薦の質を向上させるために使用されます。

これらの概念を理解することで、次元削減の重要性とその応用例についての洞察を深めることができます。

主成分分析(PCA)の概要

PCAの定義

主成分分析（PCA: Principal Component Analysis）は、多変量データの情報を圧縮しながら、データの分散を最大にする新しい軸（主成分）を見つけ出す統計的手法です。これにより、データの次元を削減できます。具体的には、データの共分散行列の固有ベクトルと固有値を計算することで、新しい特徴空間を形成します。

PCAの動機と目的

データの可視化: 高次元のデータを2Dまたは3D空間に圧縮することで、データの構造や関係性を直感的に理解するのに役立ちます。
ノイズの除去: 主な特徴を保持しながら、データのノイズや冗長な情報を取り除くことができます。
計算効率の向上: 次元が削減されたデータは、計算コストやストレージの要件が少なくなるため、機械学習アルゴリズムの学習や予測が高速になります。
特徴選択: 多数の関連する特徴から、最も情報を持つ特徴を抽出できます。

数式での説明:
データの共分散行列\( C \)の固有ベクトルと固有値を求めることで、主成分を決定します。共分散行列の固有ベクトルが新しい特徴空間の軸となり、対応する固有値はその軸の分散を示します。

\[ C \mathbf{v}_i = \lambda_i \mathbf{v}_i \]

ここで、\( \mathbf{v}_i \)はi番目の固有ベクトル、\( \lambda_i \)はi番目の固有値を示します。

PCAの目的は、上記の固有ベクトルを使用して、データを新しい低次元の特徴空間に射影することにあります。

この概念を理解することで、PCAの動機とその実用性についての洞察を深めることができます。

PCAのアルゴリズムの流れ

データの中心化

PCAを行う前の最初のステップは、データの中心化です。これは、各特徴の平均が0になるようにデータを変換することを意味します。

\[
X_{\text{centered}} = X – \mu
\]

ここで、\( \mu \)はデータセットの平均ベクトルです。

共分散行列の計算

次に、中心化されたデータの共分散行列を計算します。共分散行列は、データの特徴間の関連性を捉えるためのものです。

\[
C = \frac{1}{N-1} X_{\text{centered}}^T X_{\text{centered}}
\]

固有値と固有ベクトルの計算

共分散行列の固有値と固有ベクトルを計算します。これらの固有ベクトルは、新しい特徴空間の基底として機能し、対応する固有値はその方向の分散を示します。

主成分の選択

固有値が大きい順に固有ベクトルをソートし、上位k個の固有ベクトルを選択します。このkは、新しい特徴空間の次元数を示します。

新しい特徴空間への射影

選択された固有ベクトルを使用して、データを新しい低次元の特徴空間に射影します。

\[
X_{\text{pca}} = X_{\text{centered}} \times W
\]

ここで、\( W \)は選択されたk個の固有ベクトルから形成される行列です。

以下は、Pythonのscikit-learnライブラリを使用したPCAの実装例です。

from sklearn.decomposition import PCA# データのロードと中心化# X is your datasetX_centered = X - X.mean(axis=0)# PCAの適用pca = PCA(n_components=2)  # 2次元に削減X_pca = pca.fit_transform(X_centered)# X_pca is now the transformed data in the new feature space.

このアルゴリズムの流れを理解することで、PCAがどのようにデータを低次元の特徴空間に変換するか、その背後にある数学的な理由を理解できます。

PCAの実践

PythonでのPCAの実装例

主成分分析をPythonで実装するには、scikit-learnライブラリのPCAクラスを使用するのが一般的です。以下は、このクラスを使用してPCAを実装する基本的なステップです。

必要なライブラリをインポートします。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

データセットをロードします。ここでは、例としてIrisデータセットを使用します。

data = load_iris()
X = data.data
y = data.target

PCAを実行します。この例では、2次元にデータを削減します。

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

PCAの結果の可視化

PCAの結果を可視化することで、データの構造やクラスタリングを直感的に理解できます。以下は、PCAの結果を2Dプロットとして可視化する方法です。

# プロットの準備
colors = ['r', 'g', 'b']
targets = [0, 1, 2]
labels = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']

# 2Dプロットの作成
for target, color, label in zip(targets, colors, labels):
    plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], color=color, label=label)

plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('2D PCA of Iris Dataset')
plt.legend()
plt.grid(True)
plt.show()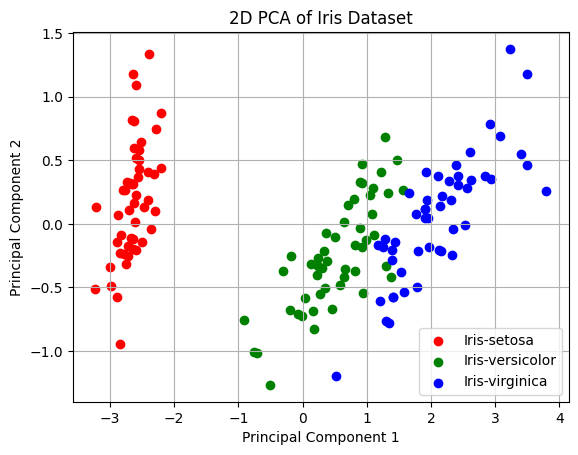

このグラフは、Irisデータセットの3つのクラス（Iris-setosa、Iris-versicolor、Iris-virginica）が、PCAによって2次元空間にどのようにマッピングされるかを示しています。主成分分析によって、これらのクラスが明確に分離されることが分かります。

PCAの利点と制約

利点

データの可視化: 高次元データを2次元や3次元に削減して可視化できる。
計算効率: 一部の機械学習アルゴリズムの計算時間やメモリ使用量を削減できる。
ノイズの除去: データの主な変動をキャッチすることで、ノイズを減少させる。
特徴選択: 最も情報量の多い特徴を選択し、不要な特徴を除去できる。

制約

情報の損失: 元のデータの一部の情報を失う可能性がある。
解釈性の低下: 主成分は元の特徴とは異なるため、結果の解釈が難しくなる場合がある。
線形の制約: PCAは線形な手法であるため、非線形のデータ構造を捉えることができない。

その他の次元削減の手法

t-SNE

t-SNE（t-distributed Stochastic Neighbor Embedding）は、高次元データの可視化に特に適した次元削減手法です。t-SNEは、高次元空間のデータポイント間の距離と低次元空間のデータポイント間の距離を最もよく一致させるように設計されています。

LDA

LDA（Linear Discriminant Analysis）は、クラスの分離を最大化する方向にデータを射影する次元削減手法です。LDAは教師あり学習の手法であり、PCAとは異なり、クラスラベルを使用します。

オートエンコーダ

オートエンコーダは、ニューラルネットワークを用いた次元削減手法です。入力データを低次元の特徴にエンコードし、その特徴から元のデータを再構築（デコード）することを学習します。オートエンコーダは、非線形なデータ構造を捉えることができ、深層学習の領域で広く使用されています。

これらの手法は、データの構造や目的に応じて選択されるべきです。PCAは線形な手法としての利点と制約がありますが、その他の手法はそれぞれ異なる特性や利用シーンがあります。次元削減の方法を選択する際には、データの特性や目的を考慮することが重要です。

まとめ

次元削減は、高次元データを低次元空間に変換する技術で、データの可視化、計算効率の向上、ノイズの除去など、さまざまな目的で使用されています。特に「次元の呪い」に対処するための重要な手段として注目されています。

主成分分析（PCA）は、次元削減の中でも特に人気の手法であり、データの分散を最大化する方向に変換することで、情報の損失を最小限に抑えながら次元を削減します。PCAのアルゴリズムは、データの中心化、共分散行列の計算、固有値と固有ベクトルの計算、主成分の選択、新しい特徴空間への射影というステップで構成されています。

PCAは、その線形性と計算の効率性から多くの分野で広く利用されていますが、線形の制約があるため、非線形のデータ構造を持つデータには適していない場合があります。

そのため、非線形のデータ構造を考慮した次元削減の手法、例えばt-SNEやオートエンコーダなども紹介しました。これらの手法は、PCAとは異なるアプローチで次元削減し、特定のデータや目的に合わせて選択します。

次元削減やPCAはデータ解析の初歩としてとても重要な技術です。しかし、どの手法を選択するか、その手法の背後にある仮定や制約を理解することが、適切なデータ解析の鍵となります。