ベイジアンモデルの基礎
ベイジアンモデルは、確率的な事象やデータに関する不確実性を扱うための統計的手法の一つです。この手法はベイズの定理を基盤としており、事前の知識(事前確率)と新しいデータ(尤度)を組み合わせて、事後の知識(事後確率)を更新するという考え方を採用しています。
ベイジアンモデルのメリット
- 事前知識の組み込み: ベイジアンモデルは事前知識や信念を組み込むことができます。これにより、過去の経験や専門家の意見をモデルに反映させます。
- 不確実性の明確な取り扱い: ベイジアンモデルは確率を使って不確実性を明確に取り扱うことができます。これにより、予測の信頼性やリスクを評価する際に有用です。
- データが少ない場合でも有効: データが少ない場合やデータが不完全な場合でも、事前知識を利用して予測できます。
線形回帰を例として、ベイジアン線形回帰と通常の最小二乗法線形回帰を比較します。データはシンプルな線形関係を持つデータセットを生成し、ノイズを加えて使用します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import pymc3 as pm
# データセットの生成
np.random.seed(42)
X = np.linspace(0, 10, 100)[:, None]
y = 2 * X.flatten() + 1 + np.random.randn(100) * 2
# 最小二乗法線形回帰
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_pred_lin_reg = lin_reg.predict(X)
# ベイジアン線形回帰
with pm.Model() as model:
alpha = pm.Normal('alpha', mu=0, sd=10)
beta = pm.Normal('beta', mu=0, sd=10)
sigma = pm.HalfNormal('sigma', sd=1)
y_est = alpha + beta * X.flatten()
likelihood = pm.Normal('y', mu=y_est, sd=sigma, observed=y)
trace = pm.sample(2000, tune=1000)
alpha_mcmc = np.mean(trace['alpha'])
beta_mcmc = np.mean(trace['beta'])
y_pred_bayesian = alpha_mcmc + beta_mcmc * X.flatten()
# グラフの表示
plt.figure(figsize=(10, 6))
plt.scatter(X, y, s=30, label='Data')
plt.plot(X, y_pred_lin_reg, 'r', label='OLS Linear Regression')
plt.plot(X, y_pred_bayesian, 'g', label='Bayesian Linear Regression')
plt.title('Comparison between OLS and Bayesian Linear Regression')
plt.legend()
plt.show()このコードでは、pymc3というライブラリを使用してベイジアン線形回帰を行っています。結果のグラフでは、赤色が最小二乗法線形回帰の予測、緑色がベイジアン線形回帰の予測を示しています。
ベイジアンモデルの種類
ベイジアンモデルにはさまざまな種類がありますが、以下は主なものをいくつか紹介します。
- ベイジアンネットワーク: グラフィカルな表現を持つ確率モデルで、変数間の因果関係や依存関係を明示的に表現します。
例: 病気の診断、推薦システムなど。 - ベイジアン回帰: 線形回帰やロジスティック回帰のベイジアン版で、回帰係数の不確実性を確率的に扱います。
- トピックモデル: ドキュメントのトピックを確率的に推定するモデル。
例: Latent Dirichlet Allocation (LDA) - 階層的ベイズモデル: 複数の階層を持つベイジアンモデルで、グループ間の情報を共有しながら個々のグループの特性も考慮します。
例: 複数の店舗や国に関するデータの解析。
ベイズの定理
ベイズの定理とは?
ベイズの定理は確率論における基本的な定理の一つで、事前の知識や信念と新しい観測データを組み合わせて、ある仮説の確率を更新する方法を提供します。数式で表すと以下のようになります。
\[
P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}
\]
ここで、
- \( P(A|B) \) は事後確率と呼ばれ、データBが与えられたときの仮説Aの確率を示します。
- \( P(B|A) \) は尤度と呼ばれ、仮説Aが真であるときのデータBの確率を示します。
- \( P(A) \) は事前確率と呼ばれ、新しいデータBが観測される前の仮説Aの確率を示します。
- \( P(B) \) は証拠または全体確率と呼ばれ、任意の仮説に関わらずデータBが観測される確率を示します。
ベイズの定理の応用
ベイズの定理は多岐にわたる分野での応用があります。
- 医療: 病気の診断において、特定の症状を持つ患者がある病気を持っている確率を計算する。
- 機械学習: クラス分類や回帰分析などの問題において、データをもとにモデルのパラメータを更新する。
- フィルタリング: スパムメールの検出や推薦システムなどで、あるアイテムがユーザーの興味を引くものである確率を計算する。
ベイジアン推論
ベイジアン推論とは?
ベイジアン推論は、ベイズの定理を基盤として不確実性を持つパラメータやモデルの構造に関する信念を、データを通じて更新するプロセスです。ベイジアン推論の目的は、事後確率分布を計算することであり、この分布は新しいデータが与えられたときのパラメータやモデルの構造に関する不確実性を反映します。
ベイジアン推論の種類
- 解析的推論: 事後確率分布を直接計算する方法。簡単なモデルや小さなデータセットに適していますが、複雑なモデルや大規模なデータセットでは計算が難しくなることがあります。
- 数値的推論: 事後確率分布を近似するためのサンプリング技術や最適化技術を使用する方法。MCMC (Markov Chain Monte Carlo) や変分ベイズ法などがあります。
ベイジアン推論のアルゴリズム
- MCMC (Markov Chain Monte Carlo): 事後確率分布からのサンプルを生成するためのアルゴリズム。Metropolis-HastingsアルゴリズムやGibbsサンプリングなどの手法があります。
- 変分ベイズ法: 事後確率分布を簡単な分布で近似するアルゴリズム。大規模なデータセットや複雑なモデルに対して高速に動作することが多い。
ベイジアンモデルの応用
自然言語処理
ベイジアンモデルは自然言語処理(NLP)の分野で幅広く利用されています。特にトピックモデリングや文書分類、センチメント分析などのタスクでの応用が見られます。ベイジアンアプローチは、テキストデータの不確実性や曖昧さを効果的に扱うことができます。
トピックの分布をグラフで表示
import gensim
from gensim import corpora
from nltk.corpus import stopwords
import matplotlib.pyplot as plt
# データセットの準備
documents = [
"Sugar is bad for health.",
"My cat is sweet.",
"Dogs and cats are enemies.",
"Health professionals suggest reducing sugar in diet.",
"Cats are lovely animals."
]
# 前処理
stop_words = set(stopwords.words('english'))
texts = [[word for word in document.lower().split() if word not in stop_words] for document in documents]
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# LDAの適用
lda_model = gensim.models.LdaModel(corpus, num_topics=2, id2word=dictionary, passes=15)
# トピックの表示
topics = lda_model.print_topics(num_words=5)
for topic in topics:
print(topic)
# トピックの分布をグラフで表示
for index, score in sorted(lda_model[corpus[2]], key=lambda tup: -1*tup[1]):
plt.bar(["Topic "+str(index)], [score])
plt.title("Topic distribution for the sentence: 'Dogs and cats are enemies.'")
plt.show()このコードは、gensimとnltkというライブラリを使用しています。トピックモデリングの結果として、各トピックの上位の単語が表示されます。また、特定の文(ここでは”犬と猫は敵だ。”)におけるトピックの分布を示すグラフも表示されます。
機械学習
ベイジアンモデルは機械学習の分野でも重要な役割を果たしています。ベイジアン回帰やベイジアンネットワークなどのモデルは、データの不確実性を考慮しながら予測できます。また、ベイジアン最適化は、ハイパーパラメータの調整や機械学習モデルの選択に利用されます。
ベイジアンリッジ回帰
ベイジアンモデルの機械学習アプローチの一例として、ベイジアンリッジ回帰を考えます。この手法は、リッジ回帰にベイズ的な解釈を適用したもので、回帰係数に事前分布を設定します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
# データセットの生成
np.random.seed(42)
X = np.linspace(0, 10, 100)[:, None]
y = 2 * X.flatten() + 1 + np.random.randn(100) * 2
# ベイジアンリッジ回帰の適用
bayesian_ridge = BayesianRidge()
bayesian_ridge.fit(X, y)
y_pred = bayesian_ridge.predict(X)
# 予測結果のグラフ表示
plt.figure(figsize=(10, 6))
plt.scatter(X, y, s=30, label='Data')
plt.plot(X, y_pred, 'r', label='Bayesian Ridge Regression')
plt.title('Bayesian Ridge Regression')
plt.legend()
plt.show()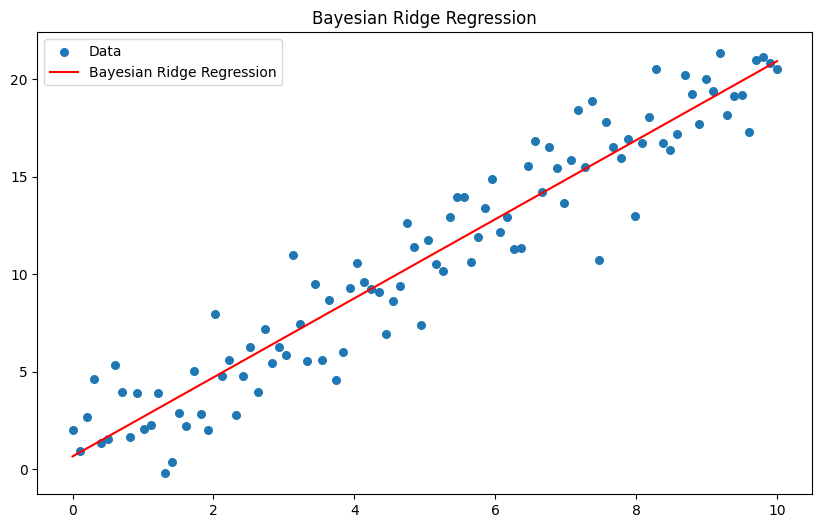
このコードでは、sklearnのBayesianRidgeを使用してベイジアンリッジ回帰を行います。結果のグラフでは、赤色がベイジアンリッジ回帰の予測を示しています。データポイントと予測線を比較することで、モデルの学習結果を視覚的に評価できます。
統計学
ベイジアンモデルは、統計学の伝統的な手法とは異なる視点を提供します。ベイジアン統計学は、事前知識とデータを組み合わせて、モデルのパラメータや構造に関する不確実性を評価します。これにより、リスクや信頼区間の評価がより直感的に行えます。
コインの不公平さ(表が出る確率)を推定
ベイジアン統計学の具体的な応用例として、コイン投げの実験を考えます。ベイジアンアプローチを用いて、コインの不公平さ(表が出る確率)を推定します。
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt
# データの生成
np.random.seed(42)
n_trials = 100
theta_real = 0.6 # 実際のコインの不公平さ
data = np.random.binomial(n=1, p=theta_real, size=n_trials)
# ベイジアン統計モデルの構築
with pm.Model() as coin_model:
theta = pm.Beta('theta', alpha=1, beta=1)
y = pm.Bernoulli('y', p=theta, observed=data)
trace = pm.sample(1000, random_seed=42)
# 事後分布のグラフ表示
plt.figure(figsize=(10, 6))
plt.hist(trace['theta'], bins=30, density=True, alpha=0.75)
plt.axvline(theta_real, color='red', label=f"True value ({theta_real})")
plt.xlabel(r"$\theta$")
plt.ylabel("Density")
plt.title("Posterior distribution of parameter theta")
plt.legend()
plt.show()このコードでは、pymc3ライブラリを使用してベイジアン統計モデリングを行います。事後分布のグラフでは、真のパラメータ値(赤線)と比較して、推定されたパラメータの分布を示しています。
まとめ
ベイジアンモデルは、不確実性を持つデータや事象を扱うための強力なツールです。ベイズの定理を基盤として、事前の知識や信念を新しいデータと組み合わせて信念を更新する手法を採用しています。自然言語処理、機械学習、統計学など、多岐にわたる分野での応用が見られます。ベイジアンモデルは、データ駆動の時代において、複雑な問題を解決するための鍵となるでしょう。

▼AIを使った副業・起業アイデアを紹介♪
