データサイエンティストの必須知識、「データの特徴を視覚的に明らかにする | 統計学の基礎」について解説します。
情報の特性を視覚的に示す主な方法
度数分布表
定義と目的
度数分布表は、データセット内のデータが取る異なる値の範囲ごとに、その値の出現回数をまとめた表です。これにより、データの分布を視覚的に理解しやすくなります。特に、大量のデータを扱う際に、データの傾向や分布を一目で把握するのに役立ちます。
作成方法
- データの最小値と最大値を決定します。
- データをいくつかのクラス(範囲)に分けます。このとき、各クラスの幅を一定にすることが一般的です。
- 各クラスに含まれるデータの数(度数)を数え上げます。
- 各クラスの下限と上限、度数を表に記入します。
実例と解釈
例えば、あるクラスのテストの点数が以下のように与えられたとします。
\[ \text{点数: } 56, 78, 90, 85, 72, 94, 88, 79, 67, 92 \]
このデータを度数分布表で表示すると以下のようになります。
import pandas as pd
import numpy as np
# データ
scores = [56, 78, 90, 85, 72, 94, 88, 79, 67, 92]
# ビンの範囲を指定
bins = [50, 60, 70, 80, 90, 100]
# 度数分布表を作成
hist, edges = np.histogram(scores, bins=bins)
df = pd.DataFrame({'範囲': [f"{edges[i]}-{edges[i+1]}" for i in range(len(edges)-1)], '度数': hist})
print(df) 範囲 度数
0 50-60 1
1 60-70 1
2 70-80 3
3 80-90 2
4 90-100 3この度数分布表から、ほとんどの生徒が70点以上のスコアを獲得したことが分かります。また、最も多いスコアの範囲は80-90点であることも分かります。
このように、度数分布表はデータの全体的な傾向や分布を簡単に確認できる便利なツールです。
ヒストグラム
ヒストグラムは、データの分布を視覚的に理解するためのグラフィカルな手法です。データの頻度や度数を縦軸に、データの範囲やビンを横軸に表示します。
定義と目的
ヒストグラムは、連続データを一定の範囲(ビンやクラスと呼ばれる)に分け、各範囲に含まれるデータの数(度数)を棒グラフで示したものです。ヒストグラムの目的は以下のとおりです。
- データの分布を視覚的に理解する。
- データの中央値やモード(最頻値)を特定する。
- 異常値や外れ値の存在を確認する。
- データの偏りや歪みを評価する。
作成方法
Pythonでヒストグラムを作成するには、matplotlibやseabornといったライブラリを使用します。以下はmatplotlibを使用した基本的なヒストグラムの作成方法です。
import matplotlib.pyplot as plt
# Sample data
data = [51, 53, 54, 55, 60, 62, 65, 65, 68, 70, 72, 75, 76, 78, 80, 82, 85, 88, 90, 93]
# Create histogram
plt.hist(data, bins=10, edgecolor='black') # bins represents the number of bins
plt.title('Histogram Sample')
plt.xlabel('Data Range')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()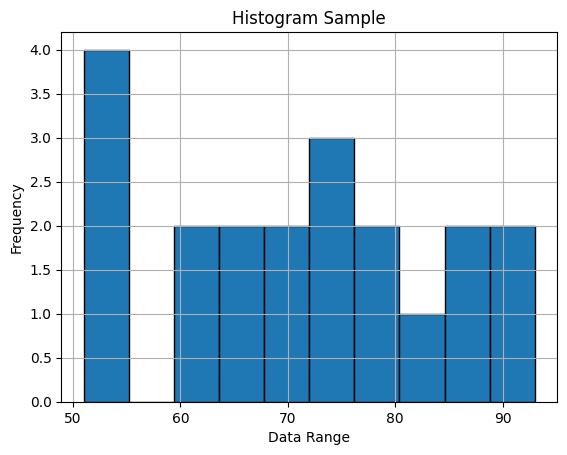
このコードを実行すると、データの分布を示すヒストグラムが表示されます。ビンの数や範囲を調整することで、データの特性に合わせたヒストグラムを作成できます。
相対度数・累積度数・累積相対度数
定義と目的
相対度数、累積度数、および累積相対度数は、データセットの特徴を理解するための基本的な統計的手法です。
- 相対度数: 各クラスの度数を全データの数で割ったもの。データの特定の部分が全体に占める割合を示します。
- 累積度数: 各クラスまでの度数の合計。データがどれだけ蓄積されているかを示します。
- 累積相対度数: 累積度数を全データの数で割ったもの。データの蓄積の割合を示します。
これらの統計は、データの分布やトレンドを視覚的に理解するのに役立ちます。
計算方法
以下は、それぞれの計算方法を示す数式です。
\[
\text{相対度数} = \frac{\text{度数}}{\text{全データの数}}
\]
\[
\text{累積度数} = \text{前のクラスまでの累積度数} + \text{現在のクラスの度数}
\]
\[
\text{累積相対度数} = \frac{\text{累積度数}}{\text{全データの数}}
\]
実例と解釈
例として、ある試験の得点のデータセットを考えます。10点刻みの得点範囲に基づいてデータをグルーピングします。
import pandas as pd
# サンプルデータ
scores = [56, 78, 90, 85, 72, 94, 88, 79, 67, 92]
# ビンの範囲を指定
bins = [50, 60, 70, 80, 90, 100]
# 度数を計算
hist, _ = np.histogram(scores, bins=bins)
# 相対度数、累積度数、累積相対度数を計算
relative_frequency = hist / len(scores)
cumulative_frequency = np.cumsum(hist)
cumulative_relative_frequency = cumulative_frequency / len(scores)
# 結果をデータフレームにまとめる
df = pd.DataFrame({
'Score Range': [f"{bins[i]}-{bins[i+1]}" for i in range(len(bins)-1)],
'Frequency': hist,
'Relative Frequency': relative_frequency,
'Cumulative Frequency': cumulative_frequency,
'Cumulative Relative Frequency': cumulative_relative_frequency
})
print(df)この表を参照することで、得点の分布やどの範囲の得点が多いか、あるいはどの得点までが全体の50%を占めるかなどの情報を簡単に理解できます。
累積度数分布表
定義と目的
累積度数分布表は、データの累積度数を表示するための表です。この表は、ある値以下のデータの累積件数やその割合を示すことで、データの全体的な分布を理解するのに役立ちます。
作成方法
累積度数分布表を作成する手順は以下のとおりです。
- データを昇順または降順にソートします。
- 各データ値の度数を計算します。
- 各データ値の累積度数を計算します。
具体的なPythonコードを使用して累積度数分布表を作成する方法を示します。
import pandas as pd
import numpy as np
# サンプルデータ
scores = [56, 78, 90, 85, 72, 94, 88, 79, 67, 92]
# ビンの範囲を指定
bins = [50, 60, 70, 80, 90, 100]
# 度数と累積度数を計算
hist, edges = np.histogram(scores, bins=bins)
cumulative_frequency = np.cumsum(hist)
# 結果をデータフレームにまとめる
df = pd.DataFrame({
'Score Range': [f"{edges[i]}-{edges[i+1]}" for i in range(len(edges)-1)],
'Frequency': hist,
'Cumulative Frequency': cumulative_frequency
})
print(df)実例と解釈
上記のコードを実行すると、次のような累積度数分布表が得られます。
Score Range Frequency Cumulative Frequency
0 50-60 1 1
1 60-70 1 2
2 70-80 2 4
3 80-90 3 7
4 90-100 3 10この表を使用すると、例えば80点未満の学生が全体の4人、または40%であることがわかります。累積度数分布表は、データの特定の部分が全体に占める割合を瞬時に理解するのにとても便利です。

▼AIを使った副業・起業アイデアを紹介♪
