目次
データサイエンティストの必須知識、「偏微分 | 数学の基礎」について解説します。
偏微分の基礎
はじめに
多変数関数は、複数の変数を持つ関数のことを指します。例えば、ある製品の価格や品質がその売上にどれだけ影響を与えるかを知りたいときは、価格と品質の2つの変数を持つ関数を考えることができます。しかしこのような多変数関数では、一つの変数がどれだけ影響を与えるかを知るためには、他の変数を一定に保ちながら注目する変数だけを変動させてみる必要があります。このときに使用されるのが「偏微分」という手法です。
偏微分の考え方は普通の微分と似ていますが、注目する変数だけを変化させ、他の変数は一定とみなして微分します。これにより、特定の変数の変動が関数の変動にどのように影響するかを分析できます。
例: 2変数関数の偏微分
考える関数は以下のような2変数関数 \( f(x, y) \) とします。
\[
f(x, y) = x^2 + y^2
\]
この関数は、3D空間上の放物面を形成します。\( x \) または \( y \) のみが変動する場合の関数の変動を知りたいと考えます。
まず、この関数を3Dで描画してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# Define the function
def f(x, y):
return x**2 + y**2
# Create a grid of points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# Plot the 3D surface
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')
# Set the labels and title
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('f(X, Y)')
ax.set_title('Surface plot of f(x, y) = x^2 + y^2')
plt.show()
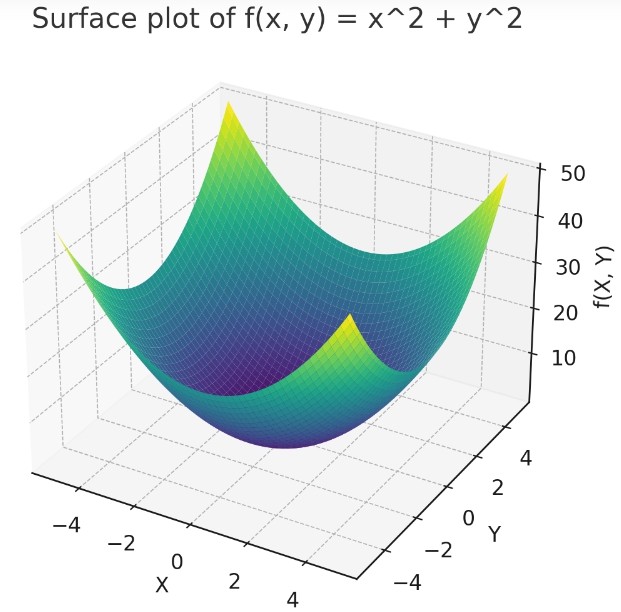
上記のグラフは、関数 \( f(x, y) = x^2 + y^2 \) の3Dの表面を示しています。この表面は放物面の形をしており、原点を中心に上向きに開いています。
偏微分を用いると、この放物面上の任意の点での傾きを、\( x \) 方向と \( y \) 方向についてそれぞれ求めることができます。具体的には、ある点での\( x \)方向の傾きはその点での\( f \)に対する\( x \)の偏微分によって、\( y \)方向の傾きはその点での\( f \)に対する\( y \)の偏微分によって求められます。
次に、この関数を \( x \) と \( y \) で偏微分して、それぞれの方向の傾きを表現してみましょう。
関数 \( f(x, y) = x^2 + y^2 \) に対して偏微分すると、次の結果を得ます。
\[
\frac{\partial f}{\partial x} = 2x
\]
\[
\frac{\partial f}{\partial y} = 2y
\]
これは関数の表面上の任意の点で、\( x \) 方向の傾きが \( 2x \) であり、\( y \) 方向の傾きが \( 2y \) であることを示しています。これにより、例えば点 \( (1,1) \) での傾きは、\( x \) 方向に2、\( y \) 方向に2であることがわかります。
偏微分はこのようにして、多変数関数の特定の方向での変動を捉えるための強力なツールとなります。さらに、この技術は物理学、経済学、工学などの多岐にわたる分野での問題解決に利用されています。
偏微分の基本的な考え方
偏微分は、多変数関数において、一つの変数のみに注目して微分する方法です。このとき、他の変数は定数として扱われます。この考え方は、3次元以上の空間で関数の動きを捉えるためにとても有用です。
例えば、平面上の点の動きを考えるとき、通常の微分を使います。しかし、3次元空間上の点の動きを考えるとき、点はx方向、y方向、z方向の3つの方向に動く可能性があります。このとき、x方向の動きだけを知りたい場合、yとzの方向の動きは無視したいと思うでしょう。この「一部の方向の動きだけを知りたい」というニーズに応えるのが偏微分です。
偏微分の記号と方法
偏微分を表すときには、特有の記号が使われます。これは、\(\frac{\partial}{\partial x}\) のように、微分記号 \(d\) の代わりに \(\partial\) を使います。この記号は、一部の変数にのみ注目して微分することを示しています。
例として、以下の2変数関数を考えます。
\[
f(x, y) = 3x^2y + 2xy + y^3
\]
この関数に対して、xに関する偏微分とyに関する偏微分を計算してみましょう。
# Define the function
f_sym = 3*x**2*y + 2*x*y + y**3
# Compute the partial derivatives
partial_x = diff(f_sym, x)
partial_y = diff(f_sym, y)
partial_x, partial_y関数 \( f(x, y) = 3x^2y + 2xy + y^3 \) に対して偏微分すると、次の結果を得ます。
\[
\frac{\partial f}{\partial x} = 6xy + 2y
\]
\[
\frac{\partial f}{\partial y} = 3x^2 + 2x + 3y^2
\]
上の式から、関数 \( f \) の \( x \) 方向の変動性は \( 6xy + 2y \) であり、\( y \) 方向の変動性は \( 3x^2 + 2x + 3y^2 \) であることがわかります。
偏微分の計算方法は、通常の微分と同じく基本的な微分のルール(和の微分、積の微分、商の微分など)を適用します。ただし、微分する変数以外の変数は定数として扱われます。
例題
以下の関数 \( g(u, v) \) について、\( u \) と \( v \) での偏微分を求めてみましょう。
\[
g(u, v) = uv^2 + \sin(uv) + e^u
\]
この例題で、偏微分の計算方法を実践的に確認してみましょう。
from sympy import sin, exp
# Correctly define the function using sympy functions
g_sym = u*v**2 + sin(u*v) + exp(u)
# Compute the partial derivatives
partial_u = diff(g_sym, u)
partial_v = diff(g_sym, v)
partial_u, partial_v
関数 \( g(u, v) = uv^2 + \sin(uv) + e^u \) に対して偏微分すると、次の結果を得ます。
\[
\frac{\partial g}{\partial u} = v^2 + v\cos(uv) + e^u
\]
\[
\frac{\partial g}{\partial v} = 2uv + u\cos(uv)
\]
これにより、関数 \( g \) の \( u \) 方向の変動性と \( v \) 方向の変動性がそれぞれ求められました。
偏微分はこのようにして、多変数関数の特定の方向での変動を捉えることができます。これは、複雑な現象やシステムを数学的に理解するための鍵となる技術です。
連鎖律と偏微分
連鎖律は、合成関数を微分する際の重要なルールです。多変数関数のコンテキストでは、連鎖律は偏微分を使用して表現され、複数の変数が関与する関数の微分を容易にします。
考え方としては、変数間の関係性を持つ複数の関数が組み合わさって新たな関数を形成する場合、この合成関数の微分は、それぞれの関数の微分の「積」によって表現されるというものです。
具体的には、関数 \( z \) が変数 \( x \) と \( y \) の関数であり、さらに \( x \) と \( y \) が別の変数 \( t \) の関数である場合、以下の連鎖律が成り立ちます。
\[
\frac{dz}{dt} = \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt}
\]
この式は、偏微分の記号を使用して合成関数の微分を表現しています。
例題: 偏微分の基本
以下の合成関数を考えます。
\[
z(t) = f(x(t), y(t))
\]
ここで、
\[
x(t) = t^2 + 1, \quad y(t) = \sin(t)
\]
\[
f(x, y) = x^2 + xy + y^2
\]
この関数 \( z(t) \) の \( t \) に関する微分を求めてみましょう。
まず、連鎖律を使用せずに直接微分する方法と、連鎖律を使用して微分する2つの方法で求め、結果を比較します。
# Define the original function f in terms of x and y
x, y = symbols('x y')
f_original = x**2 + x*y + y**2
# Compute partial derivatives of f
partial_x = diff(f_original, x)
partial_y = diff(f_original, y)
# Using the chain rule
dz_dt_chain = partial_x.subs(x, x_t) * dx_dt + partial_y.subs(y, y_t) * dy_dt
# Direct differentiation of the composite function
f_composite = f_original.subs({x: x_t, y: y_t})
dz_dt_direct = diff(f_composite, t)
dz_dt_direct, dz_dt_chain関数 \( z(t) = f(x(t), y(t)) \) の \( t \) に関する微分を2つの方法で計算した結果は次のとおりです。
- 直接の微分法:
\[
\frac{dz}{dt} = 4t(t^2 + 1) + 2t\sin(t) + (t^2 + 1)\cos(t) + 2\sin(t)\cos(t)
\] - 連鎖律を使用:
\[
\frac{dz}{dt} = 2t(2t^2 + y + 2) + (x + 2\sin(t))\cos(t)
\]
ここで、\( x = t^2 + 1 \) および \( y = \sin(t) \) です。
両方の方法で得られた結果は等しいことが確認できます。連鎖律は、合成関数の微分を簡単に計算するための強力なツールとなります。特に、多変数関数のコンテキストで微分する際には、連鎖律の使用が不可欠となります。
偏微分の応用例
偏微分は、複数の変数を持つ関数の特定の方向での変動を理解するためのツールとして広く利用されています。以下は、その応用例の一部です。
1. 経済学:
コスト関数や利益関数は、多くの場合、複数の入力変数(例えば、生産量や広告費)に依存します。これらの関数の偏微分(または偏導関数)は、特定の入力変数の変化が全体のコストや利益にどれだけの影響を与えるかを示します。これを「限界コスト」や「限界利益」と呼びます。
2. 物理学:
熱伝導や流体力学などの多くの物理的現象は、偏微分方程式を用いて記述されます。これらの方程式は、空間の特定の方向での変動や時間に対する変動を考慮して、物理的現象をモデル化します。
3. 機械学習:
機械学習のアルゴリズム、特にニューラルネットワークの訓練において、コスト関数(または損失関数)の偏微分は、モデルのパラメータを最適化するための指針として使用されます。これは「勾配降下法」として知られています。
例題: 経済学の応用
ある企業の利益関数が以下のように与えられるとします。
\[
P(x, y) = 100x + 50y – x^2 – y^2
\]
ここで、\( x \) は生産される製品Aの数量、\( y \) は生産される製品Bの数量です。この利益関数に対して、製品Aおよび製品Bの生産量の変化が利益に与える影響を求めてみましょう。
# Define the profit function
P = 100*x + 50*y - x**2 - y**2
# Compute the partial derivatives
partial_x = diff(P, x)
partial_y = diff(P, y)
partial_x, partial_y利益関数 \( P(x, y) = 100x + 50y – x^2 – y^2 \) に対する偏微分を計算すると、以下の結果を得ます。
\[
\frac{\partial P}{\partial x} = 100 – 2x
\]
\[
\frac{\partial P}{\partial y} = 50 – 2y
\]
上の式から、製品Aの生産量 \( x \) が1単位増加すると、利益は \( 100 – 2x \) 単位増加することがわかります。同様に、製品Bの生産量 \( y \) が1単位増加すると、利益は \( 50 – 2y \) 単位増加することがわかります。
このように、偏微分を使用して、各入力変数の変化が関数の出力に与える影響を量的に評価できます。

▼AIを使った副業・起業アイデアを紹介♪
