データサイエンティストの必須知識、「幾何ベクトル | 数学の基礎」について解説します。
幾何ベクトルの基礎
幾何ベクトルは、大きさと方向を持つ量を表現するための数学的なツールです。物理的には、力や速度などのベクトル量を表現するのに使用されます。幾何学的には、空間内の2点間の位置関係や移動を示すのに役立ちます。
ベクトルの基本的な定義
ベクトルを理解するための基本的な定義や概念を以下に示します。
ベクトルの起点と終点
ベクトルは矢印で表現され、その始点を「起点」、終点を「終点」と呼びます。起点と終点の位置によってベクトルは定義されますが、ベクトルの大きさや方向が同じであれば、どこに描かれているかは問いません。
例: 平面上の2点 \( A(1, 2) \) と \( B(4, 6) \) があるとき、点 \( A \) から点 \( B \) へのベクトルを \( \mathbf{AB} \) と書きます。
import matplotlib.pyplot as plt
# Points A and B
A = (1, 2)
B = (4, 6)
plt.quiver(A[0], A[1], B[0]-A[0], B[1]-A[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(0, 5)
plt.ylim(0, 7)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Vector AB')
plt.grid(True)
plt.show()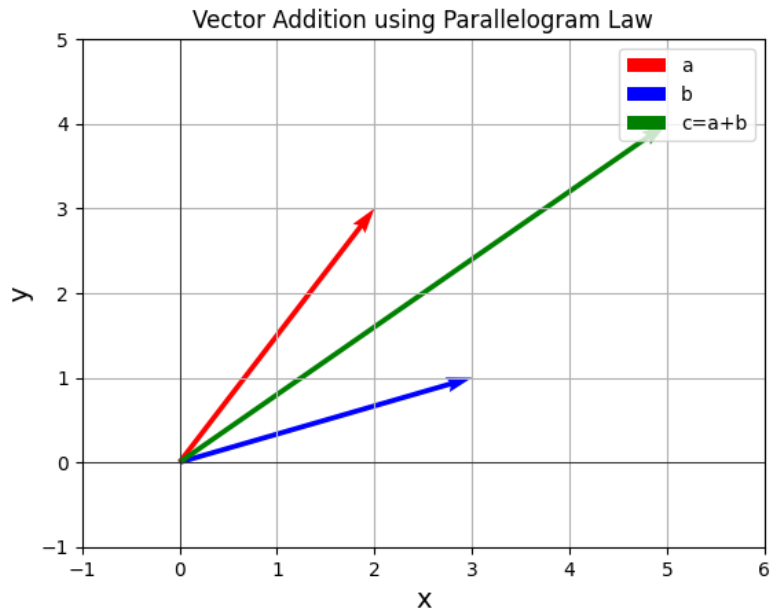
上のグラフでは、点 \( A \) から点 \( B \) へのベクトル \( \mathbf{AB} \) が赤い矢印で示されています。
ベクトルの大きさ
ベクトルの大きさは、その長さを示し、通常「ノルム」としても知られています。2点間のベクトルの大きさは、2点間の距離として計算できます。
例: ベクトル \( \mathbf{AB} \) の大きさは、ピタゴラスの定理を使用して以下のように計算できます。
\[
|\mathbf{AB}| = \sqrt{(B_x – A_x)^2 + (B_y – A_y)^2}
\]
import math
# Calculate the magnitude of vector AB
magnitude_AB = math.sqrt((B[0]-A[0])**2 + (B[1]-A[1])**2)
magnitude_AB方向
ベクトルの方向は、その矢印の向きによって示されます。平面上のベクトルの方向は、通常、x軸との間の角度で示されます。
例: ベクトル \( \mathbf{AB} \) の方向は、以下のように計算できます。
\[
\theta = \tan^{-1}\left(\frac{B_y – A_y}{B_x – A_x}\right)
\]
# Calculate the direction of vector AB
direction_AB = math.atan2(B[1]-A[1], B[0]-A[0])
direction_AB_in_degrees = math.degrees(direction_AB)
direction_AB_in_degrees幾何ベクトルは空間内の物体や点の動きや関係を数学的に表現するのにとても便利です。基本的な定義や概念を理解することで、ベクトルの計算や応用が容易になります。
ベクトルの表現方法
ベクトルを理解するための基本的なステップの一つは、その「表現方法」です。ベクトルは方向と大きさを持つ量であり、これをどのように表現するかはとても重要です。ここでは、2つの主な表現方法、すなわち「成分表示」と「方向コサイン」について解説します。
成分表示
成分表示は、ベクトルをその成分に分解して表示する方法です。3次元空間におけるベクトルを考えた場合、このベクトルはx、y、zの3つの方向にそれぞれの成分を持っています。このベクトルを\(\mathbf{v}\)とすると、成分表示では以下のように表されます。
\[
\mathbf{v} = \begin{bmatrix} v_x \ v_y \ v_z \end{bmatrix}
\]
ここで、\(v_x\)、\(v_y\)、\(v_z\)はそれぞれx、y、z方向の成分を示しています。
例えば、ベクトル\(\mathbf{v}\)が3次元空間での点A(2, 3, 4)から原点O(0, 0, 0)へのベクトルである場合、このベクトルの成分表示は以下のようになります。
\[
\mathbf{v} = \begin{bmatrix} 2 \ 3 \ 4 \end{bmatrix}
\]
方向コサイン
方向コサインは、ベクトルの方向を示すものです。具体的には、ベクトルと各座標軸との間の角度のコサインの値を取ります。ベクトル\(\mathbf{v}\)とx、y、z軸との間の角度をそれぞれ\(\alpha\)、\(\beta\)、\(\gamma\)とすると、方向コサインは以下のように表されます。
\[
\cos(\alpha) = \frac{v_x}{|\mathbf{v}|}
\]
\[
\cos(\beta) = \frac{v_y}{|\mathbf{v}|}
\]
\[
\cos(\gamma) = \frac{v_z}{|\mathbf{v}|}
\]
ここで、\( |\mathbf{v}| \)はベクトル\(\mathbf{v}\)の大きさを示しています。
方向コサインは、ベクトルの方向を定量的に示すことができるため、ベクトルの方向を知る際にとても有用です。
ベクトルの表現方法には、成分表示と方向コサインの2つの主な方法があります。成分表示はベクトルをその成分に分解して表示する方法であり、方向コサインはベクトルの方向を示す方法です。これらの表現方法を理解することで、ベクトルの性質や操作をより深く理解できます。
ベクトルの演算
ベクトルの加算と減算
ベクトルの加算と減算は、物理的な現象や空間内の移動を表現する際にとても有用です。例えば、2つの力が物体に作用するとき、その結果としての合成力を知りたい場合や、2つの移動の結果を知りたい場合などに使用します。ベクトルの加算と減算には、平行四辺形の法則と三角法則がよく使われます。
平行四辺形の法則
ベクトルの加算は、2つのベクトルを並べて平行四辺形を形成し、その対角線が2つのベクトルの和となるという法則です。
数式で表すと、ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の和 \( \mathbf{c} \) は以下のようになります。
\[ \mathbf{c} = \mathbf{a} + \mathbf{b} \]
以下のPythonコードは、この法則をグラフ上に描画するものです。
import matplotlib.pyplot as plt
import numpy as np
# ベクトルaとbを定義
a = np.array([2, 3])
b = np.array([3, 1])
# ベクトルの加算
c = a + b
# グラフに描画
plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1, color='r', label="a")
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color='b', label="b")
plt.quiver(0, 0, c[0], c[1], angles='xy', scale_units='xy', scale=1, color='g', label="c=a+b")
# グリッドを描画
plt.grid()
plt.axvline(0, color='black',linewidth=0.5)
plt.axhline(0, color='black',linewidth=0.5)
plt.xlim(-1, 6)
plt.ylim(-1, 5)
plt.xlabel('x', size=14)
plt.ylabel('y', size=14)
plt.title('Vector Addition using Parallelogram Law')
plt.legend()
plt.show()三角法則
三角法則は、2つのベクトルの始点を合わせて、ベクトルを順番に結んで三角形を作ったとき、3番目の辺が2つのベクトルの差となるという法則です。
数式で表すと、ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の差 \( \mathbf{d} \) は以下のようになります。
\[ \mathbf{d} = \mathbf{a} – \mathbf{b} \]
例題:
ベクトル \( \mathbf{a} = \begin{bmatrix} 3 \ 4 \end{bmatrix} \) と \( \mathbf{b} = \begin{bmatrix} 1 \ 2 \end{bmatrix} \) が与えられたとき、\( \mathbf{a} – \mathbf{b} \) を求めなさい。
解答:
\[ \mathbf{a} – \mathbf{b} = \begin{bmatrix} 3 – 1 \ 4 – 2 \end{bmatrix} = \begin{bmatrix} 2 \ 2 \end{bmatrix} \]
これらの法則を利用すると、ベクトルの加算や減算が直感的に理解しやすくなります。ベクトルの基本的な操作を理解することは、幾何学や物理学などのさまざまな分野での応用を可能にします。
ベクトルのスカラー倍
ベクトルのスカラー倍は、ベクトルをある実数倍する操作を指します。具体的には、ベクトル \( \mathbf{a} \) に対して、スカラー \( k \) でスカラー倍を行うと、ベクトルの各成分が \( k \) 倍されることを意味します。
数式で表すと、ベクトル \( \mathbf{a} = [a_1, a_2] \) のスカラー \( k \) 倍は
\[
k\mathbf{a} = [ka_1, ka_2]
\]
となります。
例:
ベクトル \( \mathbf{a} = [2, 3] \) を3倍する場合、
\[ 3\mathbf{a} = [6, 9] \]
となります。
内積
内積は、2つのベクトルがどれだけ同じ方向を向いているかを示す量です。具体的には、2つのベクトルの成分をそれぞれ掛け合わせて合計したものを指します。
内積の公式
2つのベクトル \( \mathbf{a} = [a_1, a_2] \) および \( \mathbf{b} = [b_1, b_2] \) の内積は次のように定義されます:
\[
\mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2
\]
例:
ベクトル \( \mathbf{a} = [2, 3] \) と \( \mathbf{b} = [4, 1] \) の内積は、
\[ \mathbf{a} \cdot \mathbf{b} = 2 \times 4 + 3 \times 1 = 8 + 3 = 11 \]
となります。
内積と角度
2つのベクトルの内積は、それらのベクトルの間の角度とも関係しています。具体的には、次の公式で表されます:
\[
\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos(\theta)
\]
ここで、\( |\mathbf{a}| \) および \( |\mathbf{b}| \) はそれぞれベクトル \( \mathbf{a} \) および \( \mathbf{b} \) の大きさを示し、\( \theta \) はベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の間の角度を示します。
この公式を使用すると、2つのベクトルの間の角度を計算できます。具体的には、
\[
\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}
\]
となります。
例:
先ほどのベクトル \( \mathbf{a} = [2, 3] \) および \( \mathbf{b} = [4, 1] \) の間の角度を求める場合、まず内積を求め、次にベクトルの大きさを求めて、上記の公式を使用します。
外積(クロス積)
外積、またはクロス積、は、ベクトル演算の一つで、2つのベクトルの間で定義される演算です。この演算の結果は、新しいベクトルとなります。外積の特徴として、結果となるベクトルは、2つの元となるベクトルのどちらとも直交するという性質を持っています。
外積の計算方法
3次元のベクトル \( \mathbf{a} = [a_1, a_2, a_3] \) と \( \mathbf{b} = [b_1, b_2, b_3] \) の外積 \( \mathbf{a} \times \mathbf{b} \) は以下のように計算されます。
\[
\mathbf{a} \times \mathbf{b} = \left[ \begin{array}{c}
a_2b_3 – a_3b_2 \
a_3b_1 – a_1b_3 \
a_1b_2 – a_2b_1 \
\end{array} \right]
\]
例:
ベクトル \( \mathbf{a} = [1, 2, 3] \) と \( \mathbf{b} = [4, 5, 6] \) の外積を計算すると、以下のようになります。
\[
\mathbf{a} \times \mathbf{b} = [-3, 6, -3]
\]
外積の物理的意味
外積の結果として得られるベクトルの大きさは、2つのベクトルが成す平行四辺形の面積に等しくなります。これは、外積が2つのベクトルの「幾何的な関係性」を分析できることを意味しています。
また、外積の方向は、右手の法則によって決定されます。具体的には、ベクトル \( \mathbf{a} \) の方向からベクトル \( \mathbf{b} \) の方向へ指を曲げると、親指が指す方向が外積の方向となります。
物理的応用:
外積は物理学の中で、特に力学の分野で頻繁に使用されます。例えば、トルク(回転を生じる力のモーメント)は、位置ベクトルと力ベクトルの外積として表されます。
Pythonでの外積の計算
PythonのNumPyライブラリを使用すると、外積の計算はとても簡単に実行できます。以下に例を紹介します。
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
cross_product = np.cross(a, b)
print(cross_product)このコードを実行すると、[-3, 6, -3] という結果が得られます。
ベクトルの応用
ベクトルと直線
ベクトルは、空間内の直線や平面を表現するための強力なツールとして使用されます。ここでは、ベクトルを使用して直線を表現する方法や、点と直線との距離を求める方法について考察します。
直線の方程式
空間内の直線は、1つの点とその直線上の方向を示すベクトルによって一意に定義されます。ある点 \( \mathbf{p} = [p_1, p_2, p_3] \) を通り、方向ベクトル \( \mathbf{d} = [d_1, d_2, d_3] \) を持つ直線の方程式は次のように表されます。
\[
\mathbf{r}(t) = \mathbf{p} + t\mathbf{d}
\]
ここで、\( t \) はスカラーパラメータであり、この値を変えることで直線上の異なる点を得られます。
例:
点 \( \mathbf{p} = [1, 2, 3] \) を通り、方向ベクトル \( \mathbf{d} = [2, 1, 0] \) を持つ直線の方程式は、
\[
\mathbf{r}(t) = [1 + 2t, 2 + t, 3]
\]
となります。
点と直線の距離
点 \( \mathbf{a} \) と直線 \( \mathbf{r}(t) \) との距離を求めるには、点 \( \mathbf{a} \) から直線に下ろした垂線の長さを計算します。この距離は以下の公式で与えられます。
\[
d = \frac{|\mathbf{a} – \mathbf{p} \times \mathbf{d}|}{|\mathbf{d}|}
\]
ここで、\( \times \) は外積を示し、\( |\mathbf{d}| \) は方向ベクトル \( \mathbf{d} \) の大きさを示します。
例:
点 \( \mathbf{a} = [4, 5, 6] \) と、先ほどの直線 \( \mathbf{r}(t) \) との距離を求めるには、上記の公式を使用して計算します。
PythonのNumPyライブラリを使用してこの距離を計算する方法を以下に示します。
import numpy as np
# 定義されたベクトル
a = np.array([4, 5, 6])
p = np.array([1, 2, 3])
d = np.array([2, 1, 0])
# 距離の計算
distance = np.linalg.norm(np.cross(a - p, d)) / np.linalg.norm(d)
print(distance)このコードを実行すると、点と直線の距離が計算されます。
ベクトルと平面
ベクトルは、空間における平面を表現したり、平面上の点や他の平面との関係を解析するためのツールとしても使用されます。特に、空間の任意の点と平面との距離を求める際にベクトルはとても役立ちます。
平面の方程式
空間内の平面は、1つの点とその平面の法線ベクトル(平面と垂直な方向を示すベクトル)によって一意に定義されます。ある点 \( \mathbf{p} = [p_1, p_2, p_3] \) を通り、法線ベクトル \( \mathbf{n} = [n_1, n_2, n_3] \) を持つ平面の方程式は次のように表されます。
\[
n_1(x – p_1) + n_2(y – p_2) + n_3(z – p_3) = 0
\]
この方程式は、平面上の任意の点 \( (x, y, z) \) に対して成り立ちます。
例:
点 \( \mathbf{p} = [1, 2, 3] \) を通り、法線ベクトル \( \mathbf{n} = [2, 2, 1] \) を持つ平面の方程式は、
\[
2(x – 1) + 2(y – 2) + (z – 3) = 0
\]
となります。
点と平面の距離
点 \( \mathbf{a} = [a_1, a_2, a_3] \) と平面の距離は、以下の公式を使用して計算されます。
\[
d = \frac{|n_1(a_1 – p_1) + n_2(a_2 – p_2) + n_3(a_3 – p_3)|}{\sqrt{n_1^2 + n_2^2 + n_3^2}}
\]
例:
点 \( \mathbf{a} = [4, 5, 6] \) と、先ほどの平面との距離を求めるには、上記の公式を使用して計算します。
PythonのNumPyライブラリを使用してこの距離を計算する方法を以下に示します。
import numpy as np
# 定義されたベクトルと点
a = np.array([4, 5, 6])
p = np.array([1, 2, 3])
n = np.array([2, 2, 1])
# 距離の計算
distance = abs(np.dot(n, (a - p))) / np.linalg.norm(n)
print(distance)このコードを実行すると、点と平面の距離が計算されます。
ビジネスでのベクトルの応用
ベクトルの概念は、数学や物理だけでなく、ビジネスでも重要な役割を果たしています。特に、データ分析や機械学習の分野でのベクトルの利用は、企業の意思決定や戦略に中心的な役割を担っています。
- データ表現: ビジネスのデータは、顧客の購買履歴、製品の特性、市場の動向など、多様な情報から構成されています。これらの情報をベクトルとして表現することで、数学的な手法を用いて解析や予測できます。
- 類似性の計測: 顧客の購買傾向や製品の特性をベクトルで表現した場合、ベクトル間の距離や角度を計算することで、その類似性や関連性を定量的に評価できます。これは、製品の推薦や顧客のセグメンテーションなど、多くのビジネスアプリケーションに応用されています。
- 最適化問題: ビジネスの多くの課題は、利益を最大化するような戦略や、コストを最小化するような生産計画を立てることなど、最適化問題として分析できます。ベクトルを用いてこれらの問題を数学的に定式化し、解を求めることが可能です。
例: 商品の推薦システムでは、ユーザーの過去の購買履歴をベクトルとして表現し、そのベクトルと商品の特性を表すベクトルとの間の内積を計算することで、ユーザーの興味や好みに合った商品を推薦できます。
まとめ
ベクトルは、幾何学的な形や物体の動きを表現するための基本的なツールとして、古くから使用されてきました。しかし、データ駆動型のビジネスの発展に伴い、ベクトルの概念はデータ分析や機械学習の分野での重要性を増しています。
ベクトルの理解は、現代のビジネスや技術の多くの分野での成功を支える基盤です。

▼AIを使った副業・起業アイデアを紹介♪
