目次
データサイエンティストの必須知識、「勾配消失問題 | ディープラーニングの基礎」について解説します。
勾配消失問題とは
勾配消失問題の概要
勾配消失問題とは
勾配消失問題は、ディープラーニングのモデル(特に深いニューラルネットワーク)で学習中に、勾配がとても小さくなってしまう現象を指します。この問題が発生すると、ネットワークの重みが十分に更新されなくなり、学習が進行しづらくなります。
勾配消失が問題となる理由
ニューラルネットワークの学習は、勾配降下法を基にしています。このため、勾配が小さくなると重みの更新がほとんど行われなくなり、学習が停滞してしまいます。特に、深いネットワークでは多くの層を通過する間に勾配が小さくなるため、勾配消失問題が顕著に現れやすくなります。
\[
\text{更新される重み} \propto \text{勾配}
\]
上記の数式から、勾配が0に近づくと、重みの更新量も0に近づくことが分かります。
勾配消失が発生する状況
主な勾配消失の原因は以下の通りです。
- 活性化関数の選択: シグモイドやハイパボリックタンジェントなどの活性化関数は、入力の絶対値が大きい場合、出力の勾配がとても小さくなります。
- 重みの初期化: 適切でない重みの初期化は、学習初期から勾配が小さくなる原因となります。
- ネットワークの深さ: ネットワークが深いと、多くの層を通過する間に勾配が小さくなりやすいです。
例として、シグモイド関数のグラフを考えると、入力の絶対値が大きくなると出力が0または1に飽和して勾配はほぼ0になります。これが、勾配消失の一因となります。
勾配消失問題の原因
活性化関数の選択
勾配消失問題の一つの大きな原因は、活性化関数の選択にあります。特にシグモイド関数やハイパボリックタンジェント関数(tanh)は、入力の絶対値が大きくなると出力が飽和し、勾配がとても小さくなります。
\[
\text{シグモイド関数}:f(x) = \frac{1}{1 + e^{-x}}
\]
\[
\text{tanh関数}:f(x) = \tanh(x)
\]
これらの関数は、初期のディープラーニングモデルでよく使用されていましたが、ネットワークが深くなるにつれて勾配消失問題が顕著になりました。
重みの初期化方法
重みの初期化方法も勾配消失問題の原因となり得ます。例えば、すべての重みを0で初期化すると、学習が進行しなくなります。また、重みがとても小さい値で初期化されると、勾配が小さくなりやすいです。
適切な初期化方法を使用することで、勾配消失問題を軽減できます。例えば、He初期化やXavier初期化などが、ReLUやtanhなどの特定の活性化関数と組み合わせて使用されることが多いです。
深いネットワークの影響
ネットワークが深い場合、特にシグモイド関数やtanh関数を使用している場合、多くの層を通過する間に勾配がどんどん小さくなる可能性があります。これは各層での勾配が乗算されるため、勾配が連続して小さくなると最終的にとても小さい勾配となってしまいます。
深いネットワークを訓練する際には、特に勾配消失問題に注意が必要です。これを解決するための技術や手法も多く提案されています。その中でもReLUやその派生関数、適切な重みの初期化、バッチ正規化などが実践的に使用されることが多いです。
勾配消失問題の解決策
ReLUとその派生関数
ReLU(Rectified Linear Unit)は、非線形活性化関数の一つで、以下の式で定義されます。
\[
f(x) = \max(0, x)
\]
ReLUは、正の入力に対してそのままの出力を返し、負の入力に対しては0を返すという特性があります。これにより、勾配消失問題を大幅に軽減できます。
しかしながら、ReLUには負の入力に対して常に0の勾配を持ってしまうという「死んだReLU」という問題があります。これを解決するための派生関数として、Leaky ReLUやParametric ReLU、Exponential Linear Units (ELU)などが提案されています。
適切な重みの初期化
重みの初期化方法は、勾配消失問題や勾配爆発問題の発生を抑える上でとても重要です。特に、Xavier初期化やHe初期化は、特定の活性化関数との組み合わせで効果的です。
- Xavier初期化: tanhやシグモイド関数との組み合わせで使用することが推奨されます。
- He初期化: ReLUやその派生関数との組み合わせで使用することが推奨されます。
バッチ正規化
バッチ正規化は、各層の入力の分布を正規化することで、勾配消失問題や勾配爆発問題を軽減する手法です。具体的には、ミニバッチごとの平均と分散を計算し、それを用いて入力を正規化します。この手法により、学習が安定し、学習率を大きく設定できます。
勾配クリッピング
勾配クリッピングは、勾配の大きさが一定の値を超えた場合に、それを制限する手法です。これにより、勾配爆発問題を回避できます。具体的には、勾配のL2ノルムが一定のしきい値を超える場合、勾配をスケーリングしてその大きさを制限します。
# Gradient clipping example using TensorFlow
gradients, variables = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0) # Clip gradients by L2 norm
train_op = optimizer.apply_gradients(zip(gradients, variables))上記の例では、TensorFlowを使用して、勾配のL2ノルムが5を超えないように勾配をクリッピングしています。
実例と実験
勾配消失問題の実例
勾配消失問題は、特に深いニューラルネットワークでよく発生します。シグモイド関数やtanh関数を活性化関数として用いた多層のニューラルネットワークでこの問題が顕著に現れます。例として、10層以上の深さを持つニューラルネットワークを考えると、初期の学習段階での勾配の大きさがとても小さくなってしまう現象が観察されることが多いです。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数とその導関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
x = np.random.randn(10, 2) # 10個のデータ
node_num = 5 # 各隠れ層のノード(ニューロン)の数
hidden_layer_size = 5 # 隠れ層が5層
activations = {} # ここにアクティベーションの結果を格納する
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(x.shape[1], node_num) * 1
z = np.dot(x, w)
a = sigmoid(z)
activations[i] = a
# ヒストグラムを描画
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()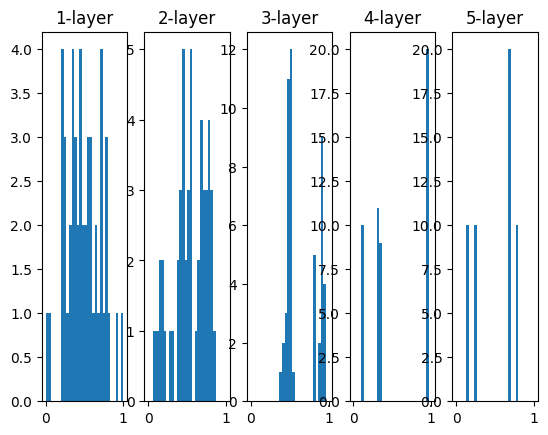
このコードは、5層のニューラルネットワークにおける各層のアクティベーションの分布を示すヒストグラムを描画します。シグモイド関数の性質から、アクティベーションが0や1に偏ると、その層の勾配の大きさがとても小さくなることがわかります。
解決策の効果の比較実験
解決策の効果を実感するための実験として、以下のシナリオを考えます。
- 活性化関数をシグモイド関数とReLUで変更して学習し、学習の進行具合を比較します。
- 重みの初期化方法をさまざまに変えて学習し、その影響を観察します。
- バッチ正規化を導入したネットワークとそうでないネットワークでの学習速度を比較します。
これらの実験を通じて、勾配消失問題への対策の効果を実感できます。
まとめ
勾配消失問題は、ディープラーニングの学習において重要な課題の一つです。この問題を理解し、適切な手法を選択することで、効果的な学習が可能となります。

▼AIを使った副業・起業アイデアを紹介♪
