決定木 | 機械学習の基礎

決定木の基礎

定義と概要

決定木は、機械学習の手法の一つで、データを分類あるいは回帰するためのモデルです。名前の通り、木構造を持ち、各ノードで特定の属性に基づいてデータを分割します。最終的に、各葉ノードが一つの予測結果に対応します。

決定木の最も大きな特徴は、生成されたモデルがとても直感的であることです。人間が手で作成するルールベースの判定ロジックととても似ているため、どのように予測が行われるのかを視覚的に理解しやすいです。このため、ビジネスの現場などで、モデルの説明や理解が必要な場面でよく使用されます。

決定木の特徴

  1. 直感的なモデル: 木構造のモデルは、人間が理解しやすい形式であるため、なぜある予測がされたのかを説明するのが容易です。
  2. データの前処理が少ない: 多くの機械学習アルゴリズムでは、特徴量のスケーリングや欠損値の取り扱いなどデータの前処理が必要ですが、決定木はこれらの前処理を最小限に抑えることができます。
  3. 非線形データにも適用可能: 線形分離が不可能なデータでも、決定木を使用することで適切に分類できます。
  4. 分類と回帰の両方に使用可能: ターゲット変数が連続値の場合やカテゴリ値の場合の両方で使用できます。

ただし、決定木には過学習しやすいという欠点もあります。深い木が生成されると、訓練データにはとても適合するものの、新しいデータにはうまく適合しないという問題が生じることがあります。この問題を解決するための方法として、枝刈りやランダムフォレストなどのアンサンブル手法が存在します。

決定木の動作原理

分割の基準

決定木は、データを再帰的に分割することで学習します。この際、どの特徴を使い、どの値で分割するかを決める基準が必要です。以下は、その基準としてよく用いられるものたちです。

エントロピー

エントロピーは、データの不純度を示す指標の一つで、以下の数式で表されます。

\[
E(p) = -p \log_2(p) – (1-p) \log_2(1-p)
\]

ここで、\( p \)は正例の割合を示します。エントロピーは0から1の間の値を取り、値が高いほどデータの不純度が高い、すなわち混在度が高いことを示します。

ジニ不純度

ジニ不純度も、データの不純度を示す指標の一つです。以下の数式で表されます。

\[
G(p) = 2p(1-p)
\]

この指標も0から1の間の値を取り、値が高いほどデータの混在度が高いことを示します。

情報利得

情報利得は、ある属性による分割前後のエントロピーの差として定義されます。分割によってどれだけ不純度が減少したかを示す指標となります。

\[
IG(p) = E(p_{\text{before}}) – E(p_{\text{after}})
\]

情報利得が最大となる属性とその値で分割を行うのが、決定木の基本的な動作原理です。

再帰的分割

決定木は、上記の基準を用いてデータを再帰的に分割します。分割は、情報利得が最大となる属性とその値で行われます。分割を繰り返すことで、木構造のモデルが形成されるわけです。

枝刈り

決定木の学習を行うと、過学習を起こすことがあります。これは、訓練データに対しては高い精度を示すものの、新しいデータに対しては低い精度となる状態を指します。過学習を防ぐための手法として、枝刈りがあります。これは、木の深さを制限することや、情報利得がある閾値以下の分割を行わないといった方法が考えられます。

決定木のメリット・デメリット

メリット

  1. 直感的な理解が可能：決定木は「もし〜ならば」というルールに基づいているため、人間が直感的に理解しやすい。
  2. データの前処理が少ない：多くの場合、欠損値の取り扱いや特徴のスケーリングなどの前処理をあまり必要としない。
  3. カテゴリカルデータの取り扱い：カテゴリカルなデータも直接扱うことができる。
  4. 可視化が容易：決定過程を木構造として可視化でき、モデルの解釈がしやすい。

デメリット

  1. 過学習しやすい：深い木を作りすぎると訓練データに過度に適合してしまう。
  2. 安定性の欠如：データの小さな変更で構造が大きく変わることがある。
  3. 最適な決定木の探索がNP完全問題：最も良い木を効率的に探索することは難しい。
  4. 線形性の扱い：線形の関係性を捉えるのが難しく、線形モデルよりも多くのノードを必要とする場合がある。

ランダムフォレストとの関連性

ランダムフォレストは、複数の決定木を組み合わせて動作するアンサンブル学習の一つです。ランダムフォレストは以下の特徴を持ちます。

  1. バギング：訓練データのサブセットをランダムに選び、それぞれのサブセットで決定木を訓練します。
  2. 特徴量のランダムサブセット：分割の際に全ての特徴量ではなく、ランダムに選ばれたサブセットの中から最適な特徴量を選びます。
  3. 過学習の低減：複数の決定木の平均を取ることで、個々の決定木の過学習の影響を低減します。
  4. 高い予測精度：多くの実際のデータセットで、単一の決定木よりも高い予測精度を示すことが多い。

ランダムフォレストは、決定木の多くのデメリットを克服するために設計された方法です。特に、過学習の問題を軽減する手法として人気があります。

過学習とは？

過学習（Overfitting）は、機械学習モデルが訓練データに対して高い精度を示す一方で、新しいデータ（テストデータ）に対しては低い精度を示す現象を指します。言い換えれば、モデルが訓練データのノイズやランダムな変動まで学習してしまうため、一般化能力が低くなることを意味します。

過学習の原因と対策

データの不足

原因：
データの量が少ない場合、モデルはデータ内のランダムなノイズを学習してしまいやすくなります。

対策：

  1. さらに多くのデータを収集する。
  2. データを拡張する（例：画像データの場合、回転や拡大・縮小などで新しいデータを生成する）。

枝刈りによる対策

原因：
決定木が深くなりすぎると、訓練データに対してのみ高い精度を持つようになります。これは、木が訓練データの細かい特徴までキャッチしてしまうためです。

対策：

  1. 枝刈り（Pruning）を行う。これは、決定木がある深さに達したら成長を停止させる技法です。
  2. 木の最大深さを制限する。
  3. ノードが分割する際の最小サンプル数を設定する。

Pythonのコード例:

from sklearn.tree import DecisionTreeClassifier

# モデルのインスタンス化
clf = DecisionTreeClassifier(max_depth=3, min_samples_split=10)

# モデルの訓練
clf.fit(X_train, y_train)

# 予測
predictions = clf.predict(X_test)

このコードは、決定木の最大の深さを3、そしてノードが分割する際の最小サンプル数を10として制限しています。これにより、過学習を防ぐ可能性が高まります。

過学習は機械学習の中でも特に重要なテーマであり、理解し、対策することが重要です。

実際の利用シーン

決定木はその直感的な解釈可能性から、多くの業界や問題に利用されています。以下にいくつかの具体的な利用シーンと事例を紹介します。

業界別の利用事例

  1. 医療：病気の診断において、患者の症状や検査結果を入力として、特定の病気のリスクを評価する。
  2. 金融：顧客の信用スコアリングやローンの承認。顧客の過去の取引履歴や収入情報などから、信用リスクを評価する。
  3. マーケティング：顧客の購入履歴やアクセス履歴などのデータを基に、将来の購入確率や顧客のセグメント化を行う。
  4. 製造業：製品の品質検査や不良品の発見。センサーデータや製造過程の情報を用いて、製品の品質を評価する。

問題への適用

  1. タイタニック号の生存者予測：タイタニック号の乗客データ（年齢、性別、乗船クラスなど）を使用して、乗客が生存したかどうかを予測する。これは、データサイエンスの入門問題としても知られている。

Pythonのコード例:

# 必要なライブラリのインポート
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# データの準備
titanic_data = pd.read_csv('path_to_titanic_data.csv')
X = titanic_data.drop('Survived', axis=1)
y = titanic_data['Survived']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)

# 予測
y_pred = clf.predict(X_test)

# 評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
  1. 花の分類：アヤメのデータセットを使用して、花の種類を分類する。アヤメのデータセットは、花の大きさや形状の情報を持っており、これを基に3つの異なる種類のアヤメを分類する。

決定木は、上記のような多様な業界や問題において、その解釈の容易さと効果的な予測性能から広く利用されています。決定木の基本的な概念や動作原理を理解することで、多くの問題への適用が可能となります。

Pythonでの実装方法

Pythonを使用した決定木の実装はとても簡単で、scikit-learnというライブラリを使用します。以下に、その手順を説明します。

必要なライブラリのインポート

まず、決定木の実装に必要なライブラリをインポートします。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

データの準備

ここでは、scikit-learnが提供しているアヤメのデータセットを使用します。このデータセットには、3つの異なるアヤメの種類が150サンプル含まれています。

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

モデルの訓練

次に、決定木のモデルを訓練します。

clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)

予測と評価

モデルの訓練が終わったら、テストデータを使って予測し、その精度を評価します。

y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

決定木の可視化

決定木の大きなメリットの一つは、その構造を可視化しやすいことです。以下のコードを使用すると、訓練した決定木の構造を可視化できます。

import graphvizfrom sklearn.tree import export_graphvizdot_data = export_graphviz(clf, out_file=None,                            feature_names=iris.feature_names,                             class_names=iris.target_names,                             filled=True, rounded=True,                             special_characters=True)  graph = graphviz.Source(dot_data)  graph.render("iris_tree")  # これにより、"iris_tree.pdf"という名前のファイルが生成されます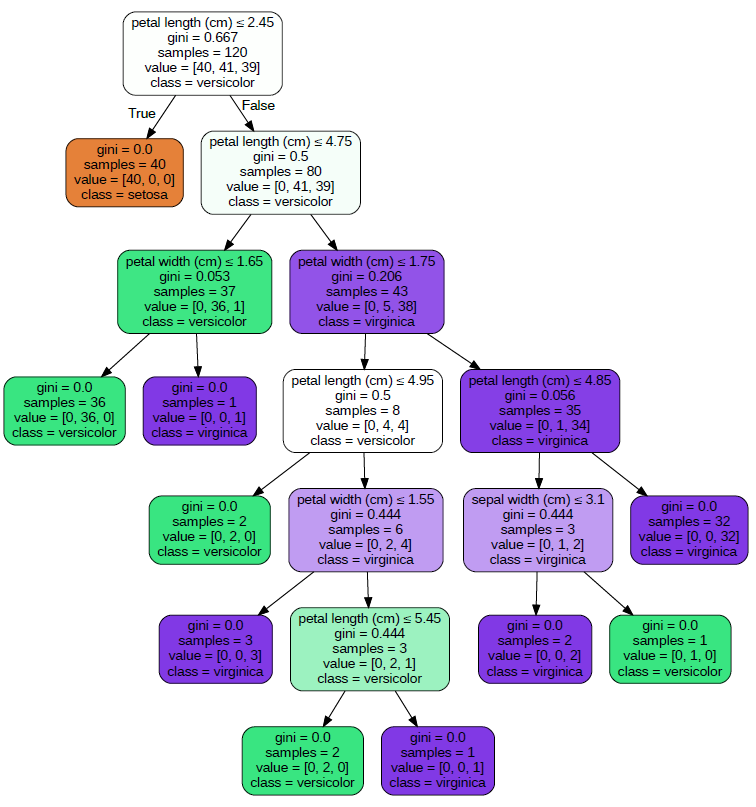
訓練した決定木の構造を可視化する

まとめ

決定木は、その解釈の容易さと直感的な構造から多くの実世界の問題に適用されています。Pythonのscikit-learnライブラリを使って、簡単に決定木を実装し、評価できます。

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


前の記事

サポートベクターマシン | 機械学習の基礎

次の記事

アンサンブル学習 | 機械学習の基礎