k近傍(k-NN)法とk平均(k-means)法 | 機械学習の基礎

k近傍(k-NN)法とは？

基本的な概念

k近傍法 (k-NN) は、分類および回帰の問題に利用される単純なアルゴリズムの1つです。名称の「k近傍」は、あるデータ点の「近傍」のデータ点を「k」個取り上げることから名付けられました。k近傍法の特徴はトレーニングデータをモデルとして直接利用する「インスタンスベースの学習」である点です。

アルゴリズムの流れ

1. 予測したいデータ点とトレーニングデータ内の全てのデータ点との距離を計算します。
2. 距離が最も近いk個のデータ点を選びます。
3. 分類の場合: k個のデータ点の中で最も多いカテゴリを予測結果として選びます。
4. 回帰の場合: k個のデータ点の平均値や中央値を予測結果として選びます。

kの選び方とその重要性

kの値によって、k近傍法の性能は大きく変わる可能性があります。小さいkの値（例えば1）を選ぶと、ノイズに弱くなり過学習のリスクが高まります。一方、大きいkの値を選ぶと決定境界が滑らかになりモデルが単純になりますが、学習データの全体的な特徴を捉えるようになります。最適なkの値は交差検証などの手法を使ってデータに基づいて選択するのが一般的です。

次に、Pythonでの簡単な実装例とグラフを示します。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

# データ生成
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2, random_state=42, n_clusters_per_class=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# k-NNモデルの訓練
k = 3
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
accuracy = knn.score(X_test, y_test)

# プロット
xx, yy = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100), np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, marker="o", edgecolors='k')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, marker="x", edgecolors='k')
plt.title(f"k-NN (k={k}), Accuracy: {accuracy:.2f}")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()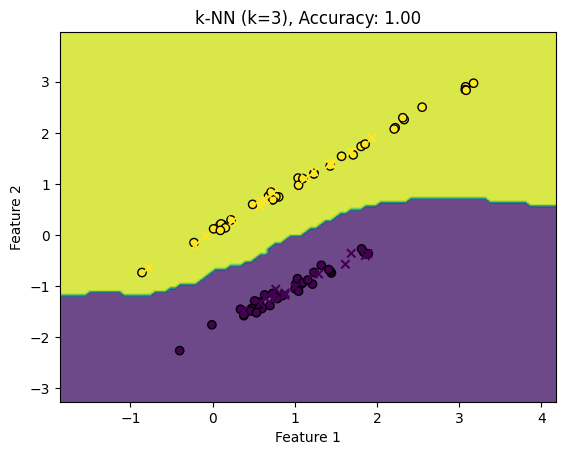

上のグラフは、k近傍法 アルゴリズムを使用して2つの特徴を持つデータを分類する例です。背景の色付き領域はk近傍法によって予測されたクラスを示しています。トレーニングデータは円で、テストデータは「x」で示されています。

このグラフを見ると、k=3のk近傍法 モデルがどのようにデータを分類するかが分かります。トレーニングデータの点が新しい点の「近傍」としてどのように機能するかを視覚的に理解するのに役立ちます。

この例からも、kの値やデータの分布によって、k近傍法の分類境界がどのように変わるかを観察できます。実際のアプリケーションでは、kの値を変えて交差検証することで、最適なkの値を見つけることが推奨されます。

距離尺度の選択

k近傍法やk平均法などのアルゴリズムでデータポイント間の「距離」を計算する際には、適切な距離尺度を選択することが重要です。以下は、一般的に用いられる3つの距離尺度についての説明です。

ユークリッド距離

ユークリッド距離は、私たちが普段考える「直線距離」と同じものです。2つの点 \( P(x_1, y_1) \) と \( Q(x_2, y_2) \) 間のユークリッド距離は次のように計算されます。

\[
d(P, Q) = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}
\]

この距離は、直感的で計算も簡単です。多次元空間でも拡張が可能です。

マンハッタン距離

マンハッタン距離（またはL1距離、シティブロック距離とも呼ばれる）は、2つの点間の距離を水平および垂直方向に移動することで計算します。数式で表すと以下のようになります。

\[
d(P, Q) = |x_2 – x_1| + |y_2 – y_1|
\]

この名前は、マンハッタンのグリッド状の通りを歩くことをイメージして名付けられました。

マハラノビス距離

マハラノビス距離は、データの変動や相関を考慮した距離尺度です。変数間の相関や分散が異なる場合に特に有用です。数式で表すと以下のようになります。

\[
d(P, Q) = \sqrt{(P – Q)^T \Sigma^{-1} (P – Q)}
\]

ここで、\( \Sigma \) はデータの共分散行列です。

次に、これらの距離尺度を用いて、Pythonで2つの点間の距離を計算する例を紹介します。

以下は、2つの点 \( P(2, 3) \) と \( Q(5, 7) \) 間の各距離尺度による計算結果です。

• ユークリッド距離: \( 5.0 \)
• マンハッタン距離: \( 7 \)
• マハラノビス距離: \( \approx 2.65 \) (仮の共分散行列を用いて計算)

これらの距離尺度は、データの特性やアプリケーションに応じて適切に選択する必要があります。ユークリッド距離やマンハッタン距離は計算が簡単で直感的ですが、データの変動や相関を考慮する場合、マハラノビス距離が適しています。

適切な距離尺度の選択は、アルゴリズムの性能を向上させます。

k近傍法の利点と欠点

k近傍法アルゴリズムは、その単純さと直感的な理解のしやすさからとって魅力的です。しかし、すべての機械学習アルゴリズムと同様に、k近傍法にもその利点と欠点があります。

利点:

1. 単純で直感的: k近傍法はとても単純なアルゴリズムであり、初心者にも理解しやすい。
2. トレーニングは高速: トレーニングデータを保存するだけなので、モデルのトレーニングに時間がかかりません。
3. 非線形の問題にも対応: k近傍法は非線形のデータにも対応できる。
4. パラメータが少ない: 最も重要なパラメータはkのみです。

欠点:

1. 予測が遅い: テストデータの各点に対してすべてのトレーニングデータとの距離を計算する必要があるため、予測に時間がかかります。
2. 高次元のデータ: 高次元のデータには「次元の呪い」が影響し、距離の計算がとても困難になる場合があります。
3. メモリ集約的: すべてのトレーニングデータをメモリに保存する必要があります。
4. kの選択: 適切なkの値を選ぶのは難しく、データによって最適な値が変わります。

k平均(k-means)法とは？

基本的な概念

k平均法は、非階層的なクラスタリングのアルゴリズムの1つで、データをk個のクラスタに分割することを目的としています。このアルゴリズムは、クラスタの重心を計算することで動作します。各データ点は最も近い重心に基づいてクラスタに割り当てられます。

アルゴリズムの流れ

1. 重心としてのk個のデータ点をランダムに選択します。
2. 各データ点を最も近い重心に基づいてクラスタに割り当てます。
3. 各クラスタの新しい重心を計算します。
4. 重心が変わらなくなるか、設定された繰り返し回数に達するまで、ステップ2と3を繰り返します。

次に、Pythonでのk平均の簡単な実装例とグラフを示します。

from sklearn.cluster import KMeans

# データ生成
X, _ = make_classification(n_samples=300, n_features=2, n_redundant=0, n_informative=2, random_state=42, n_clusters_per_class=1)

# k-meansモデルの訓練
k = 3
kmeans = KMeans(n_clusters=k, random_state=42)
y_kmeans = kmeans.fit_predict(X)

# プロット
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis', marker="o", edgecolors='k')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker="X", label="Centroids")
plt.title(f"k-means Clustering (k={k})")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.show()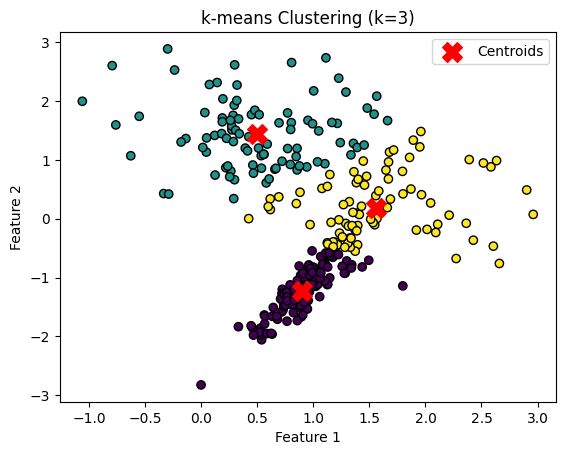

上のグラフは、k平均法アルゴリズムを使用して2つの特徴を持つデータをクラスタリングする例です。点の色はk平均法によって割り当てられたクラスタを示しており、赤い「X」マークは各クラスタの重心を示しています。

k平均法アルゴリズムは、データをk個のクラスタに分割することを目的としています。この例では、k=3のクラスタが形成され、それぞれのクラスタの重心が計算されています。

このグラフを通して、k平均法がどのようにデータをクラスタリングするか、そして各クラスタの中心がどのように計算されるかを視覚的に理解できます。特に、k平均法は「球状」のクラスタを仮定しているため、このような形状のデータセットに特に適しています。

kの選び方とその重要性

k平均法では、データをクラスタリングする際のクラスタ数 \( k \) の選択がとても重要です。適切な \( k \) の値を選ぶことで、データの構造やパターンをより正確に捉えることができます。しかし、\( k \) の最適な値は、一般的には事前に分かっているわけではありません。ここでは、クラスタ数 \( k \) の適切な値を選ぶための2つの一般的な手法、エルボー法とシルエット分析について説明します。

エルボー法

エルボー法は、さまざまな \( k \) の値に対するクラスタリングの品質を評価し、その結果をグラフにプロットすることで最適な \( k \) の値を視覚的に特定する方法です。この手法の名前は、グラフが「肘」のような形状を持つ点で最適な \( k \) が示されることに由来しています。

具体的には、クラスタ内の平方和（SSE）を計算し、それをさまざまな \( k \) の値に対してプロットします。最適な \( k \) の値は、SSEが急激に減少する「エルボー」と呼ばれる点として特定されます。

次に、Pythonでのエルボー法を用いた例を紹介します。

# エルボー法を用いて最適なkを見つける

# SSEを格納するリストを初期化
sse = []

# 試行するkのリスト
k_list = range(1, 11)

# 各kでk-meansを実行し、SSEを計算
for k in k_list:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    sse.append(kmeans.inertia_)

# エルボー法のグラフをプロット
plt.plot(k_list, sse, '-o')
plt.title("Elbow Method")
plt.xlabel("Number of clusters (k)")
plt.ylabel("SSE")
plt.xticks(k_list)
plt.grid(True)
plt.show()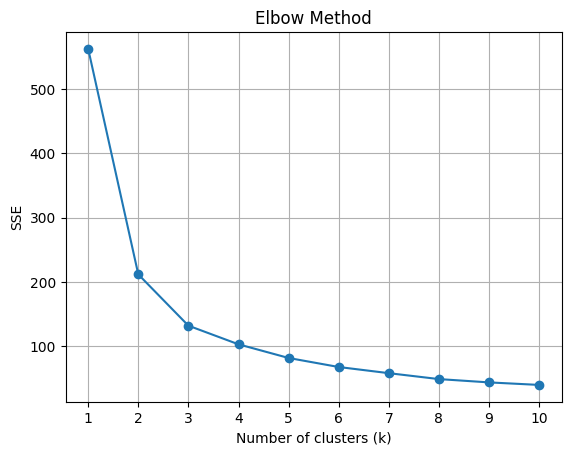

上のグラフはエルボー法を使用して、最適なクラスタ数 \( k \) を視覚的に特定する例です。クラスタ内の平方和（SSE）が急激に減少する点が「エルボー」として認識され、それが最適な \( k \) の値として提案されます。このデータセットの場合、\( k = 3 \) がエルボーとして認識される可能性が高いです。

シルエット分析

シルエット分析は、クラスタ内のサンプルがどれだけ密集しているかを定量的に評価する手法です。シルエット係数は、-1から1の範囲の値を取り、高い値はサンプルが適切なクラスタに属していることを示します。

シルエット係数は以下の式で計算されます:

\[
s(i) = \frac{b(i) – a(i)}{\max{a(i), b(i)}}
\]

ここで、\( a(i) \) はサンプル \( i \) と同じクラスタ内の他のすべてのサンプルとの平均距離、\( b(i) \) はサンプル \( i \) と最も近いクラスタのすべてのサンプルとの平均距離を表します。

次に、Pythonでのシルエット分析の例を紹介します。

from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
import numpy as np

# データ生成
X, _ = make_classification(n_samples=300, n_features=2, n_redundant=0, n_informative=2, random_state=42, n_clusters_per_class=1)

# シルエットスコアを格納するリストを初期化
silhouette_scores = []

# 試行するkのリスト（k=1の場合シルエットスコアは計算されないので、2から開始）
k_list_silhouette = range(2, 11)

# 各kでk-meansを実行し、シルエットスコアを計算
for k in k_list_silhouette:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    score = silhouette_score(X, kmeans.labels_)
    silhouette_scores.append(score)

# シルエットスコアのグラフをプロット
plt.plot(k_list_silhouette, silhouette_scores, '-o')
plt.title("Silhouette Analysis")
plt.xlabel("Number of clusters (k)")
plt.ylabel("Silhouette Score")
plt.xticks(k_list_silhouette)
plt.grid(True)
plt.show()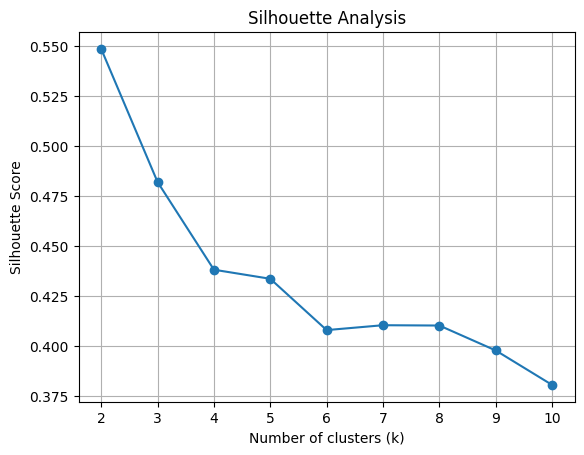

初期値の問題と解決策

k平均法アルゴリズムは、初期クラスタ中心の選択に敏感です。不適切な初期中心を選択すると、局所最適解に収束してしまう可能性があります。これは、最適なクラスタリングを得られない原因となり得ます。

k-means++

k-means++は、k-meansの初期中心をより賢明に選択する方法を提供します。以下は、k-means++の手順です。

1. 最初の中心をデータセットからランダムに選択します。
2. 2つ目以降の中心を選択する際に、すでに選択された中心からの距離に基づいて確率的にデータ点を選択します。具体的には、データポイントを選択する確率は、既存の中心からの距離の二乗に比例します。
3. k個の中心を選択するまで、ステップ2を繰り返します。
4. k平均法アルゴリズムを通常通り実行します。

k-means++の利用により、初期のクラスタ中心の選択が改善され、より良いクラスタリング結果を得る可能性が高まります。

k平均法の利点と欠点

利点：

1. 単純で理解しやすい: k平均法は、概念的に直感的であり、実装も比較的簡単です。
2. スケーラビリティ: 大量のデータに対しても比較的高速に動作します。
3. 広く利用されている: 多くの産業や研究分野で広く利用されています。

欠点：

1. 初期値の敏感さ: 不適切な初期中心の選択により、局所的最適解に収束するリスクがあります。
2. クラスタの数kを指定する必要がある: 最適なクラスタ数を知るための追加の技術や直感が必要です。
3. クラスタの形状: k平均法は、クラスタが円形または球形であると仮定します。そのため、異なる形状のクラスタを持つデータには適していない場合があります。
4. 外れ値の影響: k平均法は外れ値に敏感であり、クラスタリングの結果に大きな影響を与える可能性があります。

k平均法は多くのシチュエーションで役立ちますが、その特性と制約を理解し、適切に適用することが重要です。

k近傍法とk平均法の違い

目的と応用例

• k近傍法 (k-NN)
  • 目的: 未知のデータ点のクラスラベルを推定するために、最も近いトレーニングデータのラベルを利用します。
  • 応用例: 手書き数字の認識、映画の推薦、音楽のジャンル分類など、分類や回帰のタスクに使用されます。
• k平均法 (k-means)
  • 目的: データをk個のクラスタに分割し、データの構造やパターンを見つけ出します。
  • 応用例: 顧客セグメンテーション、文書クラスタリング、画像圧縮など、クラスタリングタスクに使用されます。

アルゴリズムの特性

• k近傍法
  • 教師あり学習アルゴリズム: トレーニングデータにラベルが必要です。
  • メモリベースの方法: トレーニングデータをすべて保存し、予測時に参照します。
  • 遅延学習: 学習フェーズが短く、ほとんどの計算は予測時に行われます。
• k平均法
  • 教師なし学習アルゴリズム: ラベルなしでデータの構造を見つけ出します。
  • 反復的な方法: クラスタ中心を更新するためにデータ上を何度も走査します。
  • リアルタイムの更新: 新しいデータが追加された際に、クラスタを更新できます。

計算コストと効率性

• k近傍法
  • 計算コスト: 大量のデータや高次元のデータになると、予測時の計算コストが高くなります。
  • 効率性: 高速な近傍検索アルゴリズムや次元削減手法を使用することで、効率性が向上します。
• k平均法
  • 計算コスト: クラスタの数や反復回数に応じて、計算コストが変わります。大量のデータに対しても比較的高速です。
  • 効率性: 初期値の選択やクラスタの数の選択により、効率性が変わります。k-means++やエルボー法などの技術を使用することで、効率性が向上します。

k近傍法とk平均法は、異なる目的と特性を持つアルゴリズムです。それぞれの問題やデータセットに応じて、適切なアルゴリズムを選択することが重要です。

実践！Pythonでの実装

k近傍法の実装例

k近傍法は、Pythonの機械学習ライブラリscikit-learnを使用して簡単に実装できます。以下は、簡単な例を紹介します。

# 必要なライブラリのインポート
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

# データのロード
data = load_iris()
X = data.data
y = data.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# k-NNモデルの作成と学習
k = 3
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)

# 予測と精度の計算
accuracy = knn.score(X_test, y_test)
print(f"Accuracy: {accuracy:.2f}")

Accuracy: 1.00

k平均法の実装例

k平均法もscikit-learnを使用して簡単に実装できます。

# 必要なライブラリのインポート
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# データの生成
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# k-meansモデルの作成とクラスタリング
k = 4
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)

# クラスタリングの結果をプロット
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red')
plt.title('K-means Clustering')
plt.show()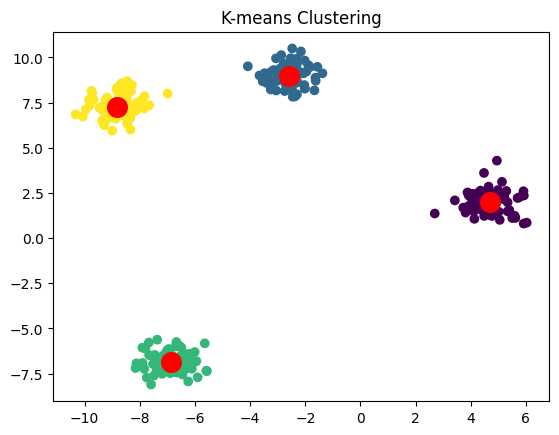

まとめ

k近傍法とk平均法のアルゴリズムは異なる目的と特性を持ち、適切な状況で使用することで、データ分析の多様な問題に対応できます。実際にPythonでの実装を通して、k近傍法とk平均法のアルゴリズムを理解し、実際のデータ分析に活用してください。

IT起業家

▼AIを使った副業・起業アイデアを紹介♪