目次
データサイエンティストの必須知識、「微分 | 数学の基礎」について解説します。
微分の基礎
はじめに
微分は、関数が小さな変化を受けたときのその変化の割合を表す数学の方法です。微分の概念は、物理学から経済学、生物学などのさまざまな分野で用いられています。特に、物の動きや変化の速さを知りたいときには、微分が欠かせません。
微分の基本的な考え方
- 定義:
微分とは、ある関数の任意の点における変化の割合を示すものです。数学的には、関数\( f(x) \)の点\( x \)における微分は以下のように表されます。 \[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) – f(x)}{h}
\] ここで、\( f'(x) \)は\( f(x) \)の導関数とも呼ばれ、\( x \)における傾きを示しています。 - 直感的な理解:
微分は、グラフのある点の傾きを示すものとして理解できます。たとえば、車の速度計はある瞬間の移動の速さを示しており、これは距離の関数に対する微分に相当します。
Pythonを使用して、基本的な関数の微分を可視化してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# Define a simple quadratic function and its derivative
def f(x):
return x**2
def df(x):
return 2*x
x = np.linspace(-10, 10, 400)
y = f(x)
dy = df(x)
plt.figure(figsize=(10,6))
plt.plot(x, y, label='f(x) = $x^2$', linewidth=2)
plt.plot(x, dy, label="f'(x) = 2x", linestyle='--', linewidth=2)
plt.title('Function and its Derivative')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()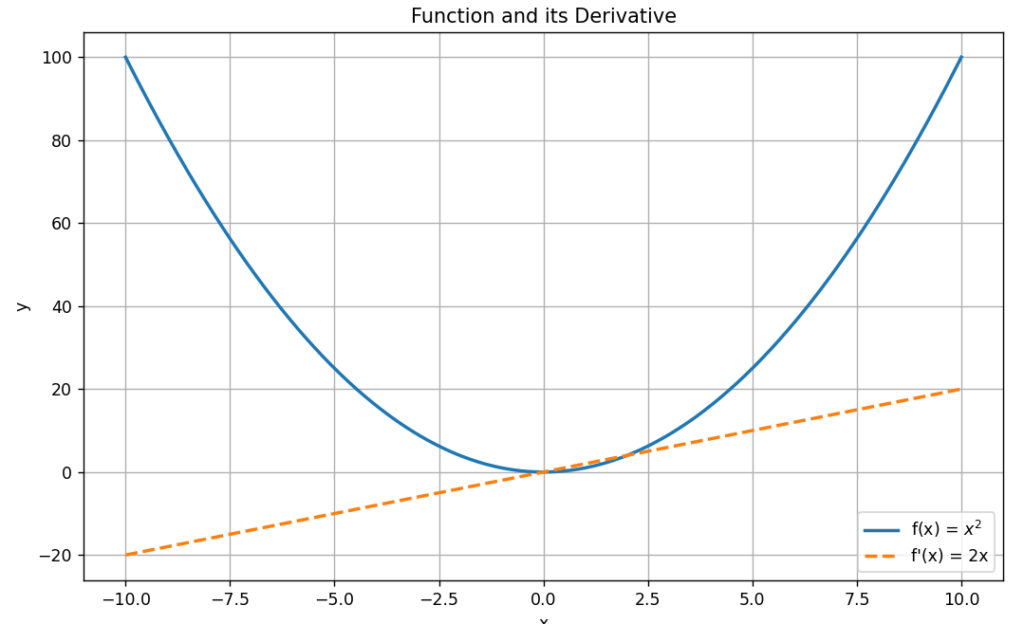
上のグラフでは、青い線が関数 \( f(x) = x^2 \) を、破線のオレンジの線がその導関数 \( f'(x) = 2x \) を示しています。関数 \( f(x) \) の形状から、その傾きがどのように変化するかを導関数を通して確認できます。
導関数 \( f'(x) \) の値は、元の関数 \( f(x) \) のある点での傾きを示しています。例えば、\( x = 2 \) の点での \( f(x) \) の傾きは \( f'(2) = 4 \) となります。
このように、微分を通じて関数の局所的な振る舞いや変化の速さを詳しく知ることができます。
微分の公式と性質
微分は、関数の形状や性質に応じて異なる公式や手法が存在します。ここでは、基本的な関数に関する微分の公式を紹介します。
- 多項式関数の微分:
多項式関数は、変数 \( x \) の整数べきで表される関数です。
例: \( f(x) = x^n \)
\[
\frac{d}{dx} x^n = nx^{n-1}
\]
この公式は、上述のグラフにも示されているものです。 - 三角関数の微分:
例: \( f(x) = \sin(x) \)
\[
\frac{d}{dx} \sin(x) = \cos(x)
\]
例: \( f(x) = \cos(x) \)
\[
\frac{d}{dx} \cos(x) = -\sin(x)
\] - 指数関数の微分:
例: \( f(x) = e^x \) (ネイピア数を底とする指数関数)
\[
\frac{d}{dx} e^x = e^x
\] - 対数関数の微分:
例: \( f(x) = \ln(x) \) (自然対数)
\[
\frac{d}{dx} \ln(x) = \frac{1}{x}
\]
これらの公式は、微分の計算においてとても頻繁に使用されます。特に多項式関数の微分公式は、他の多くの関数の微分を理解する基盤となります。
高階微分
関数を一度微分することを1階の微分と言いますが、さらにその結果を微分することで2階、3階と続けることができます。これを高階微分と呼びます。
- 2階微分:
\[
\frac{d^2}{dx^2} f(x)
\]
2階微分は、関数の「変化の変化」を示します。具体的には、関数の凹凸や変曲点を調べる際に用いられます。 - 3階微分:
\[
\frac{d^3}{dx^3} f(x)
\]
3階微分以降は、物理学や工学などの特定の分野での応用が考えられますが、日常的な問題解決にはあまり登場しません。
例として、先ほどの \( f(x) = x^2 \) を2階微分してみましょう。
\[
f”(x) = \frac{d^2}{dx^2} x^2
\]
この結果を計算してみます。
関数 \( f(x) = x^2 \) の2階微分は \( f”(x) = 2 \) となります。
これは、関数 \( f(x) = x^2 \) が全域で凸の形状をしていることを示しています。2階微分が正の場合、関数は凸(下に凹んでいる)であると言えます。
微分の公式と高階微分は関数の性質や形状を理解する上でとても役立つツールです。
連鎖律、積の微分、商の微分
微分は単一の関数だけでなく、複数の関数が組み合わさった形の関数にも適用できます。特に、関数の合成や積、商の形になった場合の微分方法はとても重要です。
- 連鎖律: 二つの関数の合成の微分は、外側の関数の微分と内側の関数の微分の積として表されます。
\[
\frac{d}{dx} f(g(x)) = f'(g(x)) \cdot g'(x)
\] - 積の微分: 二つの関数の積の微分は以下のようになります。
\[
\frac{d}{dx} [u(x) \cdot v(x)] = u'(x) \cdot v(x) + u(x) \cdot v'(x)
\] - 商の微分: 二つの関数の商の微分は以下のように表されます。
\[
\frac{d}{dx} \left[ \frac{u(x)}{v(x)} \right] = \frac{u'(x) \cdot v(x) – u(x) \cdot v'(x)}{[v(x)]^2}
\]
例題: 微分を用いた問題解決
- 曲線の接線の方程式を求める
問題: \(y = x^2 + 3x + 2\) の曲線上の点 \( (1,6) \) における接線の方程式を求めなさい。
解法:
まず、関数を微分します:
\[
\frac{d}{dx} (x^2 + 3x + 2) = 2x + 3
\]
次に、点 \( (1,6) \) での傾きを求めます:
\(2(1) + 3 = 5\)
最後に、点斜形式の方程式を用いて、接線の方程式を求めます:
\(y – 6 = 5(x – 1)\) - 関数の極大・極小の点を求める
問題: \(y = x^3 – 3x^2 + 2x\) の極大・極小の点を求めなさい。
解法:
関数を微分します:
\[
\frac{d}{dx} (x^3 – 3x^2 + 2x) = 3x^2 – 6x + 2
\]
得られた導関数を0と置いて、\(x\) の値を求めます。
\(3x^2 – 6x + 2 = 0\)
\(x\) の値を求めると、極大・極小の候補点が得られます。
それぞれの点における2階微分の値を計算して、極大・極小を判断します。
実際の応用例
微分は、ある瞬間の変化を捉える数学的ツールとして、多岐にわたる分野で活用されています。以下に、物理学と経済学における主な応用例を紹介します。
物理学: 運動の速度や加速度の計算
速度: 物体の位置を表す関数 \( s(t) \) が与えられたとき、その物体の速度 \( v(t) \) は位置関数の時間 \( t \) に関する導関数として表されます。
\[
v(t) = \frac{ds(t)}{dt}
\]
加速度: 速度関数 \( v(t) \) の導関数が加速度 \( a(t) \) となります。
\[
a(t) = \frac{dv(t)}{dt}
\]
例:
物体の位置を示す関数が \( s(t) = t^3 – 4t^2 + 2t \) で与えられたとき、速度と加速度を求めます。
\[ v(t) = \frac{ds(t)}{dt} \]
\[ a(t) = \frac{dv(t)}{dt} \]
経済学: 利益やコストの最大化問題
経済学において、企業が利益やコストを最大化(または最小化)するための最適な生産量や価格を決定する際に、微分は重要な役割を果たします。
利益関数の最大化:
利益関数 \( \pi(x) \) が与えられた場合、その最大値を求めるためには利益関数の導関数 \( \pi'(x) \) を0と置いて解きます。
例:
ある商品の利益関数が \( \pi(x) = -x^2 + 40x – 200 \) で与えられたとき、最大利益を得るための生産量 \( x \) を求めます。
\[ \pi'(x) = 0 \]
物理学における運動の解析や経済学における最適化問題など、微分は多岐にわたる分野での問題解決の鍵です。

▼AIを使った副業・起業アイデアを紹介♪
