Python, 高校数学, 統計学, 機械学習, ディープラーニングがなんと5時間で学べる！

データサイエンティストの必須知識、Python, 高校数学, 統計学, 機械学習, ディープラーニングを5時間で学びましょう！

Pythonの基礎

Pythonの基礎を学ぶために、まずは以下の概念を理解することが重要です。

変数 (Variables): 変数はデータを格納するための名前付きコンテナです。例えば、数値、テキスト、リスト、辞書などのデータを変数に格納できます。変数は後で再利用できます。

name = "John"  # 文字列をnameという変数に格納
age = 30       # 整数をageという変数に格納

データ型 (Data Types): Pythonはさまざまなデータ型をサポートしています。主要なデータ型には以下があります。

• 整数 (int): 正の整数や負の整数。例：5, -10
• 浮動小数点数 (float): 小数点を含む数値。例：3.14, 0.5
• 文字列 (string): テキストデータ。例："Hello, World!", 'Python'
• リスト (list): 複数の要素を順序付けて格納。例：[1, 2, 3], ["apple", "banana", "cherry"]
• 辞書 (dictionary): キーと値のペアを格納。例：{"name": "John", "age": 30}
• ブール (bool): 真 (True) または偽 (False) の値。条件式の結果として使用。例：True, False

変数への代入 (Variable Assignment): 変数に値を代入するには、変数名に対して等号 (=) を使用します。

x = 10  # xという変数に整数10を代入
name = "Alice"  # nameという変数に文字列"Alice"を代入

変数の使用 (Variable Usage): 代入された変数は後で使用できます。

print(x)  # 10 変数xの値を表示
print("Hello, " + name)  # Hello, Alice 文字列の結合

データ型の操作 (Data Type Operations): 各データ型は特定の操作をサポートします。例えば、数値の加算、文字列の結合、リストへの要素の追加などがあります。

num1 = 5
num2 = 3
result = num1 + num2  # 数値の加算
print(result)  # 8 結果を表示

greeting = "Hello, "
name = "Alice"
message = greeting + name  # 文字列の結合
print(message)  # Hello, Alice 結果を表示

fruits = ["apple", "banana"]
fruits.append("cherry")  # リストへの要素の追加
print(fruits)  # ['apple', 'banana', 'cherry'] 更新されたリストを表示

Pythonの基本的な概念である変数とデータ型を理解することは、プログラミングの基盤を築く重要なステップです。これらの概念を理解した後、条件分岐、ループ、関数などの高度なプログラミングトピックをマスターできます。

Pythonの基礎における条件分岐とループの使用について説明します。

条件分岐 (Conditional Statements):

条件分岐は、プログラムが特定の条件に応じて異なるアクションを実行するための制御構造です。Pythonでは主に以下の2つの条件分岐が使用されます。

if文 (if statement): 特定の条件が真 (True) の場合、指定されたコードブロックを実行します。

age = 20
if age >= 18:
    print("成人です。")

# 成人です。

if-else文 (if-else statement): 条件が真の場合と偽 (False) の場合、それぞれ異なるコードブロックを実行します。

age = 15
if age >= 18:
    print("成人です。")
else:
    print("未成年です。")

# 未成年です。

if-elif-else文 (if-elif-else statement): 複数の条件をチェックし、最初に真の条件に合致したブロックを実行します。最後のelse節はどの条件にも合致しない場合に実行されます。

score = 85
if score >= 90:
    print("優秀です。")
elif score >= 70:
    print("普通です。")
else:
    print("不合格です。")

# 普通です。

ループ (Loops):

ループは、同じコードブロックを繰り返し実行するための制御構造です。Pythonでは主に以下の2つのループが使用されます。

forループ (for loop): シーケンス（リスト、タプル、文字列など）内の要素を繰り返し処理します。

fruits = ["りんご", "バナナ", "いちご"]
for fruit in fruits:
    print(fruit)

# りんご
# バナナ
# いちご

whileループ (while loop): 指定した条件が真の間、繰り返し処理を続けます。

count = 0
while count < 5:
    print(count)
    count += 1

# 0
# 1
# 2
# 3
# 4

breakとcontinue: ループ内で使用され、breakはループを終了し、continueは現在の繰り返しをスキップして次の繰り返しに進みます。

for i in range(5):
    if i == 3:
        break  # iが3のときループ終了
    print(i)

for i in range(5):
    if i == 3:
        continue  # iが3のとき次のループへ
    print(i)


# 1
# 2
# 0
# 1
# 2
# 4

条件分岐とループは、プログラミングでさまざまなタスクを自動化し、データを処理するために不可欠な概念です。これらを使いこなすことで、複雑なプログラムを作成できるようになります。

Pythonの基礎における関数の定義と呼び出しについて説明します。

関数の定義 (Function Definition):

関数は、一連の処理をまとめて名前をつけ、再利用可能なブロックとして定義します。関数を定義することで、同じ処理を何度も記述せずに済み、コードのメンテナンスが容易になります。

Pythonでは関数を次のように定義します。

def greet(name):
    """指定された名前で挨拶する関数"""
    print(f"こんにちは、{name}さん！")

• def キーワードを使って関数を開始します。
• 関数名 (greet) は自分で決めることができます。
• 関数の引数（ここでは name）は、関数に渡す情報を指定します。
• 引数を取らない場合、() 内を空にします。
• 関数の本体はコロン (:) の後にインデントされています。
• 関数のドキュメンテーション文字列（""" """で囲まれた部分）は、関数の説明を提供します。

関数の呼び出し (Function Call):

関数を呼び出すことで、定義した関数の中に含まれる処理が実行されます。関数を呼び出すには、関数名に引数を渡します。

greet("Alice")

# こんにちは、Aliceさん！

• 関数名 (greet) を呼び出し、引数として "Alice" を渡しています。

戻り値 (Return Value):

関数はしばしば値を返すことがあります。これを戻り値と呼び、return ステートメントを使用して指定します。戻り値がある場合、関数の呼び出し元でその値を利用できます。

def add(a, b):
    """2つの数値を足し合わせる関数"""
    result = a + b
    return result

sum = add(3, 5)
print(sum)

# 8

• return ステートメントは関数内で計算された値を呼び出し元に返します。
• 戻り値を変数 (sum) に代入して利用できます。

関数はプログラムの構造化に役立ち、同じ処理を何度も書かずに済むため、コードの保守性と可読性を向上させます。関数をうまく活用することで、効率的なプログラミングが可能になります。

Pythonの基礎におけるモジュールのインポートと使用について説明します。

モジュールのインポート (Module Import):

Pythonでは、モジュールと呼ばれる外部のコードを利用できます。モジュールは、関数や変数を含んだPythonのスクリプトファイルです。モジュールを使用するためには、それをインポートする必要があります。

モジュールのインポートは次のように行います。

import モジュール名

例えば、Pythonの標準ライブラリであるmathモジュールをインポートする場合：

import math

モジュールの使用 (Module Usage):

モジュールをインポートすると、そのモジュール内で定義されている関数や変数を使用できるようになります。モジュールの要素を使用するには、モジュール名の後にドット (.) を付けてアクセスします。

例えば、mathモジュールのsqrt関数を使用して平方根を計算する場合：

import math

x = 25
y = math.sqrt(x)  # mathモジュール内のsqrt関数を使用して平方根を計算
print(y)  

# 5.0

モジュールの別名 (Module Alias):

モジュール名が長い場合や、同じ名前のモジュールが複数存在する場合、モジュールに別名（エイリアス）をつけることができます。これにより、短い名前でモジュールを使用できます。

別名をつけるには、asキーワードを使用します。

例えば、matplotlib.pyplotモジュールをpltとしてインポートする場合：

import matplotlib.pyplot as plt

特定の要素のみインポート (Import Specific Elements):

モジュールから特定の関数や変数のみをインポートすることもできます。これにより、モジュール全体をインポートする必要がなく、必要な要素のみを使えます。

例えば、randomモジュールからrandint関数だけをインポートする場合：

from random import randint

これにより、randint関数をrandom.randintではなく、単にrandintとして使用できます。

モジュールを使うことで、他の人が作成した便利なコードを再利用できるため、Pythonの強力な機能の一つです。プログラムを効率的に書くために、適切なモジュールを見つけて活用することが大切です。

Pythonの基礎におけるエラーハンドリングと例外処理について説明します。

エラーハンドリングとは (Error Handling):

プログラムを実行している際にエラーが発生することはよくあります。エラーが発生した場合、プログラムがクラッシュすることを避けるために、エラーをキャッチして適切に処理することが重要です。これをエラーハンドリングと呼びます。

例外とは (Exceptions):

Pythonでは、エラーは例外として扱われます。例外は予期せぬ状況やエラーを示すオブジェクトです。例外が発生すると、プログラムの実行が中断され、対応するエラーメッセージが表示されます。

例外処理の基本 (Basic Exception Handling):

Pythonではtryとexceptキーワードを使用して例外処理を実装します。基本的な構文は以下の通りです。

try:
    # 例外が発生する可能性のあるコード
except エラーの種類 as 変数:
    # エラーが発生した場合の処理

例えば、ゼロで割り算を試みるとZeroDivisionErrorという例外が発生します。この例外をキャッチして処理するコードは以下のようになります。

try:
    result = 10 / 0  # ゼロで割り算
except ZeroDivisionError as e:
    print("エラーが発生しました:", e)

複数の例外の処理 (Handling Multiple Exceptions):

複数の異なる種類の例外をキャッチすることも可能です。例外処理は上から順番に評価され、最初にマッチした例外が処理されます。

try:
    # 例外が発生する可能性のあるコード
except エラーの種類1 as 変数1:
    # エラー1が発生した場合の処理
except エラーの種類2 as 変数2:
    # エラー2が発生した場合の処理

例えば、ゼロで割り算と値の変換エラーを処理するコードは以下のようになります。

try:
    result = int("abc") / 0  # 値の変換エラーとゼロで割り算
except ValueError as e:
    print("値の変換エラーが発生しました:", e)
except ZeroDivisionError as e:
    print("ゼロで割り算のエラーが発生しました:", e)

例外処理の最後 (Finally Block):

tryとexceptの後にfinallyブロックを追加できます。finallyブロックは例外が発生してもしなくても、最終的に実行されるコードを含む場所です。たとえば、ファイルを閉じる操作などに使用されます。

try:
    # 例外が発生する可能性のあるコード
except エラーの種類 as 変数:
    # エラーが発生した場合の処理
finally:
    # 例外の有無にかかわらず実行される処理

例えば、ファイルを開いて処理し、必ずファイルを閉じるコードは次のようになります。

try:
    file = open("example.txt", "r")
    content = file.read()
except FileNotFoundError as e:
    print("ファイルが見つかりませんでした:", e)
finally:
    file.close()  # ファイルを閉じる

エラーハンドリングと例外処理を適切に行うことで、プログラムの信頼性を高め、エラーが発生してもプログラムがクラッシュしないようにできます。

NumPy（Numerical Python）は、Pythonで数値計算を行うための重要なライブラリです。以下にNumPyの基本的な使用法とインストール方法を説明します。

NumPyのインストール (Installation):

NumPyを使用するには、まずライブラリをインストールする必要があります。通常、次の方法でインストールできます。

pipを使用してインストール:

pip install numpy

Anacondaを使用してインストール（Anacondaを使用している場合）:

conda install numpy

NumPyのインポート (Importing NumPy):

NumPyをインストールしたら、Pythonプログラムで使用するために次のようにライブラリをインポートします。

import numpy as np

このようにすることで、NumPyの機能を使用できるようになります。npという別名（エイリアス）を使用することが一般的ですが、他の名前を選ぶこともできます。

NumPyの基本的な機能 (Basic NumPy Features):

NumPyは多次元配列（ndarray）を扱うための強力なツールを提供します。以下はNumPyの基本的な機能のいくつかです。

多次元配列の作成: NumPyの主要なデータ構造は多次元配列です。これらの配列を作成するには、np.array()関数を使用します。

arr = np.array([1, 2, 3, 4, 5])

配列の操作: 配列内の要素へのアクセス、スライシング、変更などができます。

print(arr[0])        # 要素へのアクセス
# 1

print(arr[1:4])      # スライス
# [2 3 4]

arr[2] = 10           # 要素の変更

配列の演算: NumPyを使用して、配列同士の演算（加算、減算、乗算、除算など）が簡単に行えます。

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
result = arr1 + arr2  # 配列同士の加算

多次元配列: NumPyでは多次元配列を簡単に作成できます。

matrix = np.array([[1, 2, 3], [4, 5, 6]])

統計処理: NumPyは配列内の統計的な計算（平均、合計、標準偏差など）をサポートします。

mean_value = np.mean(arr)
sum_value = np.sum(arr)

これらはNumPyの基本的な機能の一部です。NumPyはデータ処理、科学計算、機械学習などの幅広い分野で使用され、数値計算を効率的に行うための必須ツールとして広く使われています。NumPyの公式ドキュメントやチュートリアルを参照すると、さらに詳細な情報を得ることができます。

NumPyは、多次元配列（通常はndarrayと呼ばれる）を操作するためのPythonライブラリで、数値計算、データ処理、科学計算などに広く使用されます。以下では、NumPy配列の基本的な作成と操作について説明します。

NumPy配列（ndarray）の作成:

リストからNumPy配列を作成する:

import numpy as np

my_list = [1, 2, 3, 4, 5]
my_array = np.array(my_list)

これにより、PythonのリストからNumPy配列が作成されます。

ゼロ配列や一様な値の配列を作成する:

zeros_array = np.zeros(5)  # 0で初期化された長さ5の配列
ones_array = np.ones(3)   # 1で初期化された長さ3の配列
constant_array = np.full(4, 7)  # 7で初期化された長さ4の配列

範囲を持つ配列を作成する:

range_array = np.arange(1, 10, 2)  # 1から9までの奇数を持つ配列

ランダムな値を持つ配列を作成する:

random_array = np.random.rand(3, 3)  # 3x3のランダムな値を持つ配列

NumPy配列の操作:

要素へのアクセス:

my_array = np.array([1, 2, 3, 4, 5])
print(my_array[0])  # 1番目の要素にアクセス

# 1

スライシング:

sliced_array = my_array[1:4]  # インデックス1から3までの要素を取得

配列の演算:

array1 = np.array([1, 2, 3])
array2 = np.array([4, 5, 6])
result = array1 + array2  # 配列同士の加算

形状の変更:

original_array = np.array([1, 2, 3, 4, 5, 6])
reshaped_array = original_array.reshape(2, 3)  # 2x3の形状に変更

要素の追加と削除:

array = np.array([1, 2, 3])
new_array = np.append(array, 4)  # 要素を末尾に追加
removed_array = np.delete(array, 1)  # インデックス1の要素を削除

これらはNumPy配列の基本的な作成と操作の一部です。NumPyは、数値計算の高速化やデータ処理の効率化に役立つとても強力なライブラリです。NumPyを使いこなすことで、データの操作や解析が簡単に行えるようになります。

NumPyの配列（ndarray）では、要素にアクセスするためのインデックスとスライシングを使用します。以下では、これらの基本的な操作について説明します。

配列のインデックス:

NumPy配列の要素にアクセスするには、要素のインデックスを指定します。Pythonリストと同様に、インデックスは0から始まります。

import numpy as np

my_array = np.array([10, 20, 30, 40, 50])

# インデックスを使用して要素にアクセス
element = my_array[2]  # インデックス2の要素にアクセス (30)

配列のスライシング:

スライシングを使用すると、配列内の連続した要素のサブセットを取得できます。

import numpy as np

my_array = np.array([10, 20, 30, 40, 50])

# スライスを使用して要素のサブセットを取得
subset = my_array[1:4]  # インデックス1から3までの要素を取得 ([20, 30, 40])

スライスは、開始位置と終了位置（終了位置は含まれない）を指定します。上記の例では、インデックス1から3までの要素が取得されています。

ステップ値を指定したスライシング:

さらに、スライス時にステップ値を指定することもできます。ステップ値は、要素をどれだけスキップするかを制御します。

import numpy as np

my_array = np.array([10, 20, 30, 40, 50, 60, 70, 80])

# ステップ値を指定したスライス
subset = my_array[1:7:2]  # インデックス1から6までの要素を2つおきに取得 ([20, 40, 60])

この例では、インデックス1から6までの要素を2つおきに取得しています。

これらの操作を駆使することで、NumPy配列内の要素を効果的に操作し、データ処理や解析ができます。

NumPyを使った配列の数学的演算は、データ処理や科学計算においてとても重要です。以下に、NumPyを使用して配列を使った基本的な数学的演算について説明します。

配列同士の基本的な演算:

加算と減算:
NumPyの配列同士を加算または減算できます。配列の要素ごとに演算が行われます。

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])

# 配列の加算
result_add = arr1 + arr2  # [5, 7, 9]

# 配列の減算
result_subtract = arr1 - arr2  # [-3, -3, -3]

乗算と除算:
同様に、NumPyの配列同士を乗算または除算することもできます。

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])

# 配列の乗算
result_multiply = arr1 * arr2  # [4, 10, 18]

# 配列の除算
result_divide = arr1 / arr2  # [0.25, 0.4, 0.5]

配列の数学的演算関数:

NumPyには、配列に対して数学的な操作を行うための関数も用意されています。

内積:
配列同士の内積は np.dot() 関数を使用して計算できます。

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])

# 配列の内積
result_dot = np.dot(arr1, arr2)  # 32

平方根や三角関数:
NumPyは、np.sqrt()（平方根）、np.sin()（正弦）、np.cos()（余弦）、np.tan()（正接）など、多くの数学関数も提供しています。

import numpy as np

arr = np.array([1, 4, 9])

# 平方根の計算
result_sqrt = np.sqrt(arr)  # [1. 2. 3.]

# 正弦の計算
result_sin = np.sin(arr)  # [0.84147098 -0.7568025 0.41211849]

これらの基本的な数学的演算は、NumPyの強力な機能を活用して、さまざまな数値計算やデータ処理のタスクで使用できます。

NumPyを使用した配列の統計的操作は、データ解析や科学計算においてとても重要です。以下に、NumPyを使って配列の統計的操作を行う方法を説明します。

配列の統計的操作:

平均値（平均）の計算:
NumPyの np.mean() 関数を使用して、配列の平均値を計算できます。

import numpy as np

arr = np.array([1, 2, 3, 4, 5])

# 平均値の計算
mean_value = np.mean(arr)  # 3.0

中央値の計算:
中央値は、データの中央に位置する値を示します。NumPyの np.median() 関数を使用して中央値を計算できます。

import numpy as np

arr = np.array([1, 2, 3, 4, 5])

# 中央値の計算
median_value = np.median(arr)  # 3.0

分散と標準偏差の計算:
分散と標準偏差は、データのばらつき度合いを示す統計的な指標です。分散は np.var()、標準偏差は np.std() 関数を使用して計算できます。

import numpy as np

arr = np.array([1, 2, 3, 4, 5])

# 分散の計算
variance_value = np.var(arr)  # 2.5

# 標準偏差の計算
std_deviation_value = np.std(arr)  # 1.5811388300841898

最大値と最小値の取得:
最大値と最小値は、データの範囲を示す指標です。np.max() と np.min() 関数を使用して取得できます。

import numpy as np

arr = np.array([1, 2, 3, 4, 5])

# 最大値の取得
max_value = np.max(arr)  # 5

# 最小値の取得
min_value = np.min(arr)  # 1

これらの統計的操作は、NumPyを使用して配列データの特性を理解し、データ解析や科学的な研究に活用する際に役立ちます。

NumPyのブロードキャストは、異なる形状の配列間で演算を行う際に、自動的に形状を調整して計算を行う機能です。これにより、形状の異なる配列間で要素ごとの演算を簡単に行うことができます。以下に、NumPyのブロードキャストの基本的な考え方を説明します。

ブロードキャストの基本:

1. 形状の一致:
   ブロードキャストを行うためには、少なくとも片方の配列の形状が他方の配列の形状に対して「適合」している必要があります。形状の一致とは、次元ごとに対応する次元のサイズが等しいことを意味します。例えば、1次元配列と2次元配列をブロードキャストする場合、1次元の配列を2次元に「拡張」することが考えられます。
2. 自動拡張:
   ブロードキャストにおいて、NumPyは自動的に形状を調整して計算を実行します。形状の不一致がある場合、NumPyは適切に拡張して演算を行います。

ブロードキャストの例:

import numpy as np

# 1次元配列とスカラーの演算 (スカラーが1次元に拡張される)
arr1 = np.array([1, 2, 3, 4])
result = arr1 + 2  # [3, 4, 5, 6]

# 2次元配列と1次元配列の演算 (1次元配列が2次元に拡張される)
arr2 = np.array([[1, 2], [3, 4]])
arr3 = np.array([10, 20])
result = arr2 + arr3
# 結果:
# [[11 22]
#  [13 24]]

上記の例では、ブロードキャストによってスカラーと1次元配列、または1次元配列と2次元配列の間で演算が実行されました。NumPyは、配列を必要な形状に拡張して計算を行っています。

ブロードキャストは、NumPyを使って効率的なコードを書く上でとても便利であり、ループを明示的に書かずに多くの要素ごとの操作を実現します。

Matplotlibは、Pythonでグラフやプロットを作成するためのとても人気のあるライブラリです。Matplotlibを使ってグラフを描画するためには、まずMatplotlibをインストールし、必要なライブラリをインポートする必要があります。以下に、Matplotlibの基本的な使い方を説明します。

Matplotlibのインストールとインポート:

Matplotlibを使うためには、まずインストールが必要です。通常、次のコマンドを使用してMatplotlibをインストールできます。

pip install matplotlib

インストールが完了したら、Pythonスクリプト内でMatplotlibをインポートします。

import matplotlib.pyplot as plt

ここで、pltは一般的な別名で、Matplotlibの関数やメソッドを使う際に便利です。この別名は慣習的によく使用されますが、別の名前を選んでも問題ありません。

グラフの描画:

Matplotlibを使ってグラフを描画する際には、以下のステップに従います。

1. データの準備: グラフに表示するデータを用意します。
2. グラフの作成: plt.figure()を使用して新しいグラフを作成します。
3. プロット: データをグラフにプロットします。例えば、plt.plot()を使用して線グラフを描画できます。
4. グラフのカスタマイズ: タイトル、軸ラベル、凡例などのカスタマイズを行います。
5. 表示または保存: plt.show()を使用してグラフを表示するか、plt.savefig()を使用して画像ファイルとして保存します。

以下は、Matplotlibを使用して簡単な折れ線グラフを描画する例です。

import matplotlib.pyplot as plt

# データの準備
x = [1, 2, 3, 4, 5]
y = [10, 12, 5, 8, 14]

# グラフの作成
plt.figure()

# プロット
plt.plot(x, y)

# グラフのカスタマイズ
plt.title('Line graph example')
plt.xlabel('X')
plt.ylabel('Y')

# グラフの表示
plt.show()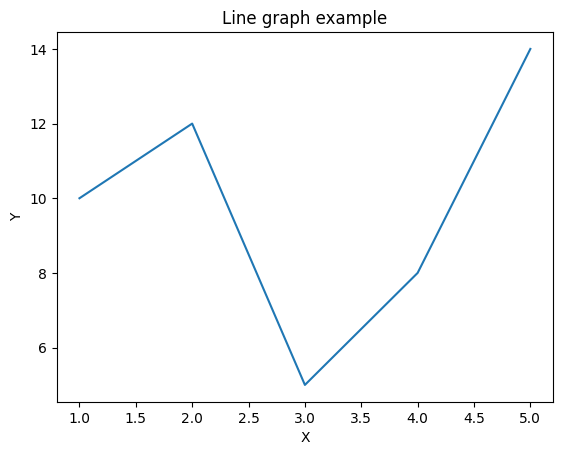

このコードは、Matplotlibを使って単純な折れ線グラフを描画する例です。必要に応じて、さまざまな種類のグラフを描画したり、カスタマイズしたりできます。 Matplotlibの公式ドキュメンテーションにはさらに詳細な情報が提供されています。

Matplotlibを使用して折れ線グラフを描画するためには、以下のステップに従います。

データを用意する: グラフに表示したいデータをPythonのリストやNumPy配列などで用意します。

Matplotlibをインポートする: MatplotlibライブラリをPythonスクリプトにインポートします。

import matplotlib.pyplot as plt

データをプロットする: plt.plot()関数を使用してデータをプロットします。この関数にX軸とY軸のデータを渡します。

x = [1, 2, 3, 4, 5]  # X軸のデータ
y = [10, 12, 5, 8, 14]  # Y軸のデータ
plt.plot(x, y)  # プロット

グラフのカスタマイズ: グラフの見た目をカスタマイズできます。タイトル、軸ラベル、凡例、線のスタイル、色などを設定できます。

plt.title('Line graph example')  # グラフのタイトル
plt.xlabel('X')  # X軸のラベル
plt.ylabel('Y')  # Y軸のラベル
plt.legend(['データ'])  # 凡例
plt.grid(True)  # グリッド線の表示

グラフの表示または保存: plt.show()関数を使用してグラフを表示します。または、plt.savefig()関数を使用して画像ファイルとして保存できます。

plt.show()  # グラフを表示
# plt.savefig('my_plot.png')  # グラフを画像ファイルとして保存（オプション）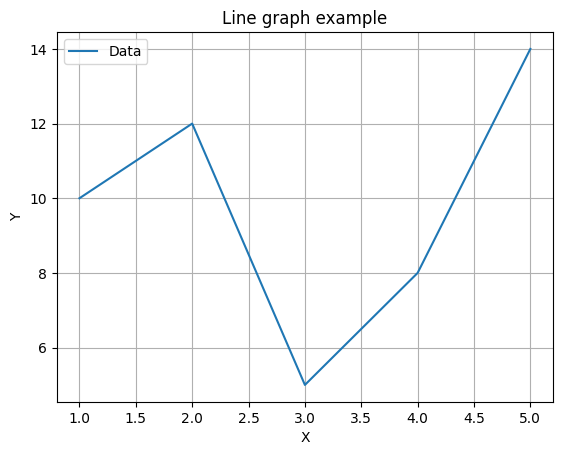

以下は、これらのステップを組み合わせた折れ線グラフの例です。

import matplotlib.pyplot as plt

# データの用意
x = [1, 2, 3, 4, 5]
y = [10, 12, 5, 8, 14]

# グラフの作成とプロット
plt.plot(x, y)

# グラフのカスタマイズ
plt.title('Line graph example')
plt.xlabel('X')
plt.ylabel('Y')

# グラフの表示
plt.show()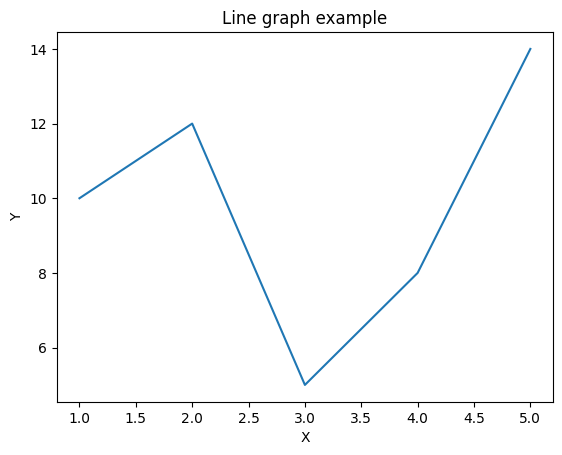

このコードを実行すると、指定したデータに基づいた折れ線グラフが表示されます。必要に応じて、データやグラフのカスタマイズを調整できます。

Matplotlibを使用して散布図（scatter plot）を描画するためには、以下のステップに従います。

データを用意する: グラフに表示したいデータをPythonのリストやNumPy配列などで用意します。データはX軸とY軸の値のペアとして持っておく必要があります。

Matplotlibをインポートする: MatplotlibライブラリをPythonスクリプトにインポートします。

import matplotlib.pyplot as plt

散布図をプロットする: plt.scatter()関数を使用して散布図をプロットします。この関数にX軸とY軸のデータを渡します。

x = [1, 2, 3, 4, 5]  # X軸のデータ
y = [10, 12, 5, 8, 14]  # Y軸のデータ
plt.scatter(x, y)  # 散布図のプロット

グラフのカスタマイズ: グラフの見た目をカスタマイズできます。タイトル、軸ラベル、凡例、点のサイズ、色などを設定できます。

plt.title('Example of Scatter Plot')  # グラフのタイトル
plt.xlabel('X')  # X軸のラベル
plt.ylabel('Y')  # Y軸のラベル
plt.legend(['Data'])  # 凡例
plt.grid(True)  # グリッド線の表示

グラフの表示または保存: plt.show()関数を使用してグラフを表示します。または、plt.savefig()関数を使用して画像ファイルとして保存できます。

plt.show()  # グラフを表示
# plt.savefig('my_scatter_plot.png')  # グラフを画像ファイルとして保存（オプション）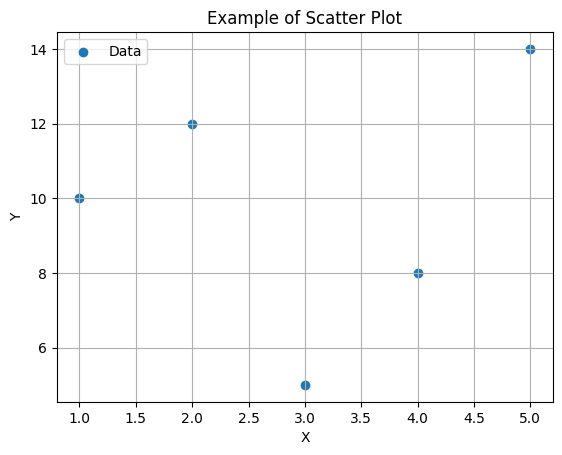

以下は、これらのステップを組み合わせた散布図の例です。

import matplotlib.pyplot as plt

# データの用意
x = [1, 2, 3, 4, 5]
y = [10, 12, 5, 8, 14]

# 散布図の作成とプロット
plt.scatter(x, y)

# グラフのカスタマイズ
plt.title('Example of Scatter Plot')  # グラフのタイトル
plt.xlabel('X')  # X軸のラベル
plt.ylabel('Y')  # Y軸のラベル

# グラフの表示
plt.show()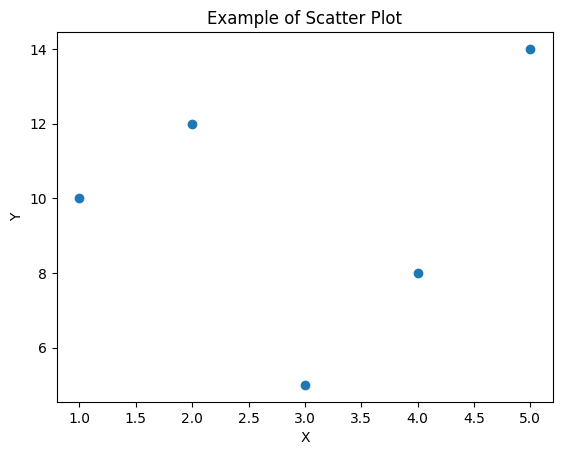

このコードを実行すると、指定したデータに基づいた散布図が表示されます。必要に応じて、データやグラフのカスタマイズを調整できます。

Matplotlibを使用してヒストグラムを作成するためには、以下のステップに従います。

データを用意する: ヒストグラムを作成したいデータをPythonのリストやNumPy配列などで用意します。

Matplotlibをインポートする: MatplotlibライブラリをPythonスクリプトにインポートします。

import matplotlib.pyplot as plt

ヒストグラムをプロットする: plt.hist()関数を使用してヒストグラムをプロットします。この関数にデータとビン（階級）の数を渡します。

data = [1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5]
plt.hist(data, bins=5)  # ヒストグラムのプロット

グラフのカスタマイズ: グラフの見た目をカスタマイズできます。タイトル、軸ラベル、凡例、ビンの幅、色などを設定できます。

import matplotlib.pyplot as plt

data = [1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5]
plt.hist(data, bins=5)  # ヒストグラムのプロット

plt.title('Histogram example')  # グラフのタイトル
plt.xlabel('Value')  # X軸のラベル
plt.ylabel('Frequency')  # Y軸のラベル
plt.grid(True)  # グリッド線の表示

グラフの表示または保存: plt.show()関数を使用してグラフを表示します。または、plt.savefig()関数を使用して画像ファイルとして保存できます。

plt.show()  # グラフを表示
# plt.savefig('my_histogram.png')  # グラフを画像ファイルとして保存（オプション）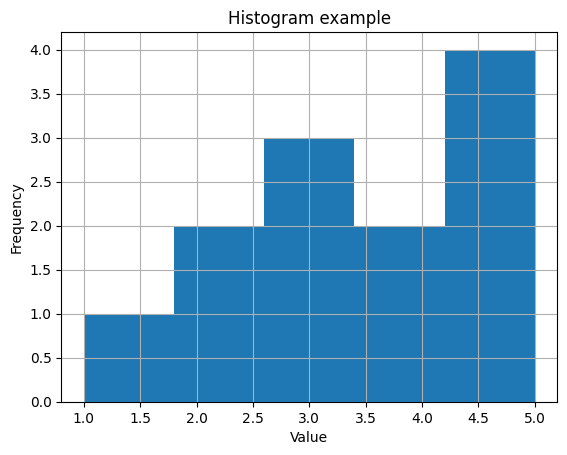

以下は、これらのステップを組み合わせたヒストグラムの例です。

import matplotlib.pyplot as plt

# データの用意
data = [1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5]

# ヒストグラムの作成とプロット
plt.hist(data, bins=5)

# グラフのカスタマイズ
plt.title('Histogram example')  # グラフのタイトル
plt.xlabel('Value')  # X軸のラベル
plt.ylabel('Frequency')  # Y軸のラベル

# グラフの表示
plt.show()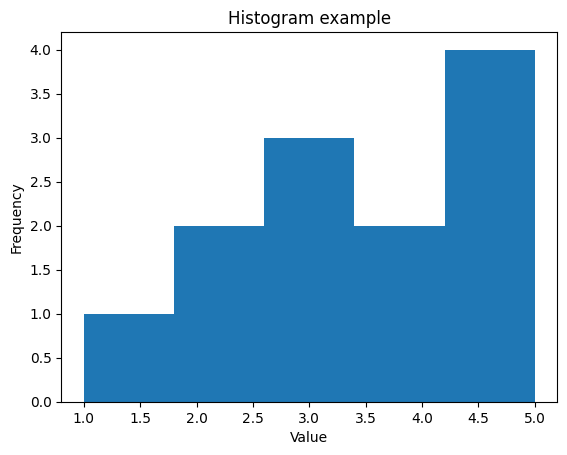

このコードを実行すると、指定したデータからヒストグラムが生成され、グラフが表示されます。必要に応じて、データやグラフのカスタマイズを調整できます。

Matplotlibを使用して棒グラフ（バーチャート）を作成するためには、以下のステップに従います。

データを用意する: 棒グラフを作成したいカテゴリや項目のデータを用意します。データはリストやNumPy配列などで表現されます。

Matplotlibをインポートする: MatplotlibライブラリをPythonスクリプトにインポートします。

import matplotlib.pyplot as plt

棒グラフをプロットする: plt.bar()関数を使用して棒グラフをプロットします。この関数にデータとX軸の位置を指定します。

categories = ['A', 'B', 'C', 'D', 'E']  # カテゴリや項目のリスト
values = [10, 15, 7, 12, 9]  # 各カテゴリの値
plt.bar(categories, values)  # 棒グラフのプロット

グラフのカスタマイズ: グラフの見た目をカスタマイズできます。タイトル、軸ラベル、凡例、色、幅などを設定できます。

plt.title('Bar chart example')  # グラフのタイトル
plt.xlabel('Category')  # X軸のラベル
plt.ylabel('Value')  # Y軸のラベル
plt.grid(axis='y', linestyle='--', alpha=0.7)  # Y軸にグリッド線を表示

グラフの表示または保存: plt.show()関数を使用してグラフを表示します。または、plt.savefig()関数を使用して画像ファイルとして保存できます。

plt.show()  # グラフを表示
# plt.savefig('my_bar_chart.png')  # グラフを画像ファイルとして保存（オプション）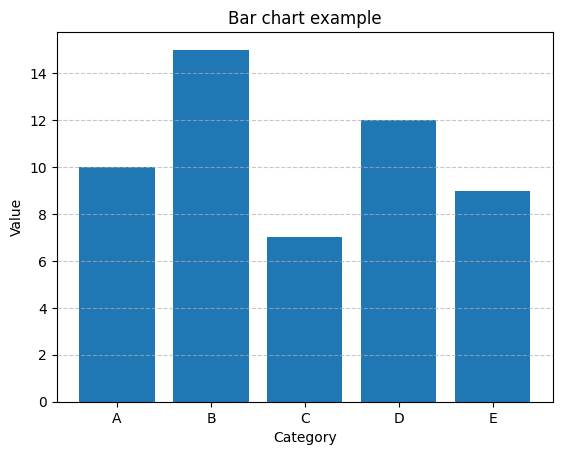

以下は、これらのステップを組み合わせた棒グラフの例です。

import matplotlib.pyplot as plt

# カテゴリと値のデータ
categories = ['A', 'B', 'C', 'D', 'E']
values = [10, 15, 7, 12, 9]

# 棒グラフの作成とプロット
plt.bar(categories, values)

# グラフのカスタマイズ
plt.title('Bar chart example')  # グラフのタイトル
plt.xlabel('Category')  # X軸のラベル
plt.ylabel('Value')  # Y軸のラベル

# グラフの表示
plt.show()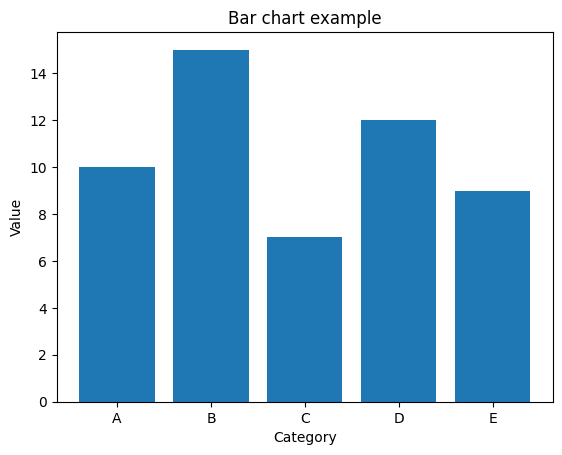

このコードを実行すると、指定したカテゴリと値から棒グラフが生成され、グラフが表示されます。必要に応じて、データやグラフのカスタマイズを調整できます。

Matplotlibを使用してグラフにラベル、タイトル、凡例を追加する方法を説明します。以下の例では、折れ線グラフを使いますが、同様の方法で他の種類のグラフにも適用できます。

ラベルの追加:

ラベルは、軸に対してデータの説明や単位を提供します。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [10, 15, 7, 12, 9]

plt.plot(x, y)
plt.xlabel('X_Label')
plt.ylabel('Y_Label')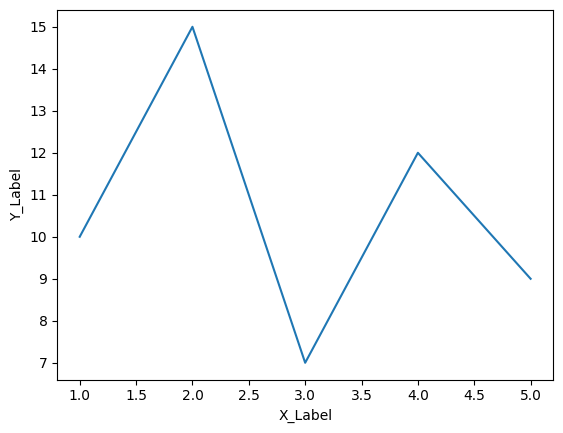

上記の例では、X軸とY軸に対するラベルが追加されました。

タイトルの追加:

グラフ全体に対するタイトルを追加できます。

plt.title('Graph Title')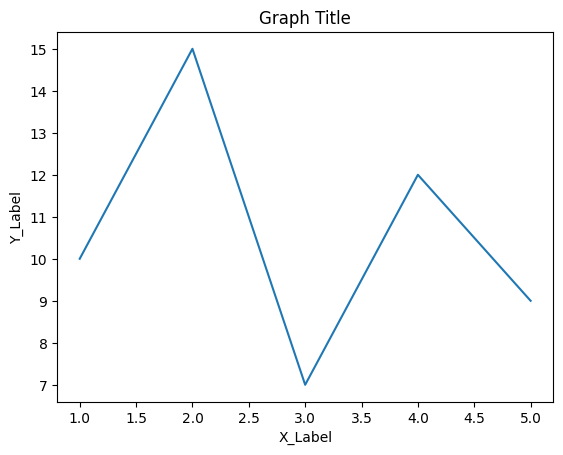

グラフのタイトルは、plt.title()関数を使用して指定します。

凡例の追加:

複数のデータセットがある場合、凡例はそれらのデータセットを区別するのに役立ちます。

plt.plot(x, y, label='データセット1')
plt.plot(x, [5, 8, 6, 9, 11], label='データセット2')
plt.legend()

labelパラメータを使用して各データセットに名前を付け、plt.legend()関数で凡例を表示します。凡例は各データセットの名前を示し、グラフのどこに表示するかはMatplotlibによって自動的に決定されます。

以下はこれらのステップを組み合わせた例です。

import matplotlib.pyplot as plt

plt.plot(x, y, label='Data Set 1')
plt.plot(x, [5, 8, 6, 9, 11], label='Data Set 2')
plt.legend()

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [10, 15, 7, 12, 9]

plt.plot(x, y, label='Data Set 1')
plt.xlabel('X_Label')
plt.ylabel('Y_Label')
plt.title('Graph Title')

# もう一つのデータセット
plt.plot(x, [5, 8, 6, 9, 11], label='Data Set 2')

# 凡例を表示
plt.legend()

plt.show()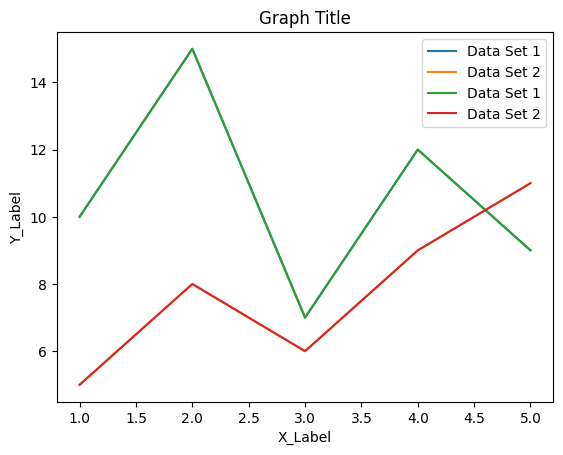

このコードを実行すると、折れ線グラフにX軸ラベル、Y軸ラベル、タイトル、凡例が追加されたグラフが表示されます。

Matplotlibを使用して作成したグラフを保存する方法を説明します。グラフを保存することは、後で再利用するため、報告書やプレゼンテーションに使用するために重要です。

Matplotlibでは、savefig()関数を使用してグラフをファイルに保存します。以下は、グラフを保存する手順です。

グラフを描画します。 まず、Matplotlibを使用してグラフを作成します。これは前の説明で説明した通りです。例えば、次のコードで折れ線グラフを描画します。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [10, 15, 7, 12, 9]

plt.plot(x, y)
plt.xlabel('X_Label')
plt.ylabel('Y_Label')
plt.title('Graph Title')

グラフをファイルに保存します。

savefig()関数を使用して、グラフを指定したファイル形式（通常はPNG、JPEG、PDFなど）で保存します。関数の第一引数にはファイル名を指定します。ファイル名には拡張子を含めることが重要です。

plt.savefig('グラフの保存先ファイル名.png')

このコードを実行すると、現在のディレクトリに指定したファイル名でグラフが保存されます。例えば、’グラフの保存先ファイル名.png’という名前のPNGファイルが作成されます。

以下は完全な例です。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [10, 15, 7, 12, 9]

plt.plot(x, y)
plt.xlabel('X_Label')
plt.ylabel('Y_Label')
plt.title('Graph Title')

# グラフをPNGファイルとして保存
plt.savefig('my_graph.png')

plt.show()

この例では、’my_graph.png’という名前のPNGファイルにグラフが保存されます。自分の用途に合わせてファイル名と保存形式を変更してください。

高校数学

位取り記数法

位取り記数法は、数を表現する方法の一つで、各桁が基数（通常は10進数または2進数）の累乗を表します。最も一般的な位取り記数法は10進法で、数字は0から9の範囲の記号で表されます。例えば、10進法での数「123」は、百の位（1）、十の位（2）、一の位（3）に分解されます。各位の値は、その位が基数の何乗であるかを示しています。

コンピュータでは、主に2進法が使用されます。2進法では、各桁が0または1の2つの値を取ります。例えば、2進法での数「1010」は、2の3乗（8）と2の1乗（2）を表します。これにより、コンピュータは電子回路のオンとオフ、またはビットの0と1で情報を表現します。

ビジネスの応用例

ビジネスの応用例としては、データベース内の大きな数字を効率的に格納するために、特定の基数に変換することがあります。たとえば、金融業界ではとても大きな金額や精密な計算を行う際に、位取り記数法を使用してデータを効率的に処理します。

Pythonコード

decimal_number = 1234
# 10進数を2進数に変換
binary_representation = bin(decimal_number)
print(f"10進数 {decimal_number} は2進数で {binary_representation} です。")

10進数 1234 は2進数で 0b10011010010 です。

基数変換

基数変換は、ある基数（進法）で表されている数を別の基数で表すプロセスです。通常、私たちは10進数を使用して数を表現しますが、コンピュータや特定のアプリケーションでは異なる基数が使用されることがあります。基数変換を行うことで、数を異なる基数で表現し直すことができます。

例えば、10進数の数を2進数や16進数に変換できます。2進数では0と1の2つの数字を使用し、16進数では0から9までの数字とAからFまでのアルファベットを使用します。これにより、同じ数を異なる基数で表現できます。

ビジネスの応用例

ビジネスの応用例としては、ハードウェア設計や低レベルのプログラミングで、データを異なる基数で処理する必要がある場合があります。また、ネットワークアドレスや色の表現など、特定のアプリケーションで異なる基数が使用されることもあります。

Pythonコード

decimal_number = 255
# 10進数を16進数に変換
hex_representation = hex(decimal_number)
print(f"10進数 {decimal_number} は16進数で {hex_representation} です。")

10進数 255 は16進数で 0xff です。

上記のPythonコードでは、10進数の数を16進数に変換しています。decimal_number変数に格納された10進数の数255は、hex()関数を使用して16進数に変換され、hex_representation変数に格納されます。その結果、10進数255は16進数で0xffと表されます。

2の補数と基数変換

2の補数は、負の整数を2進数で表現する方法です。この表現方法では、最も左のビット（最上位ビット）が符号ビットとして使用され、0は正の数を示し、1は負の数を示します。

たとえば、8ビットの2進数表現を考えてみましょう。通常、この場合、最も左のビットは符号ビットであり、0は正の数、1は負の数を示します。

• 正の整数3を2進数で表すと：00000011
• 負の整数-3を2の補数で表すと：11111101

2の補数を使用することで、正と負の数を同じ2進数表現で扱うことができます。この方法は、コンピュータ内で整数を表現する際に広く使用されています。また、2の補数を使用することで、加算と減算の操作が同じ回路で行えるため、コンピュータのハードウェア設計にも適しています。

ビジネスの応用例

コンピュータの算術演算で負の数を効率的に取り扱うために使用されます。

Pythonコード

def twos_complement(value, bits):
    if value < 0:
        value = (1 << bits) + value
    return format(value, f'0{bits}b')
# 例: -5の8ビット2の補数を計算し、2進数表現に変換
result = twos_complement(-5, 8)
print(result)

11111011

このコードでは、twos_complement 関数が2の補数を計算し、指定されたビット数の2進数表現に変換します。関数に負の値とビット数を渡すことで、負の値の2の補数を計算し、2進数文字列として返します。

実数を基数変換する

実数を基数変換するとは、実数を別の基数（通常は10進数から異なる基数）で表現することを意味します。このプロセスは、整数部と小数部を別々に変換し、それらを組み合わせて新しい基数の実数を得る方法です。

例えば、10進数から2進数への基数変換を考えてみましょう。整数部と小数部をそれぞれ2進数に変換し、最終的に結合します。

例：

• 整数部の10進数「12」を2進数に変換すると「1100」になります。
• 小数部の10進数「0.75」を2進数に変換すると「0.11」になります。

これらを組み合わせて、新しい基数（2進数）での実数「1100.11」が得られます。

ビジネスの応用例

ビジネスの応用例としては、特定の計算処理で異なる基数のデータを取り扱う必要がある場合があります。たとえば、コンピュータの内部処理では2進数が使用され、ネットワーク通信やデータ圧縮などのアプリケーションでは16進数が使用されることがあります。基数変換は、これらの異なる基数のデータを相互に変換するために使用されます。

Pythonコード

def float_to_binary(value, places=8):
    integral_part = int(value)
    fractional_part = value - integral_part
    # 整数部の変換
    integral_binary = bin(integral_part).split("b")[1]
    fractional_binary = []
    while places:
        fractional_part *= 2
        bit = int(fractional_part)
        fractional_part -= bit
        fractional_binary.append(str(bit))
        places -= 1
    return integral_binary + "." + "".join(fractional_binary)
# 例: 10.625の2進数表現（8ビット精度）
result = float_to_binary(10.625, places=8)
print(result)

1010.10100000

このコードでは、与えられた実数を整数部と小数部に分割し、それぞれを2進数に変換してから合成します。整数部は bin() 関数を使用して2進数文字列に変換し、小数部は指定された精度（ビット数）まで2進数に変換します。最終的に、整数部と小数部を連結して実数の2進数表現を得ることができます。

シフト演算で掛け算・割り算

シフト演算は、2進数での数値を左にシフト（左シフト）または右にシフト（右シフト）する操作です。これらの演算は、掛け算や割り算に相当します。

• 左シフト（<<）: 左シフト演算は、数値を左に指定したビット数だけシフトします。これは、数値を2の累乗で掛ける操作として理解できます。例えば、4を2で左シフトすると、4 * 2^2 = 16 になります。
• 右シフト（>>）: 右シフト演算は、数値を右に指定したビット数だけシフトします。これは、数値を2の累乗で割る操作として理解できます。例えば、4を2で右シフトすると、4 / 2^2 = 1 になります。

ビジネスの応用例

シフト演算は、高速な計算が必要なアプリケーションやリアルタイムシステムでの計算処理の最適化に使用されます。

1. 組み込みシステム: 組み込みシステムやマイクロコントローラでは、リソースが限られているため、効率的な計算が必要です。シフト演算は、リソース制約のある環境での計算を高速化します。
2. データ圧縮: データ圧縮アルゴリズム（例: ハフマン符号化）などでは、シフト演算がビット操作に使用され、データの圧縮および伸張が行われます。
3. グラフィックスプログラミング: 3Dグラフィックスや画像処理において、シフト演算はピクセル操作や画像処理の最適化に使用されます。
4. 通信プロトコル: ネットワーク通信や通信プロトコルにおいて、データのエンコードやデコードにシフト演算が使用され、高速なデータ転送が実現されます。

シフト演算は、ビットレベルの操作であり、効率的で高速な計算を可能にするため、さまざまなビジネス領域で活用されています。

Pythonコード

number = 4
# 掛け算
multiplier = 2  # 2を掛ける場合
multiplied = number << multiplier
# 割り算
divisor = 2  # 2で割る場合
divided = number >> divisor
print(f"{number}を{multiplier}で掛けると{multiplied}になります。")
print(f"{number}を{divisor}で割ると{divided}になります。")

4を2で掛けると16になります。
4を2で割ると1になります。

コンピュータ特有のビット演算

ビット演算は、コンピュータにおいて整数をビット（0または1）単位で操作する演算です。主なビット演算には、以下の演算があります。

1. AND演算: 対応するビットが両方とも1の場合に1を返し、それ以外の場合は0を返します。例えば、5（二進数では0101）と3（二進数では0011）のAND演算は、0001となります。
2. OR演算: 対応するビットのどちらかが1の場合に1を返し、両方が0の場合は0を返します。例えば、5と3のOR演算は、0111となります。
3. XOR演算: 対応するビットが異なる場合に1を返し、同じ場合は0を返します。例えば、5と3のXOR演算は、0110となります。
4. NOT演算: 各ビットを反転させます。1は0に、0は1に変換されます。例えば、5のNOT演算は、1010となります。

ビット演算は、コンピュータの低レベルの操作で広く使用され、ビット単位のデータ処理に適しています。ビット演算を使用することで、データのマスク、ビット単位の制御、暗号化、ハッシュ関数の計算、データの圧縮など、さまざまなアルゴリズムが効率的に実装できます。

ビジネスの応用例

暗号化、ハッシュ関数の計算、データの圧縮などのアルゴリズムにおいて、ビット演算は効率的な計算を実現します。

• セキュリティ: 暗号化アルゴリズムやセキュリティプロトコルにおいて、ビット演算はキーマスク、データの暗号化、デジタル署名などのセキュリティ機能に使用されます。
• データ処理: ビット演算はデータのフィルタリング、変換、マスク処理に使用され、データベース、データ処理、通信プロトコルなどの分野で役立ちます。
• 組み込みシステム: マイクロコントローラや組み込みシステムでは、ビット演算が低レベルの制御やデバイス制御に使用され、リソース効率を改善させます。

Pythonコード

a = 5  # 0101 in binary
b = 3  # 0011 in binary
# AND演算
result_and = a & b
# OR演算
result_or = a | b
# XOR演算
result_xor = a ^ b
# NOT演算
result_not_a = ~a
# 結果の出力
print(f"{a} & {b} = {result_and} (AND operation)")
print(f"{a} | {b} = {result_or} (OR operation)")
print(f"{a} ^ {b} = {result_xor} (XOR operation)")
print(f"~{a} = {result_not_a} (NOT operation)")

5 & 3 = 1 (AND operation)
5 | 3 = 7 (OR operation)
5 ^ 3 = 6 (XOR operation)
~5 = -6 (NOT operation)

このコードは、ビット単位のAND、OR、XOR、NOT演算を実行します。ビット演算は、整数を2進数表現として扱い、各ビットごとに演算を行います。ビット演算は、整数を2進数表現として扱い、ビットごとに操作を行うため、高度なビット制御を実現します。

コンピュータ特有の論理演算

論理演算は、コンピュータにおいて真偽値（TrueまたはFalse）を操作する演算です。主な論理演算には、以下の演算があります。

1. AND演算: 両方の条件がTrueの場合に結果がTrueとなり、それ以外の場合はFalseを返します。例えば、xがTrueかつyがTrueの場合、x AND yはTrueです。
2. OR演算: どちらかの条件がTrueの場合に結果がTrueとなり、両方がFalseの場合はFalseを返します。例えば、xがTrueまたはyがTrueの場合、x OR yはTrueです。
3. NOT演算: 条件を反転させ、TrueはFalseに、FalseはTrueに変換します。例えば、xがTrueの場合、NOT xはFalseです。

論理演算は、条件分岐やフィルタリング、プログラムの制御構造においてとても重要です。真偽値を組み合わせて複雑な条件を評価し、プログラムの振る舞いを制御するのに役立ちます。

ビジネスの応用例

条件分岐やフィルタリング、データの検証などのプログラムの制御構造に使用されます。

• 条件分岐: プログラム内で特定の条件に基づいて異なるアクションを実行する場合、論理演算は条件式の評価に使用されます。
• データのフィルタリング: データセットから特定の条件を満たすデータを選択するために、論理演算はデータのフィルタリングに使用されます。
• セキュリティ: アクセス制御や認証システムにおいて、論理演算はユーザーの許可や認証の評価に使用されます。

Pythonコード

x = True
y = False
# AND演算
result_and = x and y
# OR演算
result_or = x or y
# NOT演算
result_not_x = not x
# 結果の出力
print(f"{x} and {y} = {result_and} (AND operation)")
print(f"{x} or {y} = {result_or} (OR operation)")
print(f"not {x} = {result_not_x} (NOT operation)")

True and False = False (AND operation)
True or False = True (OR operation)
not True = False (NOT operation)

このコードは、論理演算（AND、OR、NOT）を実行します。論理演算は、ブール値（TrueまたはFalse）に対して行われ、論理的な条件を評価します。論理演算は真偽値を組み合わせて複雑な条件を評価し、プログラムの振る舞いを制御するのに役立ちます。

方程式で図形を描く

数学的な方程式を使用して、2次元や3次元の図形を描画できます。

ビジネスの応用例

製品の設計や建築、CG映像の制作など、多岐にわたる分野で図形の描画は利用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 400)
y = x**2
plt.plot(x, y)
plt.title('y = x^2')
plt.show()

このコードは関数 y = x^2 のグラフを描画し、その形状を可視化します。グラフはMatplotlibを使用して表示され、x軸とy軸に対応する数値が表示されます。

方程式からグラフを描く

方程式を元に、変数の値の変化に応じた関数の値をグラフとして表現します。

ビジネスの応用例

データ解析やトレンドの確認、科学技術計算の結果の視覚化に利用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 400)
y = np.sin(x)
plt.plot(x, y)
plt.title('y = sin(x)')
plt.show()

このコードは関数 y = sin(x) のグラフを描画し、正弦関数の振る舞いを可視化します。グラフはMatplotlibを使用して表示され、x軸とy軸に対応する数値が表示されます。

直線の方程式を描く

直線の方程式は、一次方程式\(y = mx + c\) の形で表され、これをグラフとして描画できます。

ビジネスの応用例

売上のトレンドや株価の動向などを表す際に、直線の方程式が利用されることがあります。

Pythonコード

m = 2
c = 1
x = np.linspace(-10, 10, 400)
y = m*x + c
plt.plot(x, y)
plt.title('y = 2x + 1')
plt.show()

このコードは線形関数 y = 2x + 1 のグラフを描画し、直線の傾きとy切片を示す直線を可視化します。グラフはMatplotlibを使用して表示され、x軸とy軸に対応する数値が表示されます。

比例式と三角比

比例式:

比例式は、2つの量が一定の比率で変化する関係を示す数学的な式です。この式は一般的に以下のように表現されます。

\[y = kx\]

ここで、\(y\) は1つの量、\(x\) はもう一つの量、\(k\) は比例定数です。この式は、\(x\) が変化すると\(y\) も比例して変化します。例えば、速度と時間の関係、価格と数量の関係などが比例式で表現されます。

三角比:

三角比は、三角形の辺や角度に関連する数学的な比率です。主要な三角比には以下の3つがあります。

1. 正弦 (sin): 正弦は、ある角度の対向辺の長さを斜辺の長さで割った値です。正弦は次のように表現されます。 \[ \sin(\theta) = \frac{\text{対向辺の長さ}}{\text{斜辺の長さ}} \]
2. 余弦 (cos): 余弦は、ある角度の隣接辺の長さを斜辺の長さで割った値です。余弦は次のように表現されます。 \[ \cos(\theta) = \frac{\text{隣接辺の長さ}}{\text{斜辺の長さ}} \]
3. 接線 (tan): 接線は、ある角度の対向辺の長さを隣接辺の長さで割った値です。接線は次のように表現されます。 \[ \tan(\theta) = \frac{\text{対向辺の長さ}}{\text{隣接辺の長さ}} \]

ビジネスの応用例

建築や設計分野での三角形の形状や角度の計算、物流の最短経路計算などに使用されます。

• 建築・設計: 三角比は、建物や構造物の設計において角度や三角形の形状を計算するのに使用されます。例えば、屋根の勾配やトラス構造の計算に応用されます。
• 物流: 物流業界では、最短経路を計算する際に三角比を使用し、距離や方向の計算を行います。これにより、輸送コストを最適化できます。

Pythonコード

import math
# 与えられた角度
angle = 30  # degree
# 角度をラジアンに変換
angle_rad = math.radians(angle)
# sin、cos、tanの計算
sin_val = math.sin(angle_rad)
cos_val = math.cos(angle_rad)
tan_val = math.tan(angle_rad)
# 結果の表示
print(f"角度: {angle} 度")
print(f"sin({angle}°) = {sin_val:.2f}")  # 結果を小数点以下2桁まで表示
print(f"cos({angle}°) = {cos_val:.2f}")
print(f"tan({angle}°) = {tan_val:.2f}")

角度: 30 度
sin(30°) = 0.50
cos(30°) = 0.87
tan(30°) = 0.58

このコードは、与えられた角度（30度）に対して、sin、cos、tanの三角関数の値を計算し、その結果を小数点以下2桁まで表示しています。これらの三角関数は、角度と辺の長さの関係を数学的に表現するのに役立ちます。

三平方の定理

三平方の定理は、直角三角形において、直角を挟む2辺の長さの2乗の和が、斜辺の長さの2乗と等しいという数学的な法則です。これは直角三角形における基本的な関係式であり、ピタゴラスの定理とも呼ばれます。具体的には、以下の式で表されます。

\[a^2 + b^2 = c^2\]

ここで、\(a\) と \(b\) は直角を挟む2つの辺の長さを表し、\(c\) は斜辺の長さを表します。

ビジネスの応用例

土地の測量や建築物の設計時に、距離や高さを計算するために使用されます。

• 土地測量: 三平方の定理は、土地測量において、不動産の境界や地形の計測に使用されます。直角三角形の原理を応用して、距離や面積を正確に計算するのに役立ちます。
• 建築設計: 建築設計プロジェクトでは、建物の設計や配置において、三平方の定理を使用して正確な寸法と位置を計算します。

Pythonコード

import math
import matplotlib.pyplot as plt
a = 3
b = 4
c = math.sqrt(a**2 + b**2)
# Graph settings
plt.figure(figsize=(6, 6))
plt.plot([0, a], [0, 0], 'r', label='a')
plt.plot([0, 0], [0, b], 'g', label='b')
plt.plot([0, a], [0, b], 'b', label='c (Hypotenuse)')
plt.xlim(0, max(a, b) + 1)
plt.ylim(0, max(a, b) + 1)
plt.gca().set_aspect('equal', adjustable='box')
plt.legend()
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('Right Triangle Sides and Hypotenuse')
plt.grid(True)
# Display the result
print(f"斜辺の長さ: {c:.2f}")
# Show the graph
plt.show()

斜辺の長さ: 5.0

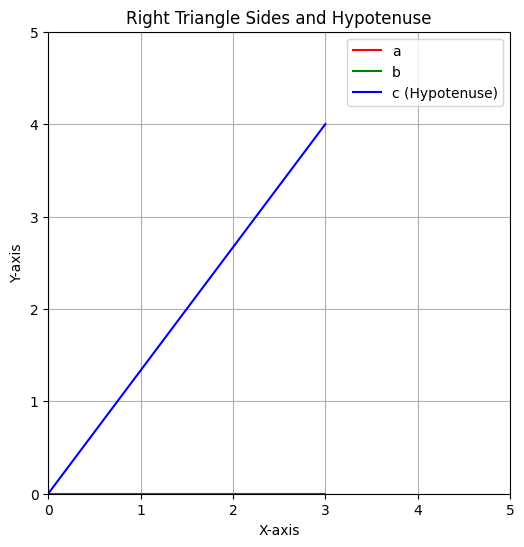
上記のPythonコード例では、直角三角形の2辺 \(a\) と \(b\) の長さを与えて、三平方の定理を用いて斜辺 \(c\) の長さを計算し、それをグラフで視覚化しています。この定理は、実世界の問題において距離や寸法を求めるための重要なツールです。

ベクトルの演算

ベクトルの演算:

ベクトルは、大きさ（長さ）と向きを持つ数学的な概念です。ベクトルの演算には以下の3つの主要な操作があります。

1. 加算 (Vector Addition): 2つのベクトルを足し合わせる操作です。ベクトルの各成分を対応する成分ごとに足し合わせます。
2. 減算 (Vector Subtraction): 2つのベクトルを引き算する操作です。ベクトルの各成分を対応する成分ごとに引き算します。
3. スカラー倍 (Scalar Multiplication): ベクトルにスカラー（実数）を掛ける操作です。ベクトルの各成分にスカラーを掛けます。

ビジネスの応用例

物理や工学の分野で、力や速度などのベクトル量を計算する際に使用されます。

• 物理学: 物体の速度、加速度、力などのベクトル量を計算するために使用されます。たとえば、自動車の速度ベクトルと風速ベクトルを合成して、風を受ける車の速度を計算することがあります。
• 工学: 構造物の応力解析や電気回路の計算など、さまざまな工学分野でベクトル演算が必要です。たとえば、橋の支持構造のベクトル力学を使用して設計することがあります。

Pythonコード

import numpy as np
vector_a = np.array([1, 2])
vector_b = np.array([3, 4])
print(vector_a + vector_b)
print(vector_a - vector_b)
print(2 * vector_a)

[4 6]
[-2 -2]
[2 4]

上記のPythonコード例では、2つのベクトル vector_a と vector_b を加算、減算し、スカラー倍を計算しています。これらの演算は、ベクトルを使用して物理的な量やデータを効率的に処理するためにとても役立ちます。

ベクトル方程式

ベクトル方程式は、ベクトルを使用して方程式を表現する方法です。通常、ベクトル方程式は以下の形式で表されます。

\[ \mathbf{v} = \mathbf{a} + t \cdot \mathbf{d} \]

ここで、各記号の意味は次のとおりです。

• \( \mathbf{v} \): 位置ベクトル（点を表すベクトル）
• \( \mathbf{a} \): 始点ベクトル（直線や曲線の始点を表すベクトル）
• \( t \): パラメータ（スカラー値）
• \( \mathbf{d} \): 方向ベクトル（直線や曲線の進行方向を表すベクトル）

この方程式は、\( t \) の値を変えることで、直線や曲線上の異なる点を表現できます。

ビジネスの応用例

3D モデリングやCGの制作、航空機の飛行経路の設計などに使用されます。

• 3D モデリング: 3Dオブジェクトの位置や移動を表現するためにベクトル方程式が使用されます。たとえば、アニメーションソフトウェアでキャラクターの動きを制御するのに役立ちます。
• 航空機の飛行経路設計: 航空機の飛行経路を計画する際に、出発地点から目的地点までの航空機の位置をベクトル方程式を使用して表現します。

Pythonコード

import matplotlib.pyplot as plt
# ベクトルの定義
vector_a = np.array([1, 2])
vector_b = np.array([4, 5])
# プロット
plt.figure(figsize=(6, 6))
plt.quiver(0, 0, vector_a[0], vector_a[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector A')
plt.quiver(0, 0, vector_b[0], vector_b[1], angles='xy', scale_units='xy', scale=1, color='g', label='Vector B')
# ベクトルの加算結果を描画
result = vector_a + vector_b
plt.quiver(0, 0, result[0], result[1], angles='xy', scale_units='xy', scale=1, color='b', label='Result')
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.legend()
plt.grid(True)
plt.title('Visualization of vector operations')
plt.show()

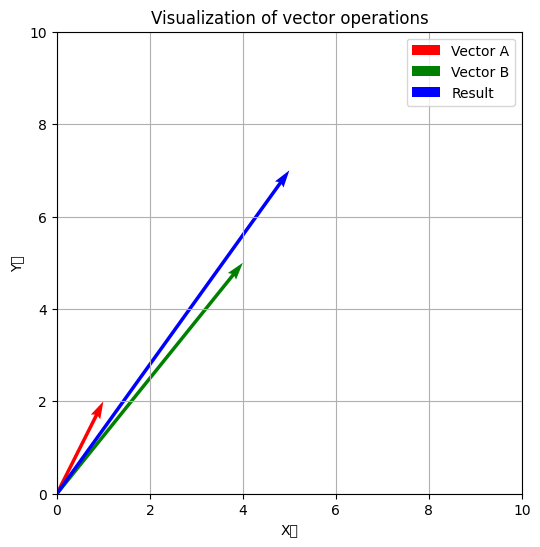
上記のPythonコード例では、ベクトルAとベクトルBを視覚的に表現しています。これらのベクトルを加算することで、新しいベクトル（”Result”として表示）を生成し、その結果をプロットしています。ベクトル方程式は、ベクトルの位置や移動を効果的に扱うために使用されます。

ベクトルの内積

ベクトルの内積は、2つのベクトルの成分ごとの積を合計する操作です。具体的には、ベクトル \( \mathbf{a} \) とベクトル \( \mathbf{b} \) の内積は以下のように計算されます。

\[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta \]

ここで、各記号の意味は次のとおりです。

• \( \mathbf{a} \cdot \mathbf{b} \): ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の内積
• \( |\mathbf{a}| \): ベクトル \( \mathbf{a} \) の大きさ（ノルム）
• \( |\mathbf{b}| \): ベクトル \( \mathbf{b} \) の大きさ（ノルム）
• \( \theta \): ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) のなす角（ラジアン）

ベクトルの内積は、2つのベクトルがどれだけ同じ方向に向いているかを示し、ベクトル同士の類似性や関連性を評価するのに役立ちます。内積が正の場合、ベクトルは似た方向に向いており、負の場合は逆向きに向いています。また、内積がゼロの場合、ベクトルは直交しています。

ビジネスの応用例

機械学習のアルゴリズムや、データの類似度を計算する際に使用されます。

• 機械学習: 特徴ベクトル同士の内積を計算して、類似性を評価し、クラスタリングや分類などのタスクに使用します。
• データベース検索: 文書ベクトルの内積を計算して、文書の類似性を評価し、情報検索に使用します。

Pythonコード

vector_a = np.array([1, 2])
vector_b = np.array([3, 4])
dot_product = np.dot(vector_a, vector_b)
print(dot_product)

11

上記のPythonコード例では、ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の内積（ドット積）を計算し、その結果を表示しています。ベクトルの内積は、ベクトル同士の関係性を数値的に捉えるための重要な操作です。

ベクトルの外積

ベクトルの外積は、2つのベクトルから新しいベクトルを生成する操作で、その結果のベクトルは元の2つのベクトルに垂直です。ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の外積を \( \mathbf{c} \) と表現すると、次のようになります。

\[ \mathbf{c} = \mathbf{a} \times \mathbf{b} \]

外積の結果のベクトル \( \mathbf{c} \) の大きさや向きは、\( \mathbf{a} \) と \( \mathbf{b} \) の間の平面に依存します。外積は、ベクトル間の「回転」や「垂直性」を評価するのに役立ちます。

ビジネスの応用例

物理学や工学の分野で、特に電磁気学や力のモーメントの計算に使用されます。

• 物理学: 電磁気学や力学の問題において、モーメントやトルクの計算に使用されます。
• 工学: 機械工学や材料工学において、応力とひずみの関係を理解し、設計を行う際に使用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])
cross_product = np.cross(vector_a, vector_b)
# 3Dグラフの設定
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 原点から法線ベクトルを描画
ax.quiver(0, 0, 0, cross_product[0], cross_product[1], cross_product[2], color='b')
# 軸ラベル
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')
plt.show()

上記のPythonコード例では、ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の外積を計算し、その結果のベクトルを3Dグラフで表示しています。外積の結果は、元の2つのベクトルが張る平面に垂直であり、その向きや大きさは2つのベクトルの相対的な配置に依存します。外積は、ベクトルの幾何学的な特性を解析する際に重要なツールです。

行列とは？

行列は、数や数式を矩形状に配置したものです。行と列からなり、通常、数値や変数が格納されています。行列は数学の多くの分野で利用され、特に線形代数において重要な役割を果たします。

行列は以下のように表現されます。

\[ A = \begin{bmatrix}
a_{11} & a_{12} & \ldots & a_{1n} \
a_{21} & a_{22} & \ldots & a_{2n} \
\vdots & \vdots & \ddots & \vdots \
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{bmatrix} \]

ここで、\( a_{ij} \) は行列内の各要素を表します。行列は行と列のインデックスによって参照され、\( m \) は行の数、\( n \) は列の数です。

ビジネスの応用例

機械学習やディープラーニングのアルゴリズムの中核に行列計算が存在します。また、金融のリスク評価や、データの圧縮、画像処理など、多岐にわたる分野で活用されます。

• 機械学習とディープラーニング: ニューラルネットワークの重み、データの表現、特徴量の変換など、多くの機械学習アルゴリズムで行列計算が使用されます。
• 金融: リスク評価モデルや資産ポートフォリオの最適化に行列計算が適用されます。
• データ分析: データセットの処理、データの圧縮、主成分分析など、データ分析の多くの手法で行列が利用されます。

Pythonコード

import numpy as np
matrix_a = np.array([[1, 2], [3, 4]])
print(matrix_a)

[[1 2]
 [3 4]]

上記のPythonコード例では、NumPyライブラリを使用して2×2の行列 matrix_a を作成し、その内容を表示しています。行列はデータを整理し、さまざまな数学的操作を行うための強力なツールです。

行列の演算

行列の演算は、数学的な操作を行うための方法です。主に加算、減算、乗算の3つの基本的な演算があります。これらの演算は、行列の要素同士を操作する方法です。

1. 加算（Summation）:
   行列の加算は、対応する要素同士を足し合わせる操作です。行列Aと行列Bがある場合、それぞれの要素を足し合わせた新しい行列を得ることができます。 例えば、以下のコードでは、行列Aと行列Bを加算して、sum_matrixという新しい行列を得ています。

   sum_matrix = matrix_a + matrix_b

結果は次のようになります。

   Sum:
   [[3 2]
    [3 6]]

2. 乗算（Multiplication）:
   行列の乗算は、特定のルールに基づいて行われる操作で、通常の数値の乗算とは異なります。行列Aと行列Bの乗算は、行列Aの行と行列Bの列を組み合わせて新しい行列を作成します。 以下のコードでは、行列Aと行列Bを乗算して、product_matrixという新しい行列を得ています。

   product_matrix = np.dot(matrix_a, matrix_b)

結果は次のようになります。

   Product:
   [[2 4]
    [6 8]]

ビジネスの応用例

ビジネスの応用例としては、データベースのクエリ処理や、グラフ理論の問題、最適化問題の解法など、さまざまな場面で行列の演算が必要です。例えば、データベースクエリでは、多次元データを扱う際に行列を使用してクエリの結果を計算したり、最適化問題では行列演算を使用して最適な解を見つけたりします。

Pythonコード

matrix_b = np.array([[2, 0], [0, 2]])
sum_matrix = matrix_a + matrix_b
product_matrix = np.dot(matrix_a, matrix_b)
print("Sum:")
print(sum_matrix)
print("Product:")
print(product_matrix)

Sum:
[[3 2]
 [3 6]]
Product:
[[2 4]
 [6 8]]

Pythonコードの例では、NumPyライブラリを使用して行列演算を実行しています。行列の加算は+演算子を使用し、行列の乗算はnp.dot()関数を使用しています。このようなコードを使って、行列演算を実行できます。

図形の一次変換

図形の一次変換は、図形を移動、回転、拡大縮小などの変換を行うことを指します。この変換は、通常行列を使用して表現されます。

1. 移動、回転、拡大縮小:
   • 移動（Translation）: 図形を平行移動させます。つまり、図形内のすべての点を同じ距離と方向に移動させます。たとえば、図形を右に2単位、上に3単位移動させることができます。
   • 回転（Rotation）: 図形を中心を軸に回転させます。図形の各点が中心を中心に一定の角度だけ回転します。
   • 拡大縮小（Scaling）: 図形を大きくしたり小さくしたりします。各点の座標をスケールファクターによって変更します。
2. 行列を用いた表現:
   これらの一次変換は、行列を使用して簡潔に表現できます。行列は、図形内の各点の座標に変換を適用するのに役立ちます。行列をかけることで、一度に多くの点に対して変換を適用できます。

ビジネスの応用例

グラフィックデザインやゲーム開発、映像制作などの分野で、物体やキャラクターの位置や姿勢を調整する際に一次変換が用いられます。

• グラフィックデザイン: 画像や図形の位置を調整し、アニメーションやエフェクトを作成するために使用されます。
• ゲーム開発: ゲーム内のキャラクターやオブジェクトの動きや姿勢を制御するために使用されます。
• 映像制作: 特殊効果やアニメーションの作成に使用され、映画やアニメーションの制作において重要な役割を果たします。

Pythonコード

import matplotlib.pyplot as plt
# Original shape
x = [0, 1, 1, 0, 0]
y = [0, 0, 1, 1, 0]
plt.plot(x, y, label="Original")
# Transformation matrix
transformation = np.array([[2, 0], [0, 1.5]])
transformed = np.dot(transformation, [x, y])
plt.plot(transformed[0], transformed[1], label="Transformed")
plt.legend()
plt.show()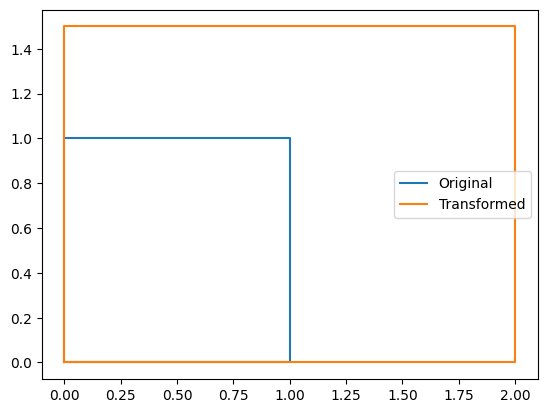

上記Pythonコードは、一次変換の一例です。matplotlib.pyplotを使用して、元の図形と変換後の図形をプロットしています。変換は行列transformationを使用して行われ、元の図形の座標を変換し、変換後の座標をプロットしています。このようにして、図形の一次変換を視覚的に表現できます。

集合とは？

集合とは、異なる要素が重複せず、一度だけ含まれる要素のまとまりを表す数学的な概念です。集合は、その中に含まれる要素を順序なしで持ち、要素が重複しないことが特徴です。集合は、日常的な問題解決や論理的思考において、要素のグループ化と集合間の関係を表現するのに役立ちます。

特徴:

• 重複しない要素: 集合内の要素は一度だけ含まれ、同じ要素が重複しません。たとえば、{1, 2, 3, 4, 5} は集合であり、同じ要素が複数回含まれることはありません。
• 順序なし: 集合内の要素は順序を持たず、要素の順序が変わっても同じ集合です。つまり、{1, 2, 3} と {3, 2, 1} は同じ集合です。

ビジネスの応用例

データベースの操作、特にSQLのクエリでの集合演算や、マーケティングのターゲットセグメントの選定などで集合の考え方が活用されます。

集合の考え方は、ビジネスやデータ処理のさまざまな分野で役立ちます。

• データベース操作: データベースのクエリで集合演算を使用して、データの絞り込みや結合を行います。SQLクエリにおけるJOIN操作やUNION操作などが集合演算の一例です。
• マーケティング: マーケティングでは、ターゲットセグメントの選定や顧客のセグメンテーションに集合の考え方を応用します。たとえば、特定の商品を購入した顧客の集合を特定し、それに基づいてマーケティング戦略を立案できます。

Pythonコード

set_a = {1, 2, 3, 4}
set_b = {3, 4, 5, 6}
union_set = set_a | set_b
intersection_set = set_a & set_b
print(f"Union: {union_set}")
print(f"Intersection: {intersection_set}")

Union: {1, 2, 3, 4, 5, 6}
Intersection: {3, 4}

上記のPythonコードでは、Pythonの集合を操作しています。

• set_a と set_b という2つの集合を定義しています。
• union_set 変数には、2つの集合の和集合（両方の集合の要素を含む集合）が格納されます。
• intersection_set 変数には、2つの集合の積集合（両方の集合に共通する要素からなる集合）が格納されます。

コードを実行すると、和集合と積集合が計算され、それぞれの結果が表示されます。和集合には2つの集合のすべての要素が含まれ、積集合には共通する要素だけが含まれます。

Union: {1, 2, 3, 4, 5, 6}
Intersection: {3, 4}

これにより、集合演算がどのように機能し、集合の要素が操作されるかが示されています。

順列と組み合わせ

順列と組み合わせは、数学的な概念で、異なるアイテムの集合から特定の要件を満たすアイテムのグループを作成する方法を計算するために使用されます。

順列（Permutations）:
順列は、n個のアイテムの集合からr個のアイテムを選び、そのアイテムを異なる順番で並べる方法の数を表します。順列では順序が重要です。つまり、選んだアイテムを異なる順番で並べることで異なる順列が得られます。

例: A、B、Cという3つのアイテムから2つのアイテムを選んで順列を計算すると、 (‘A’, ‘B’)、(‘A’, ‘C’)、(‘B’, ‘A’)、(‘B’, ‘C’)、(‘C’, ‘A’)、(‘C’, ‘B’) の6つの順列が得られます。

組み合わせ（Combinations）:
組み合わせは、n個のアイテムの集合からr個のアイテムを選び、順序を考慮せずにグループを作成する方法の数を表します。組み合わせでは、選んだアイテムの順序は考慮されません。つまり、同じアイテムの組み合わせが異なる順序で表示されることはありません。

例: A、B、Cという3つのアイテムから2つのアイテムを選んで組み合わせを計算すると、 (‘A’, ‘B’) と (‘A’, ‘C’)、(‘B’, ‘C’) の3つの組み合わせが得られます。

ビジネスの応用例

商品の並べ方の最適化や、マーケティングキャンペーンの組み合わせの検討、株のポートフォリオの組み合わせ選定などで順列や組み合わせの考え方が利用されます。

順列と組み合わせの考え方は、ビジネスにおいてさまざまな場面で役立ちます。

• 商品の並べ方の最適化: 商品陳列の最適な順序を決定するために順列を使用できます。特定の商品をどのような順序で陳列するかが、売上や顧客の満足度に影響を与えることがあります。
• マーケティングキャンペーンの組み合わせ: マーケティングキャンペーンの要素（広告、プロモーション、コンテンツなど）を組み合わせて最適なキャンペーン戦略を決定するために組み合わせを使用できます。
• 株のポートフォリオの組み合わせ選定: 株式投資の際に、異なる株式からポートフォリオを構築するための最適な組み合わせを計算するのに組み合わせが役立ちます。

Pythonコード

import itertools
items = ['A', 'B', 'C']
permutations = list(itertools.permutations(items, 2))
combinations = list(itertools.combinations(items, 2))
print(f"Permutations: {permutations}")
print(f"Combinations: {combinations}")

Permutations: [('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B')]
Combinations: [('A', 'B'), ('A', 'C'), ('B', 'C')]

上記のPythonコードでは、Pythonの itertools ライブラリを使用して順列と組み合わせを計算しています。

• items リストには、(‘A’, ‘B’, ‘C’) という3つのアイテムが含まれています。
• itertools.permutations() 関数を使用して、アイテムから2つの順列を計算し、permutations リストに格納します。
• itertools.combinations() 関数を使用して、アイテムから2つの組み合わせを計算し、combinations リストに格納します。

コードを実行すると、計算された順列と組み合わせが表示されます。

Permutations: [('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B')]
Combinations: [('A', 'B'), ('A', 'C'), ('B', 'C')]

このようにして、順列と組み合わせが計算され、異なる順序や順不同での結果が得られます。

数学的確率と統計的確率

数学的確率と統計的確率は、確率の考え方を異なる方法で表現する方法です。

数学的確率:
数学的確率は、ある事象が起こる確率を数学的に定義する方法です。これは、理論的なモデルや公式を使用して確率を計算します。たとえば、公正なサイコロを振る場合、各目の出る確率は1/6（約0.1667）です。この確率は、サイコロの各面が均等に出ることが数学的に確定的に証明されたものです。

統計的確率:
統計的確率は、実際のデータや観測に基づいて事象の確率を推定する方法です。統計的確率は、実際の試行や観測結果から確率を導き出します。たとえば、サイコロを1000回振って、3が出た回数を数えてその割合を計算することで、3が出る確率を推定します。

ビジネスの応用例

商品の売上予測、株価の動きの予測、広告のクリック確率の予測など、多岐にわたる分野で確率の考え方が活用されます。

確率の考え方はビジネスにおいて多くの分野で利用されます。

• 商品の売上予測: 過去の売上データをもとに、将来の売上を統計的確率を用いて予測します。
• 株価の動きの予測: 過去の株価データや市場動向から、将来の株価動向を統計的確率を用いて予測します。
• 広告のクリック確率の予測: ウェブ広告のクリック率を統計的確率を用いて推定し、広告キャンペーンを最適化します。

Pythonコード

# Example: Rolling a die
import random
# Mathematical probability
math_prob = 1/6
# Statistical probability (simulating 1000 rolls)
rolls = [random.randint(1, 6) for _ in range(1000)]
stat_prob = rolls.count(3) / 1000
print(f"Mathematical Probability: {math_prob}")
print(f"Statistical Probability: {stat_prob}")

Mathematical Probability: 0.16666666666666666
Statistical Probability: 0.159

上記のPythonコードは、数学的確率と統計的確率の比較を示す例です。

• math_prob 変数には、数学的確率が1/6（約0.1667）が格納されています。これは、サイコロを振ったときに3の目が出る確率です。
• stat_prob 変数には、統計的確率が1000回のサイコロ振りの結果から計算された確率が格納されています。この確率は、3が出た回数をサイコロ振りの総回数で割ったものです。

コードを実行すると、数学的確率と統計的確率が表示され、統計的確率は数学的確率に近い値であることが示されます。

Mathematical Probability: 0.16666666666666666
Statistical Probability: 0.159

この例では、サイコロを1000回振って統計的確率を推定しましたが、試行回数を増やすことでより正確な結果を得ることができます。統計的確率は、実際のデータに基づいて不確実性を扱うためにとても有用です。

積の法則と和の法則

積の法則と和の法則は、確率論において重要な法則です。

• 積の法則（Product Rule）:
  • 積の法則は、2つの独立な事象AとBが同時に起こる場合の方法の総数を求める法則です。独立な事象とは、一つの事象が他の事象に影響を与えないことを意味します。積の法則では、事象Aと事象Bが同時に起こる確率を計算するために、それぞれの事象の起こる方法の数を掛け合わせます。
  • 例1: おにぎりとドリンク 弁当屋に行くと、3種類のおにぎり（しゃけ、たらこ、梅）と2種類のドリンク（お茶、ジュース）が売られています。ランチに1つのおにぎりと1つのドリンクを選ぶとすると、選べる組み合わせは何通りあるでしょうか？ 積の法則を使うと、おにぎりの選び方3通り × ドリンクの選び方2通り = 6通りの組み合わせがあります。
  • 例2: 服と靴 クローゼットには、2種類のシャツ（赤、青）と3種類の靴（スニーカー、ブーツ、サンダル）があります。今日のコーディネートとしてシャツ1枚と靴1足を選ぶ場合、何通りの組み合わせが考えられるでしょうか？ 積の法則を使用すると、シャツの選び方2通り × 靴の選び方3通り = 6通りの組み合わせが考えられます。

• 和の法則（Sum Rule）:
  • 和の法則は、2つの排他的な事象AとBのいずれかが起こる場合の方法の総数を求める法則です。排他的な事象とは、同時には起こりえない事象のことを指します。和の法則では、事象Aまたは事象Bが起こる確率を計算するために、それぞれの事象の起こる方法の数を足し合わせます。
  • 例1: 宝箱とキー 2つの部屋があり、1つ目の部屋には2つの宝箱、2つ目の部屋には3つの宝箱があります。部屋を1つ選び、その中の宝箱を1つ開けることができるとします。宝箱を1つ開ける選択肢は何通りあるでしょうか？ 和の法則により、1つ目の部屋の宝箱の選び方2通り + 2つ目の部屋の宝箱の選び方3通り = 5通りの選択肢が考えられます。
  • 例2: アイスクリーム アイスクリーム屋には、バニラとチョコレートの2つのフレーバーがあります。そして、その隣の別のアイスクリーム屋には、ストロベリーとマンゴーの2つのフレーバーがあります。1つの店舗から1つのフレーバーを選ぶ場合、選べるフレーバーは何通りあるでしょうか？ 和の法則を使うと、最初の店のフレーバー選び方2通り + 次の店のフレーバー選び方2通り = 4通りの選択肢があります

ビジネスの応用例

製品の組み合わせの可能性や、マーケティングキャンペーンの組み合わせ選定に利用できます。

• 製品の組み合わせ: 製品Aと製品Bの組み合わせを考える際、積の法則を用いてそれぞれの製品のバリエーションを掛け合わせ、可能な製品組み合わせの総数を求めることができます。
• マーケティングキャンペーン: マーケティングキャンペーンAまたはBが成功する確率を求める際、和の法則を用いてそれぞれのキャンペーンの成功確率を足し合わせることができます。

Pythonコード

# Sample for Product Rule
colors = ['Red', 'Blue']
sizes = ['S', 'M', 'L']
combinations = [(color, size) for color in colors for size in sizes]
print("Product Rule Sample:", combinations)
# Sample for Sum Rule
red_or_s = len([comb for comb in combinations if comb[0] == 'Red' or comb[1] == 'S'])
print("Sum Rule Sample:", red_or_s)

Product Rule Sample: [('Red', 'S'), ('Red', 'M'), ('Red', 'L'), ('Blue', 'S'), ('Blue', 'M'), ('Blue', 'L')]
Sum Rule Sample: 4

Pythonコードは、積の法則と和の法則のサンプルを示しています。

• colors リストと sizes リストには、それぞれ色とサイズのバリエーションが含まれています。
• combinations リスト内包表記を使用して、色とサイズの組み合わせを積の法則を用いて計算し、combinations に格納されます。
• red_or_s 変数は、和の法則を用いて、「Red」の色または「S」のサイズが選ばれる確率を計算します。これは、「Red」または「S」のいずれかが選ばれる組み合わせの数を計算しています。

コードを実行すると、積の法則と和の法則がそれぞれサンプルとして示されます。

積の法則のサンプル:

Product Rule Sample: [('Red', 'S'), ('Red', 'M'), ('Red', 'L'), ('Blue', 'S'), ('Blue', 'M'), ('Blue', 'L')]

和の法則のサンプル:

Sum Rule Sample: 4

これにより、積の法則ではすべての組み合わせが計算され、和の法則では排他的な結果が計算されることが示されています。

モンテカルロ法

モンテカルロ法は、乱数を使用して数値的な問題を解決する手法の一つで、確率的な問題や複雑な数学的モデルを解析するために用いられます。

• モンテカルロ法の概要:
  • モンテカルロ法は、ランダムなデータ生成やシミュレーションを用いて、数学的な問題に対する近似解を求める方法です。この手法は、解析的な解法が難しい問題や高次元の問題に対して特に有用です。モンテカルロ法の基本的なアイデアは、ランダムなサンプルを生成し、これらのサンプルを用いて問題の解を近似することです。ランダム性を利用することで、確率的な問題や多次元空間での問題に対処できます。
• 例1: コイン投げで円の面積を求める
  • 広い広場に大きな正方形のシートが敷かれているとします。このシートの中には、円が描かれています。円の中心は正方形の中心と一致しています。今、この円の面積を知りたいと思ったとき、モンテカルロ法を使って求める方法があります。コインをたくさん、ランダムにこの正方形のシートに投げます。そして、コインが円の中に落ちた数と、円の外に落ちた数を数えます。コインが全体で何回円の中に落ち、何回円の外に落ちたかを使って、円の面積の近似値を計算できます。
• 例2: 誕生日の問題
  • あるクラスに30人の生徒がいるとします。そのクラスで2人以上の生徒が同じ誕生日を持っている確率を知りたいとします。実際には計算が複雑になりますが、モンテカルロ法を使って近似的に求めることができます。ランダムに30人分の誕生日を選び、その中で2人以上同じ誕生日を持っているかどうかを確認します。これを何千回、何万回と繰り返して、同じ誕生日を持つ生徒がいた場合の割合を計算します。この割合が、2人以上が同じ誕生日を持つ確率の近似値となります。

ビジネスの応用例

金融市場のリスク評価や、製造工程の最適化、プロジェクト管理のシミュレーションなどで利用されます。

モンテカルロ法はビジネス分野でも広く利用されます。

• 金融市場のリスク評価: 株式や債券の価格変動のモデリングやリスク評価に使用されます。将来の価格変動をシミュレーションし、ポートフォリオのリスクを評価します。
• 製造工程の最適化: 製造プロセスの効率を最適化するために使用されます。材料や機械の特性をランダムに変動させ、最適な製品設計や生産スケジュールを見つけます。
• プロジェクト管理のシミュレーション: プロジェクトの進捗やリソースの管理をシミュレーションし、プロジェクトの成功確率や遅延のリスクを評価します。

Pythonコード

import random
# Estimate pi using Monte Carlo
num_points = 10000
inside_circle = 0
for _ in range(num_points):
    x, y = random.random(), random.random()
    if x**2 + y**2 <= 1:
        inside_circle += 1
estimated_pi = 4 * inside_circle / num_points
print("Estimated Pi:", estimated_pi)

Estimated Pi: 3.1432

Pythonコードは、円周率 π の近似計算を行うモンテカルロ法のサンプルです。以下はコードの詳細な説明です。

• num_points 変数には、乱数生成の回数を指定します。この例では10000回の乱数生成を行います。
• inside_circle 変数は、単位円（半径1の円）の内部に乱数が落ちる回数をカウントするための変数です。
• ループを用いて、指定した回数だけ乱数 x と y を生成し、これらの乱数が単位円内に落ちるかどうかを判定します。判定は x^2 + y^2 <= 1 という条件で行います。
• 内部に落ちた乱数の回数をカウントし、最終的に円周率 π の近似値を計算します。この計算は 4 * inside_circle / num_points で行います。

コードを実行すると、近似された円周率 π の値が表示されます。例えば、Estimated Pi: 3.1432 のような値が得られます。乱数を使用して円周率を推定することが、モンテカルロ法の一例です。

統計学

統計とは

統計は、データに関する情報を収集し、整理・解析してその結果を活用する学問・手法のことです。

統計の概要:
統計は、データを収集し、整理、要約し、そのデータから意味fulな情報を抽出するための学問です。統計は主に2つの側面から成り立っています。

• 記述統計学（Descriptive Statistics）: データを要約し、グラフ化してデータの特徴や傾向を理解するための方法です。平均値、中央値、分散、標準偏差などの統計的指標が含まれます。
• 推測統計学（Inferential Statistics）: サンプルデータをもとに、全体の母集団に関する推論を行う方法です。信頼区間、仮説検定、回帰分析などが含まれます。

ビジネスの応用例

市場調査、製品の品質管理、販売予測など、多くのビジネスプロセスで統計的手法が利用されます。

統計的手法はビジネスにおいて広く活用されます。

• 市場調査: 消費者の嗜好を調査し、市場セグメンテーションや新製品の評価に統計を使用します。
• 製品の品質管理: 製品の品質制御や不良品の発見に統計的プロセス制御（SPC）を用います。
• 販売予測: 過去の販売データから将来の販売量を予測するために、時系列分析や予測モデルが利用されます。

Pythonコード

import statistics
data = [2, 5, 9, 12, 13, 7, 10, 11, 12, 9, 6]
mean = statistics.mean(data)
print("Mean of Data:", mean)

Mean of Data: 8.727272727272727

Pythonコードは、統計の基本的な操作の一例です。

• statistics ライブラリを使用して、データセット data の平均値（平均）を計算します。
• statistics.mean(data) は、与えられたデータセット data の平均値を計算し、その結果を mean 変数に格納します。
• print("Mean of Data:", mean) は、計算された平均値を表示します。

コードを実行すると、データセット data の平均値が表示されます。例えば、Mean of Data: 8.727272727272727 のようになります。このコードは統計的な基本操作の一つで、データの特性を理解し、意思決定や問題解決に役立てるのに役立ちます。

母集団と標本

母集団と標本は統計学で重要な概念で、データ分析や調査の際に使用されます。

母集団（Population）:
母集団は、研究や分析の対象となる全体の集合を指します。これは、全ての対象やデータポイントが含まれる集合であり、調査や分析を行いたい対象全体を表します。母集団はしばしばとても大きいため、全てのデータを調査することが難しい場合があります。

標本（Sample）:
標本は、母集団から選ばれる部分集合です。標本は、母集団の特性を推測するために使用されます。標本は母集団全体を代表し、母集団の特性や特定の性質について情報を提供することを目的としています。標本は母集団から無作為に選ばれることが一般的で、ランダムな選択がバイアスを避けるために重要です。

ビジネスの応用例

顧客満足度調査や品質検査などで、全体を調査するのが困難な場合に標本を取って分析します。

母集団と標本はビジネス分野でも広く活用されます。

• 顧客満足度調査: 顧客全体の意見を収集するのは難しいため、一部の顧客からなる標本を対象に調査を行い、母集団全体の満足度を推測します。
• 品質検査: 製品全量の検査が困難な場合、一部の製品を標本として選び、品質を評価し、母集団の品質を推定します。

Pythonコード

population = list(range(1000))
sample = random.sample(population, 50)
print("Sample:", sample)

Sample: [337, 145, 116, 216, 601, 204, 528, 288, 476, 875, 563, 31, 737, 289, 400, 257, 130, 510, 127, 869, 543, 200, 539, 920, 422, 975, 923, 60, 123, 625, 676, 329, 426, 797, 681, 954, 556, 307, 117, 817, 760, 370, 879, 272, 320, 626, 471, 555, 508, 287]

Pythonコードは、標本の作成を示すサンプルです。

• population リストは0から999までの整数を含んでおり、これが母集団を表しています。
• random.sample(population, 50) は、population からランダムに50個の要素を選んで標本を作成します。この操作により、母集団から無作為に選ばれた50個のデータポイントが sample 変数に格納されます。
• print("Sample:", sample) は、作成された標本を表示します。

このコードは、母集団からランダムに標本を選んでデータのサブセットを作成する例です。標本は母集団の特性を推測するために使用されることがあります。

平均値、中央値、最頻値

平均値、中央値、最頻値は、データセットの特性を理解し、データの中心傾向や頻度分布を調べるための統計的な指標です。

平均値（Mean）:
平均値は、データセット内のすべての数値の合計を、データの総数で割った値です。平均はデータの中心傾向を表し、データセット内の値の平均的な大きさを示します。平均は数値の合計を全体の数で均等に分配した値です。

中央値（Median）:
中央値は、データを昇順に並べたときに、中央に位置する値です。つまり、データを小さい値から大きい値に並べ替えたときに、ちょうど中央に来る値です。中央値は外れ値（極端に大きいまたは小さい値）の影響を受けにくく、データの中央に位置する中心傾向の指標です。

最頻値（Mode）:
最頻値は、データセット内で最も頻繁に出現する値です。つまり、データ内で最も多くの回数現れる値を指します。最頻値はデータセット内の頻度分布を表し、特にカテゴリカルデータや離散的なデータの中心傾向を示すのに役立ちます。

ビジネスの応用例

売上データの分析、顧客の購買履歴の分析、従業員の評価など、多岐にわたる分野でこれらの統計的指標が利用されます。

統計的指標はビジネス分野でも広く活用されます。

• 売上データの分析: 平均売上を計算して、売上の平均的な大きさを理解します。
• 顧客の購買履歴の分析: 中央値を使用して、顧客の購買額の中央値を把握し、顧客層を理解します。
• 従業員の評価: 最頻値を使用して、従業員の評価において最も一般的な評価値を特定します。

Pythonコード

median = statistics.median(data)
mode = statistics.mode(data)
print("Median of Data:", median)
print("Mode of Data:", mode)

Median of Data: 9
Mode of Data: 9

Pythonコードは、データセット data の中央値と最頻値を計算し、表示する例です。

• statistics.median(data) は、データセット data の中央値を計算し、その結果を median 変数に格納します。
• statistics.mode(data) は、データセット data の最頻値を計算し、その結果を mode 変数に格納します。
• 最終的に、計算された中央値と最頻値が表示されます。

このコードは、データセット内の中央値と最頻値を計算して、データセットの中心傾向と頻度分布を調べるための手法の一例です。

度数分布

度数分布は、データセット内の個々の値（または値の範囲）が、データ内で何回出現するかをまとめたものです。これは、データセット内の値の分布を視覚的に理解するための重要な手法です。度数分布は通常、表やヒストグラムとして表示され、データ内のパターンやトレンドを把握するのに役立ちます。

ビジネスの応用例

商品の売上ランキング、ウェブサイトのページビュー数、顧客の年齢分布など、データの分布を視覚的に理解する際に度数分布が利用されます。

度数分布はビジネス分野でも幅広く活用されます。

• 商品の売上ランキング: 商品別の売上回数を分析して、売上の主要な寄与要因を特定します。
• ウェブサイトのページビュー数: ウェブサイト上の各ページが訪問された回数を把握して、人気のあるコンテンツを特定します。
• 顧客の年齢分布: 顧客データから年齢グループ別の分布を作成し、ターゲットセグメントを特定します。

Pythonコード

import matplotlib.pyplot as plt
from collections import Counter
data = [1, 2, 2, 3, 4, 4, 4, 5]
# Calculate the frequency distribution of the data
frequency = Counter(data)
# Plot a histogram
plt.bar(frequency.keys(), frequency.values())
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Frequency Distribution of Data')
plt.show()

Frequency Distribution: Counter({9: 2, 12: 2, 2: 1, 5: 1, 13: 1, 7: 1, 10: 1, 11: 1, 6: 1})

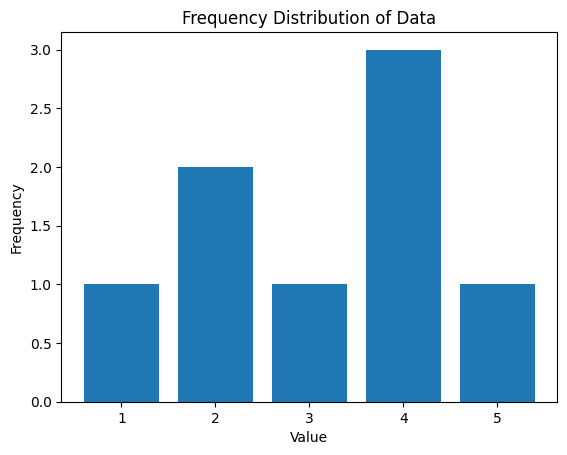
Pythonコードは、データセット data の度数分布を計算し、ヒストグラムとして表示する例です。

• Counter(data) は、データセット data 内の各値の出現回数を計算し、その結果を辞書のようなデータ構造で返します。このデータ構造には各値とその出現回数が含まれます。
• plt.bar(frequency.keys(), frequency.values()) は、度数分布をバー形式のヒストグラムとしてプロットします。frequency.keys() は度数分布の各値（値の一覧）を、frequency.values() はそれぞれの値の出現回数を提供します。
• plt.xlabel('Value') と plt.ylabel('Frequency') は、x軸とy軸のラベルを設定します。
• plt.title('Frequency Distribution of Data') は、ヒストグラムのタイトルを設定します。
• plt.show() は、ヒストグラムを表示します。

このコードは、データセット内の値の度数分布を計算し、その結果をヒストグラムとして視覚化します。ヒストグラムを通じて、データセット内の値の分布と頻度を視覚的に理解できます。

分散と標準偏差

分散と標準偏差は統計学的な概念で、データのばらつきを評価するための指標です。

1. 分散（Variance）:
   • 分散は、データセット内の各データポイントが、その平均値からどれだけ離れているかを示す数値です。
   • この離れ具合を数値化するために、各データポイントと平均値の差を計算し、それを二乗してから、それらの二乗値の平均を取ります。
   • これにより、データのばらつきを表現し、平均値からの距離を二乗しているため、離れているデータポイントの影響が大きくなります。
2. 標準偏差（Standard Deviation）:
   • 標準偏差は、分散の平方根です。分散と同様、データセット内のデータポイントが平均値からどれだけ離れているかを示しますが、分散よりも直感的な指標です。
   • 分散はデータのばらつきを二乗してしまうため、そのままではデータの散らばりを直感的に理解しにくいことがあります。標準偏差はこの問題を解決し、データの散らばりをもとのデータ単位で表現します。

ビジネスの応用例

ビジネスの応用例として、製品の品質管理や販売データの分析が挙げられます。品質管理では、製品の寸法や品質評価のデータから、製品の品質がどれだけばらついているかを評価するのに分散や標準偏差が使われます。販売データの分析では、売上データの変動を理解するためにこれらの指標を活用します。

Pythonコード

import statistics
data = [2, 5, 9, 12, 13, 7, 10, 11, 12, 9, 6]
variance = statistics.variance(data)
std_dev = statistics.stdev(data)
print(variance, std_dev)

11.618181818181819 3.4085454109021076

Pythonコードは、与えられたデータセットの分散と標準偏差を計算しています。分散は約11.62で、標準偏差は約3.41です。これらの値は、データセット内のデータポイントが平均からどれだけ散らばっているかを示しています。

散布図

散布図は、2つの変数の関係を視覚的に表現するためのグラフです。

1. 散布図（Scatter Plot）:
   • 散布図は、2つの異なる変数（データのセット）の間の関係を理解するのに役立つグラフです。通常、横軸（x軸）に1つの変数を、縦軸（y軸）にもう一つの変数を配置します。
   • 各データポイントは、横軸の値と縦軸の値に基づいて、散布図上に点として表示されます。このような点の集まりが、2つの変数間のパターンや関係性を視覚的に示します。

ビジネスの応用例

散布図は、ビジネス分析や意思決定の多くの側面で使用されます。例えば、以下のようなケースで役立ちます。

• 製品の価格と売上の関係を調べるため：横軸に価格、縦軸に売上をプロットし、価格と売上の間のパターンを視覚的に把握します。
• 広告費とWebサイトの訪問者数の関係を確認するため：広告費を横軸に、訪問者数を縦軸にプロットし、広告費の変化が訪問者数にどのように影響するかを確認します。

Pythonコード

import matplotlib.pyplot as plt
x = [10, 20, 30, 40, 50]
y = [5, 15, 25, 35, 50]
plt.scatter(x, y)
plt.show()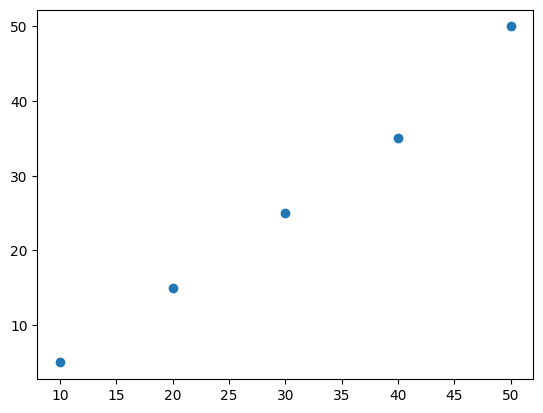

上記のPythonコードは、散布図を描くための簡単な例です。

• matplotlib.pyplot ライブラリを使用して、横軸（x）と縦軸（y）のデータをプロットし、plt.scatter() 関数を使用して点を表示します。
• plt.show() を呼び出すことで、実際のグラフが表示されます。

このコードは、xとyのデータを持つ散布図を描き、xとyの間の関係を可視化するのに役立ちます。

共分散と相関係数

共分散と相関係数は、2つの変数間の関係を評価する統計的な指標です。

1. 共分散（Covariance）:
   • 共分散は、2つの変数がどのように一緒に変動するかを示す値です。正の値は、1つの変数が増加するともう1つの変数も増加する傾向があることを示し、負の値は逆の傾向があることを示します。
2. 相関係数（Correlation Coefficient）:
   • 相関係数は、-1から1までの範囲の値を取り、2つの変数の線形的な関係の強さと方向を示す指標です。1に近い値は強い正の相関を示し、-1に近い値は強い負の相関を示します。0は相関がないことを示します。

ビジネスの応用例

共分散と相関係数は、ビジネス分析においてとても重要です。

• 製品の価格と売上の関係性を理解する：価格と売上データの共分散または相関係数を計算し、価格変動が売上にどのように影響するかを評価します。
• 広告費と収益の関係性を評価する：広告費と収益データの共分散または相関係数を計算し、広告費の変動が収益にどの程度影響を与えているかを把握します。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt

# ランダムデータの生成
np.random.seed(0)
x = 2.5 * np.random.randn(100) + 1.5   # Array of 100 values with mean = 1.5, stddev = 2.5
res = 0.5 * np.random.randn(100)       # Generate 100 residual terms
y = 2 + 0.3 * x + res                  # Actual values of Y

# 共分散と相関係数の計算
covariance = np.cov(x, y)[0, 1]
correlation = np.corrcoef(x, y)[0, 1]

# 散布図の作成
plt.figure(figsize=(8, 6))
plt.scatter(x, y, alpha=0.6, edgecolors="w", linewidth=0.5)
plt.title('Scatter plot with Covariance and Correlation')
plt.xlabel('X')
plt.ylabel('Y')
plt.text(0.5, 8, f'Covariance = {covariance:.2f}', fontsize=10, bbox=dict(facecolor='yellow', alpha=0.5))
plt.text(0.5, 7, f'Correlation = {correlation:.2f}', fontsize=10, bbox=dict(facecolor='lightgreen', alpha=0.5))
plt.show()

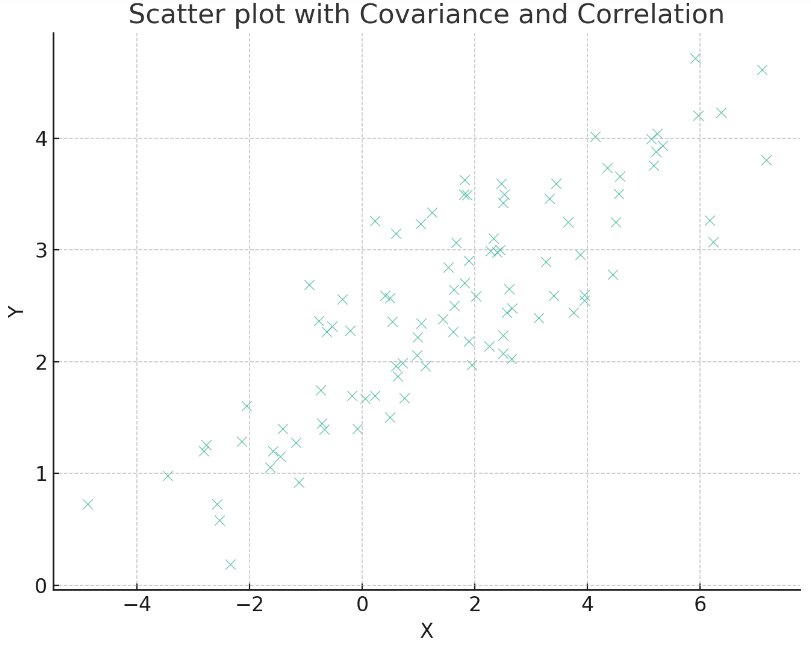
上記の散布図には、生成されたランダムデータセットがプロットされています。また、計算された共分散と相関係数がグラフ上に表示されています。

移動平均

移動平均は、時系列データの変動を平滑化するための手法です。

1. 移動平均（Moving Average）:
   • 移動平均は、一連のデータポイントに対して、一定の期間ごとの平均値を計算する手法です。
   • 時系列データはしばしばランダムな変動が含まれ、トレンドやパターンを見つけることが難しいことがあります。移動平均は、このようなランダムな変動を平滑化し、データ内のトレンドやパターンをより明確に見るのに役立ちます。

ビジネスの応用例

移動平均は、ビジネス分析や予測のさまざまな側面で使用されます。

• 株価の分析：株価チャートに移動平均線を描き、株価のトレンドを確認しやすくします。例えば、50日移動平均や200日移動平均などが一般的です。
• 売上データのトレンド分析：月ごとの売上データに移動平均を適用することで、季節的な変動やトレンドを特定し、将来の売上を予測するのに役立ちます。

Pythonコード

import matplotlib.pyplot as plt
def moving_average(data, window_size):
    return [sum(data[i:i+window_size])/window_size for i in range(len(data) - window_size + 1)]
data = [2, 5, 9, 12, 13, 7, 10, 11, 12, 9, 6]
window_size = 3
ma_data = moving_average(data, window_size)
# Create a plot
plt.figure(figsize=(8, 6))
plt.plot(data, label='Original Data')
plt.plot(range(window_size - 1, len(data)), ma_data, label=f'Moving Average (window_size={window_size})')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Moving Average of Data')
plt.legend()
plt.grid(True)
plt.show()

[5.333333333333333, 8.666666666666666, 11.333333333333334, 10.666666666666666, 10.0, 9.333333333333334, 11.0, 10.666666666666666, 9.0]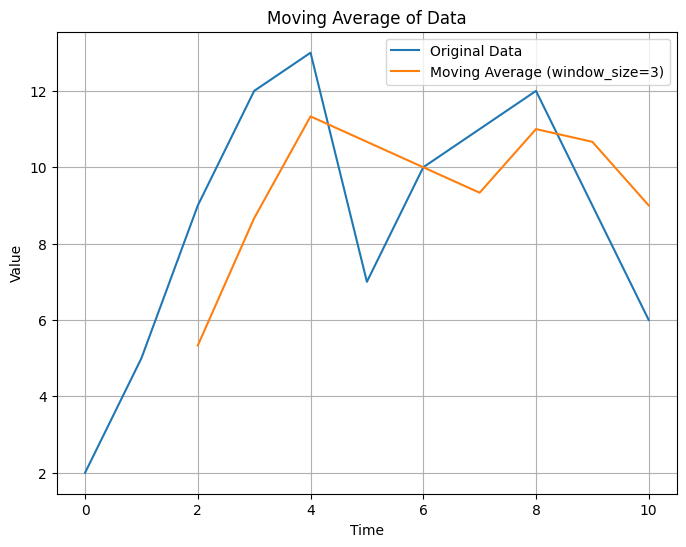

• Pythonコードは、指定したウィンドウサイズ（window_size）を使ってデータの移動平均を計算し、元のデータと移動平均値の両方を同じグラフ上にプロットする例です。
• moving_average 関数は、データ内の各ウィンドウにおける平均値を計算します。ウィンドウはデータ内をスライドして移動し、期間ごとの平均値を求めます。
• グラフは元のデータと移動平均値を比較し、データ内の変動を平滑化した結果を視覚化します。
• 与えられたデータセットとウィンドウサイズに基づいて、移動平均が計算されます。
• 移動平均の値 [5.33, 8.67, 11.33, 10.67, 10.0, 9.33, 11.0, 10.67, 9.0] は、ウィンドウサイズが3の場合の各期間ごとの平均値です。
• これらの平均値は、元のデータと一緒にグラフにプロットされ、データの変動のトレンドを視覚的に示しています。

回帰直線

回帰直線は、データの散布図において、2つの変数間の関係を最もよく表現する直線です。

1. 回帰直線（Regression Line）:
   • 回帰直線は、散布図上のデータポイントに合った直線で、2つの変数間の関係を要約したものです。この直線は、データポイントの中心的なトレンドやパターンを示します。
   • 回帰直線は通常、単回帰（1つの説明変数が目的変数に影響を与える場合）または重回帰（複数の説明変数が目的変数に影響を与える場合）の分析に使用されます。

ビジネスの応用例

回帰直線は、ビジネス分析と予測の多くの側面で使用されます。

• 価格設定戦略：製品の価格と売上データから回帰直線を計算し、価格と売上の関係を理解し、適切な価格設定戦略を立てるのに役立ちます。
• 広告費と収益：広告費と収益データから回帰直線を求め、広告費の変動が収益にどの程度影響を与えるかを評価します。

Pythonコード

from scipy.stats import linregress
x = [10, 20, 30, 40, 50]
y = [5, 15, 25, 35, 50]
slope, intercept, _, _, _ = linregress(x, y)
regression_line = [slope*xi + intercept for xi in x]
plt.scatter(x, y)
plt.plot(x, regression_line, color="red")
plt.show()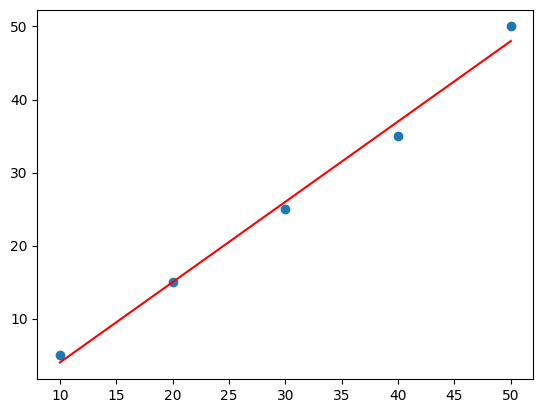

Pythonコードは、scipy.stats ライブラリの linregress 関数を使用して、与えられたデータポイントに対する回帰直線を計算し、それをグラフ上に表示する例です。

• linregress 関数は、与えられたデータに対する回帰直線の傾き（slope）、切片（intercept）などの統計的な情報を提供します。
• 散布図上にデータポイントを表示し、回帰直線（赤い直線）を描画して、データのパターンと回帰直線を比較できるようにしています。

このコードを実行することで、データの散布図に対する回帰直線を見ることができ、2つの変数間の関係を視覚的に理解できます。

微分の変化率

微分の変化率は、関数のある点における変化率を示すもので、その点における関数の勾配（傾き）として表現されます。

1. 微分の変化率（Derivative）:
   • 微分は、数学的な概念で、ある関数における変化の速さや傾きを表します。特定の点における微分は、その点における接線の傾きを示します。接線は、関数のグラフとその点で接する直線です。
   • 微分の変化率は、ある点から微小な変化が発生した場合に、関数の値がどれだけ変化するかを示します。変化率が正の場合、関数の値は増加します。変化率が負の場合、関数の値は減少します。

ビジネスの応用例

微分の概念は、ビジネス分析において以下のような応用があります。

• 成長率の評価：製品の生産量や売上データなどの時系列データに対して微分を適用することで、各期間における成長率や減少率を計算できます。これにより、製品の成長の速さや減少の程度を把握できます。
• 最適化：最大利益を追求するために、収益関数やコスト関数の微分を使用して、最適な戦略を見つけることがあります。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 100)
y = x**2
dy = np.gradient(y, x)
# Create a plot
plt.figure(figsize=(8, 6))
plt.plot(x, dy, label='Gradient of y')
plt.xlabel('x')
plt.ylabel('Gradient')
plt.title('Gradient of y = x^2')
plt.legend()
plt.grid(True)
plt.show()

[ 0.1010101   0.2020202   0.4040404   0.60606061  0.80808081  1.01010101
  1.21212121  1.41414141  1.61616162  1.81818182  2.02020202  2.22222222
  2.42424242  2.62626263  2.82828283  3.03030303  3.23232323  3.43434343
  3.63636364  3.83838384  4.04040404  4.24242424  4.44444444  4.64646465
  4.84848485  5.05050505  5.25252525  5.45454545  5.65656566  5.85858586
  6.06060606  6.26262626  6.46464646  6.66666667  6.86868687  7.07070707
  7.27272727  7.47474747  7.67676768  7.87878788  8.08080808  8.28282828
  8.48484848  8.68686869  8.88888889  9.09090909  9.29292929  9.49494949
  9.6969697   9.8989899  10.1010101  10.3030303  10.50505051 10.70707071
 10.90909091 11.11111111 11.31313131 11.51515152 11.71717172 11.91919192
 12.12121212 12.32323232 12.52525253 12.72727273 12.92929293 13.13131313
 13.33333333 13.53535354 13.73737374 13.93939394 14.14141414 14.34343434
 14.54545455 14.74747475 14.94949495 15.15151515 15.35353535 15.55555556
 15.75757576 15.95959596 16.16161616 16.36363636 16.56565657 16.76767677
 16.96969697 17.17171717 17.37373737 17.57575758 17.77777778 17.97979798
 18.18181818 18.38383838 18.58585859 18.78787879 18.98989899 19.19191919
 19.39393939 19.5959596  19.7979798  19.8989899 ]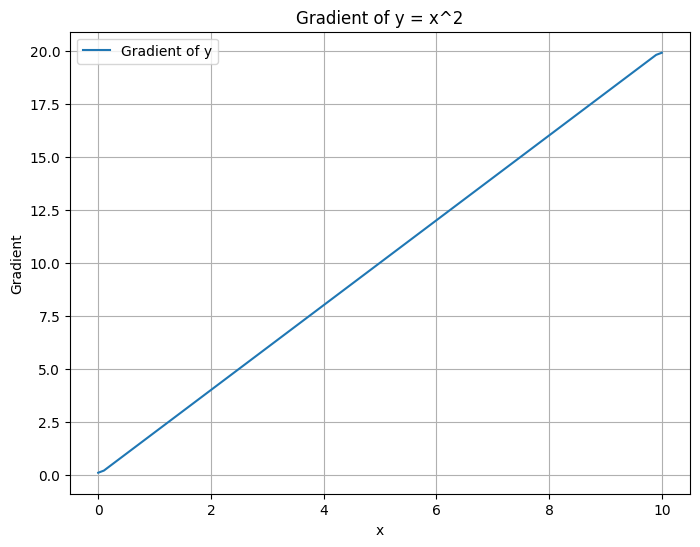

Pythonコードは、NumPyおよびMatplotlibライブラリを使用して、特定の関数 y = x^2 の微分の変化率を計算し、グラフ上にプロットする例です。

• np.linspace(0, 10, 100) を使用して、xの範囲を0から10まで100の等間隔の点で生成します。
• y = x^2 の関数を表すために y = x**2 を使用します。
• np.gradient() 関数を使用して、xに対するyの勾配（変化率）を計算します。
• グラフ上にxに対する勾配をプロットして、関数 y = x^2 の各点における変化率を可視化します。

このコードを実行することで、関数の微分による変化率がxの範囲内でどのように変化するかを理解できます。

微分係数

微分係数は、関数のある点での微分（導関数）の値を指します。これは、その点での関数の変化の速さを示す数値です。

1. 微分係数:
   • 微分係数は、関数の特定の点における変化率を表します。具体的には、その点における接線の傾きを示します。
   • 関数がある点で急峻に上昇している場合、微分係数は正の値となり、関数が下降している場合は負の値となります。
   • 微分係数がゼロの場合、関数はその点で水平です。

ビジネスの応用例

微分係数は、ビジネス分析において価値があります。

• 価格弾力性の評価：製品の価格変動が売上に与える影響を理解するために、価格の微小な変化に対する売上の変化率を知る必要があります。微分係数を使用して、価格弾力性を評価できます。

Pythonコード

from sympy import symbols, diff
x = symbols('x')
f = x**2
diff_coefficient = diff(f, x)

2*x

• Pythonコードは、Sympyライブラリを使用して、関数 f = x^2 の微分係数を計算する例です。
• symbols('x') を使用して、変数 x を宣言します。
• f = x**2 で関数を表します。
• diff(f, x) 関数を使用して、関数 f を変数 x に関して微分し、その微分係数を計算します。
• 結果として、微分係数 2*x が得られます。これは x の値に依存する関数で、その点での微分係数を示します。

このコードを実行することで、関数 f = x^2 の微分係数が 2*x であることがわかります。したがって、関数の各点における変化率は 2*x によって表されます。

微分する

「微分する」とは、与えられた関数を微分して新しい関数、つまり導関数（後述）を得る操作を指します。

1. 微分する:
   • 微分は、関数がある点での変化率を計算する操作です。特に、ある点での接線の傾きを求めることで、その点での関数の振る舞いを理解できます。
   • 関数を微分することにより、元の関数から導関数を得ることができます。導関数は、関数の各点における変化率を表す新しい関数です。
   • 微分にはさまざまなルールがあり、微分したい関数の形に応じて適用されます。

ビジネスの応用例

微分はビジネス分析や最適化の際にとても重要です。

• 最小値を見つける：コスト関数や収益関数など、ビジネス上の問題で最適な解を見つけるために微分を使用します。最小値（または最大値）は導関数がゼロになる点で見つけることができます。これは、例えば生産コストを最小化するための最適な生産数量を見つける際に役立ちます。

Pythonコード

from sympy import symbols, diff
x = symbols('x')
f = x**3 - 3*x**2 + 2*x
df = diff(f, x)
print(df)

3*x**2 - 6*x + 2

上記のPythonコードは、Sympyライブラリを使用して、関数 f = x^3 - 3*x^2 + 2*x の微分を計算し、その導関数を表示する例です。

• symbols('x') を使用して、変数 x を宣言します。
• f = x**3 - 3*x**2 + 2*x で関数を表します。
• diff(f, x) 関数を使用して、関数 f を変数 x に関して微分し、その導関数を計算します。
• 結果として、導関数 3*x**2 - 6*x + 2 が得られます。これは、元の関数の各点における変化率を表す導関数です。

このコードを実行することで、関数 f = x^3 - 3*x^2 + 2*x の導関数が 3*x**2 - 6*x + 2 であることがわかります。したがって、この導関数は元の関数の各点における変化率を表しています。

導関数とは

導関数とは、元の関数を微分して得られる新しい関数を指します。導関数は、元の関数がある点での変化率を表現し、その点での関数の振る舞いを理解するのに役立ちます。

1. 導関数:
   • 導関数は、与えられた関数を微分した結果得られる新しい関数です。導関数は、元の関数がある点での変化の速さを表します。
   • 導関数の値はその点における接線の傾きを示し、その点での関数の上昇または下降の速さを定量化します。

ビジネスの応用例

導関数はビジネス分析においてさまざまな応用があります。

• 需要予測モデルの最適化：製品の需要予測モデルの精度を向上させるために、コスト関数の導関数を使用してモデルのパラメータを調整することがあります。導関数を最小化することにより、モデルの予測精度を最適化できます。

Pythonコード

from sympy import symbols, diff
x = symbols('x')
f = x**2 - 4*x + 4
df = diff(f, x)

2*x - 4

上記のPythonコードは、Sympyライブラリを使用して、関数 f = x^2 - 4*x + 4 の導関数を計算し、その導関数を表示する例です。

• symbols('x') を使用して、変数 x を宣言します。
• f = x**2 - 4*x + 4 で関数を表します。
• diff(f, x) 関数を使用して、関数 f を変数 x に関して微分し、その導関数を計算します。
• 結果として、導関数 2*x - 4 が得られます。これは、元の関数の各点における変化率を表す導関数です。

このコードを実行することで、関数 f = x^2 - 4*x + 4 の導関数が 2*x - 4 であることがわかります。したがって、この導関数は元の関数の各点における変化率を示しています。

微分の公式

微分の公式は、特定の関数の形に対する微分操作の結果を表す数学的な公式です。異なる種類の関数に対する微分操作を簡略化し、効率的に計算するためのツールです。

• 微分の公式は、特定の関数形に対する微分操作を示す数式です。これにより、関数がどのように変化するかを簡単に計算できます。
• 例えば、\( ax^n \) 形式の関数の微分は、\( anx^{n-1} \) という公式になります。ここで、\( a \) は定数で、\( n \) は指数です。
• 他にも、三角関数、指数関数、対数関数などに対する微分公式が存在し、各関数の特性に合わせて微分を行う際に役立ちます。

ビジネスの応用例

微分の公式は、ビジネス分析において以下のような応用があります。

• コスト関数の最適化：製品の生産コストを表すコスト関数を最小化するために微分を使用する場合、微分の公式を活用してコスト関数の導関数を計算し、最小値を求めることができます。これにより、最適な生産数量や価格を決定できます。

Pythonコード

from sympy import symbols, diff
x = symbols('x')
f = 3*x**4 - 5*x**3 + 2*x**2
df = diff(f, x)

12*x**3 - 15*x**2 + 4*x

上記のPythonコードは、Sympyライブラリを使用して、関数 f = 3*x**4 - 5*x**3 + 2*x**2 の微分を計算し、その導関数を表示する例です。

• symbols('x') を使用して、変数 x を宣言します。
• f = 3*x**4 - 5*x**3 + 2*x**2 で関数を表します。
• diff(f, x) 関数を使用して、関数 f を変数 x に関して微分し、その導関数を計算します。
• 結果として、導関数 12*x**3 - 15*x**2 + 4*x が得られます。これは、元の関数の各点における変化率を表す導関数です。

このコードを実行することで、関数 f = 3*x**4 - 5*x**3 + 2*x**2 の導関数が 12*x**3 - 15*x**2 + 4*x であることがわかります

極小と極大

極小点と極大点は、関数の振る舞いにおける重要な特別な点を指します。

1. 極小点と極大点:
   • 極小点：関数がある点において、その近傍で最も小さい値を持つ点を極小点と呼びます。極小点では、関数がその点を中心に上昇から下降に転じます。
   • 極大点：関数がある点において、その近傍で最も大きい値を持つ点を極大点と呼びます。極大点では、関数がその点を中心に下降から上昇に転じます。

ビジネスの応用例

極小点と極大点はビジネス分析において以下のような応用があります。

• 最適化：製品のコスト、売上、利益などの関数を最適化するために、関数の極小点や極大点を求めることがあります。例えば、最適な生産数量や価格を見つけるために使用できます。

Pythonコード

from sympy import symbols, diff, solve
x = symbols('x')
f = x**3 - 3*x**2 + 2*x
df = diff(f, x)
critical_points = solve(df, x)

[1 - sqrt(3)/3, sqrt(3)/3 + 1]

上記のPythonコードは、Sympyライブラリを使用して、関数 f = x**3 - 3*x**2 + 2*x の極小点と極大点を計算する例です。

• symbols('x') を使用して、変数 x を宣言します。
• f = x**3 - 3*x**2 + 2*x で関数を表します。
• diff(f, x) 関数を使用して、関数 f を変数 x に関して微分し、その導関数を計算します。
• solve(df, x) を使用して、導関数がゼロとなる点を見つけます。これらの点が関数の極小点と極大点です。
• 結果として、極小点が [1 - sqrt(3)/3, sqrt(3)/3 + 1] として得られます。

このコードを実行することで、関数 f = x**3 - 3*x**2 + 2*x の極小点と極大点が求められます。これらの点は、関数が最小または最大となる場所を示します。

積分とは

積分は、数学的な手法の一つで、関数の下での面積や空間内の体積を計算するために使用されます。不定積分と定積分の2つの主要な種類があります。

• 積分は、関数が与えられた領域でどれだけの面積を占めるか、または空間内でどれだけの体積を持つかを計算する数学的な操作です。
• 不定積分（indefinite integral）は、関数の原始関数（antiderivative）を求める操作で、導関数が与えられた関数になるような関数を見つけることを意味します。不定積分は通常 \( \int \) と表記されます。
• 定積分（definite integral）は、特定の区間で関数の下での面積や体積を計算するために使用されます。定積分は通常 \(\int_a^b\) と表記され、区間 \([a, b]\) 内での積分値を示します。

ビジネスの応用例

積分はビジネス分析において以下のような応用があります。

• 生産量の計算：製品の生産速度が時間に対してどのように変化するかを知っている場合、積分を使用してある時間間隔内での生産量を計算できます。これにより、製品の在庫管理や生産計画を最適化できます。

Pythonコード

import numpy as np
from scipy.integrate import quad
func = lambda x: x**2
result, _ = quad(func, 0, 1)

0.33333333333333337

上記のPythonコードは、Scipyライブラリを使用して、関数 \(f(x) = x^2\) の不定積分を計算し、区間 \([0, 1]\) での定積分値を示す例です。

• quad 関数を使用して不定積分を計算し、結果として積分値が得られます。
• 結果として、積分値は約 \(0.333\) です。

このコードを実行することで、関数 \(f(x) = x^2\) の不定積分と定積分が計算され、区間 \([0, 1]\) での積分値が示されます。この値は、関数 \(f(x)\) の区間 \([0, 1]\) 内での面積を表します。

積分する

積分は、関数の特定の区間における面積を計算したり、関数の原始関数（後述）を求めたりする数学的操作を指します。

• 積分するとは、与えられた関数をある区間で積分することです。これにより、関数のグラフの特定の区間での面積や、その関数に関連付けられた原始関数を求めることができます。

ビジネスの応用例

• エネルギー消費の計算：エネルギー消費の時間変化がわかっている場合、その期間内の総エネルギー消費を計算するために積分を使用できます。たとえば、特定の期間における総エネルギー消費量を求めることができます。これは、エネルギー効率の改善や予算の立案に役立ちます。

Pythonコード

from scipy.integrate import quad
func = lambda x: 3*x**2 + 2*x
result, _ = quad(func, 0, 2)
print("積分結果:", result)

積分結果: 12.0

上記のPythonコードは、Scipyライブラリを使用して、関数 \(f(x) = 3x^2 + 2x\) の不定積分を計算し、区間 \([0, 2]\) での定積分値を求める例です。

• quad 関数を使用して、関数 func の積分を計算し、結果として積分値が result に格納されます。
• 結果として、積分値は特定の区間 \([0, 2]\) 内での関数の面積を表します。この場合、関数 \(f(x)\) の区間 \([0, 2]\) での面積が計算されます。

このコードを実行することで、関数 \(f(x) = 3x^2 + 2x\) の区間 \([0, 2]\) での積分値が計算され、その区間での面積が示されます。

定積分・不定積分

定積分と不定積分は、積分の2つの主要な種類であり、それぞれ異なる目的に使用されます。

• 定積分は、関数の特定の区間における面積を計算するための数学的な操作です。特定の範囲内で関数がどれだけの面積を占めているかを示します。数学的には、\(\int_a^b f(x) \, dx\) と表記され、関数 \(f(x)\) を範囲 \([a, b]\) で積分することを示します。
• 不定積分は、関数の原始関数（antiderivative）を求める操作です。不定積分を行うと、導関数が与えられた関数になるような関数を見つけることができます。不定積分は通常、\\(\int f(x) \, dx\\) と表記されます。

ビジネスの応用例

• 定積分：商品の販売速度の時間変化が分かっている場合、特定の期間での総販売数を計算するために定積分を使用できます。例えば、特定の月の総売上を求めるために使用できます。
• 不定積分：商品の販売速度の関数を知っている場合、販売速度から販売数を計算するために不定積分を使用できます。これにより、時間の経過に伴う販売数の変化を予測できます。

Pythonコード

from scipy.integrate import quad
from scipy.integrate import quad, solve_ivp

# 定積分
func = lambda x: 2*x + 1
result, _ = quad(func, 0, 3)
print(result)

# 不定積分（原始関数を近似的に求める）
def model(t, y): return 2*t + 1
sol = solve_ivp(model, [0, 3], [0])
print(sol)

12.0
  message: The solver successfully reached the end of the integration interval.
  success: True
   status: 0
        t: [ 0.000e+00  1.000e-04  1.100e-03  1.110e-02  1.111e-01
             1.111e+00  3.000e+00]
        y: [[ 0.000e+00  1.000e-04  1.101e-03  1.122e-02  1.234e-01
              2.346e+00  1.200e+01]]
      sol: None
 t_events: None
 y_events: None
     nfev: 38
     njev: 0
      nlu: 0

上記のPythonコードは、Scipyライブラリを使用して、定積分と不定積分の計算例です。

• 定積分の例では、関数 \(f(x) = 2x + 1\) を範囲 \([0, 3]\) で積分し、結果として面積が result に格納されます。この場合、結果は12.0です。
• 不定積分の例では、関数 \(f(t) = 2t + 1\) の原始関数を近似的に求めるために solve_ivp 関数を使用しています。これにより、関数 \(f(t)\) の原始関数が得られ、時間に対する変化を示します。

このコードを実行することで、定積分と不定積分の基本的な概念が示され、ビジネスにおける応用例が説明されています。

原始関数

• 原始関数は、ある関数 \(f(x)\) を不定積分することによって得られる関数です。不定積分を行うことで、元の関数に対して微分操作を逆にしたような操作を行います。
• 数学的には、\(F(x)\) が関数 \(f(x)\) の原始関数であるとき、次のように表現されます。\[F(x) = \int f(x) \, dx\]

ビジネスの応用例

原始関数は、コスト関数の変化を知っている場合に、ある期間の総コストを求めるために使用されます。たとえば、特定の生産プロセスのコスト関数が与えられた場合、原始関数を使用して生産の総コストを計算できます。

Pythonコード

from sympy import symbols, integrate
x = symbols('x')
func = 2*x + 1
primitive_func = integrate(func, x)
print(primitive_func)

x**2 + x

上記のPythonコードは、SymPyライブラリを使用して、関数 \(f(x) = 2x + 1\) の原始関数を計算し、その結果を示しています。

• integrate 関数を使用して、関数 func の不定積分を計算し、結果として原始関数 primitive_func が得られます。この場合、原始関数は \(x^2 + x\) です。

このコードを実行することで、関数 \(f(x) = 2x + 1\) の原始関数が計算され、それがどのように得られるかが示されます。原始関数は、不定積分の結果として得られるものであり、微分操作を逆にできることが特徴です。

積分定数Cとは

積分定数Cは、不定積分の結果に追加される定数です。

1. 積分定数C: 積分定数Cは、不定積分を計算した際に現れる定数です。不定積分は、関数を積分する過程で特定の区間を指定せずに行われるため、不確定性が残ります。そのため、不定積分の結果には積分定数Cが含まれ、具体的な値が指定されていないため、Cは任意の実数を取ることができます。

ビジネスの応用例

積分定数Cは、物理学、工学、経済学などのさまざまな分野で使用されます。特に初期条件や境界条件を満たすための調整要因として役立ちます。たとえば、物理学の運動方程式を解く際に、初期速度や初期位置を表す積分定数Cが必要です。経済学の場合、積分定数Cは初期資本や初期需要などを示すのに使われることがあります。

Pythonコード

from sympy import symbols, integrate
x, C = symbols('x C')
primitive_func = integrate(2*x, x) + C
print(primitive_func)

C + x**2

上記のPythonコードは、積分定数Cが不定積分の結果に含まれることを示す例です。具体的には、不定積分を計算する際にCを追加しています。このCは、不定積分の結果において、特定の初期条件や境界条件に応じて調整される値であることを示しています。

積分定数Cは、数学的な計算や物理的なモデリングにおいて、問題の特性や初期条件に合わせて調整される重要な要素です。

微分・積分

微分と積分は、数学の基本的な概念です。

1. 微分: 微分は、関数の局所的な変化率を調査する手法です。具体的には、関数の各点での勾配（傾き）を計算し、その点における関数の振る舞いを理解します。微分を用いることで、関数がどのように急峻に上昇または下降しているか、極小値や極大値を見つけることができます。
2. 積分: 積分は、関数の区間における面積や、関数の原始関数を求める手法です。特定の区間で関数が囲む面積を計算できるため、積分は領域の面積や累積量を求めるのに役立ちます。また、微分の逆操作としても知られており、微分によって得られた関数を元の関数に戻すことができます。

ビジネスの応用例

微分と積分は、ビジネスにおいても広く使用されます。たとえば、製品の販売速度を微分により求めることで、ある瞬間における販売の速さを知ることができます。そして、この結果を積分することで、ある期間の総販売量を計算できます。このように、微分と積分は販売データの分析や需要予測などのビジネスにおける重要なツールとして使用されます。

Pythonコード

from sympy import symbols, diff, integrate
x = symbols('x')
func = x**2
diff_func = diff(func, x)
integrated_func = integrate(diff_func, x)
print(integrated_func)

x**2

上記のPythonコードは、関数 x**2 を微分してから積分する例です。まず、diff(func, x) を使用して関数の微分を計算し、次にintegrate(diff_func, x) を使用して微分の逆操作である積分を行います。最終的に、元の関数 x**2 が再び得られます。

微分と積分は数学と科学の基盤であり、多くの分野で応用されています。ビジネス分野では、データの解析や最適化などに役立つ重要な数学的ツールとして利用されています。

微分と積分の関係

• 微分と積分は、関数に対する2つの基本的な操作です。微分は関数の導関数（変化率）を求め、積分は関数の不定積分（面積または原始関数）を求めます。
• これら2つの操作は逆の関係にあります。つまり、関数を微分して導関数を得た後、その導関数を積分すると、元の関数が得られます（定数を除く）。

ビジネスの応用例

微分を使用して製品の販売速度を求めた場合、その結果を積分することで、ある期間の総販売量を計算できます。たとえば、日々の販売速度から月間の総販売量を計算できます。

Pythonコード

from sympy import symbols, diff, integrate
x = symbols('x')
func = x**2
diff_func = diff(func, x)
integrated_func = integrate(diff_func, x)
print(integrated_func)

x**2

上記のPythonコードは、SymPyライブラリを使用して、関数 \(f(x) = x^2\) を微分してから積分する例です。

• まず、関数 func を微分し、その結果を diff_func に格納します。この場合、導関数は \(2x\) です。
• 次に、導関数 diff_func を積分し、その結果を integrated_func に格納します。この積分により、元の関数 \(x^2\) が復元されます。

このコードを実行することで、微分と積分の関係が示され、微分した後に積分を行うことで元の関数を再構築できることがわかります。

期待値と分散

期待値と分散は統計学と確率論の基本的な概念です。

1. 期待値: 期待値は、確率変数の平均値を示します。確率変数は、ランダムな値を取る変数であり、その平均値はその確率変数が取り得る値の重みつき平均です。期待値は、確率分布を考慮して、各値をその確率で重みづけた平均です。例えば、サイコロを振る場合、1から6の値が等しい確率で出る場合、期待値は (1+2+3+4+5+6)/6 = 3.5 となります。
2. 分散: 分散は、確率変数がどれだけばらついているかを示す尺度です。分散が小さいほど、確率変数の値は平均値に近く、分散が大きいほど、値は平均から離れた範囲に分布します。分散は、各値と平均値の差の二乗を計算し、その平均を取ることで求められます。分散がゼロの場合、確率変数は一定の値しか取らないことを示し、分散が大きい場合、値は広い範囲に分布しています。

ビジネスの応用例

期待値と分散は、ビジネスにおいても重要な役割を果たします。商品の売上予測を例に取ると、過去の売上データの期待値を計算することで、平均的な売上を把握できます。また、分散を調べることで、売上のばらつきやリスクを評価できます。これにより、将来の売上の予測と、その予測の信頼性を評価するのに役立ちます。

Pythonコード

import numpy as np
data = [10, 20, 30, 40, 50]
mean = np.mean(data)
variance = np.var(data)
print(variance)

200.0

上記のPythonコードは、与えられたデータセットの分散を計算する例です。データセット [10, 20, 30, 40, 50] の分散は 200.0 です。この値は、データポイントが平均値からどれだけばらついているかを示しています。

期待値と分散は、統計的な分析や意思決定において、データの特性やリスクの評価に役立つ重要な統計量です。

2つの確率変数

確率変数とは、ランダムな結果を持つ変数です。2つの確率変数がある場合、それぞれの確率変数が異なる出来事や値に関連している可能性があります。これらの確率変数の関係性や相互作用を調査することは、データ分析や統計学の重要な要素です。

ビジネスの応用例

ビジネスでは、2つの異なる製品の売上データを分析することがよくあります。たとえば、AとBという2つの製品がある場合、Aの売上が増加すると、Bの売上にどのような影響があるかを調査します。このような分析は、戦略的な意思決定に役立ちます。例えば、AとBが競合関係にある場合、Aの売上が上がるとBの売上が減少する可能性があるかもしれません。逆に、AとBが補完関係にある場合、Aの売上増加がBの売上増加につながるかもしれません。したがって、2つの確率変数の関係を理解することは、製品戦略や市場戦略においてとても重要です。

2つの確率変数の相互作用を調査するために、統計モデルやデータ分析手法を使用することが一般的です。これにより、ビジネスの意思決定者は、異なる要因間の関係性を理解し、適切な戦略を策定するのに役立つ情報を得ることができます。

Pythonコード

# No specific code for this, as it's a general concept.

独立と共分散

2つの確率変数が独立の場合、一方の変数の変化がもう一方の変数の変化に影響を与えません。共分散は、2つの変数の関係性の強さを示します。

1. 独立性: 2つの確率変数が独立している場合、一方の変数の値が変化しても、もう一方の変数には影響を与えません。言い換えれば、一方の変数の値がわかっても、もう一方の変数の予測に役立つ情報は得られません。例えば、コインを2回投げる場合、1回目の結果が表か裏かは、2回目の結果に影響を与えません。これらの事象は独立しています。
2. 共分散: 共分散は、2つの変数の関係性や一緒に変動する度合いを示す統計的な尺度です。正の共分散は、2つの変数が一緒に変動することを示し、負の共分散は、1つの変数が増加するともう一方が減少することを示します。共分散の絶対値が大きいほど、変数間の関係が強いことを示し、絶対値が小さいほど関係が弱いことを示します。ただし、共分散の単位は変数の単位の積であり、単位に依存するため、絶対値自体には意味がありません。

ビジネスの応用例

ビジネスの分野では、2つの変数（例: 製品Aの売上と製品Bの売上）の共分散を計算して、これらの変数の関係性を評価します。共分散が正の場合、製品Aの売上が増加すると、製品Bの売上も増加する可能性があります。逆に、共分散が負の場合、製品Aの売上増加が製品Bの売上減少につながる可能性があります。共分散を計算することで、製品戦略や販売戦略を最適化する際に、2つの変数間の関係を理解し、意思決定をサポートできます。

Pythonコード

import numpy as np
sales_A = [10, 20, 30, 40, 50]
sales_B = [5, 15, 25, 35, 45]
covariance = np.cov(sales_A, sales_B)[0, 1]
print(covariance)

250.0

上記のPythonコードは、2つの製品の売上データから共分散を計算する例です。np.cov() 関数を使用して、sales_A と sales_B の共分散を計算し、結果は 250.0 です。この値は、売上データ間の関係性を示します。

共分散とグラフの関係

共分散は、2つの変数間の関係性を示す統計的な尺度です。共分散が正の場合、2つの変数は同じ方向に動く傾向があり、つまり一方の変数が増加するともう一方も増加する傾向があります。逆に、共分散が負の場合、2つの変数は逆の方向に動く傾向があり、一方の変数が増加するともう一方は減少する傾向があります。

ビジネスの応用例

売上と広告費の共分散をグラフで表示することで、広告費の増加が売上にどのような影響を与えるかを視覚的に理解できます。具体的には、広告費を横軸に、売上を縦軸にプロットした散布図を作成します。この散布図において、広告費と売上が正の共分散を持つ場合、散布図上の点は一般的に右上がりの傾向を示し、つまり広告費が増加すると売上も増加する傾向があります。逆に、共分散が負の場合、散布図上の点は左下がりの傾向を示し、広告費が増加すると売上が減少する傾向があります。

Pythonコード

import matplotlib.pyplot as plt
ad_costs = [100, 200, 300, 400, 500]
sales = [1100, 2200, 3300, 4400, 5500]
plt.scatter(ad_costs, sales)
plt.xlabel("Ad Costs")
plt.ylabel("Sales")
plt.title("Relationship between Ad Costs and Sales")
plt.show()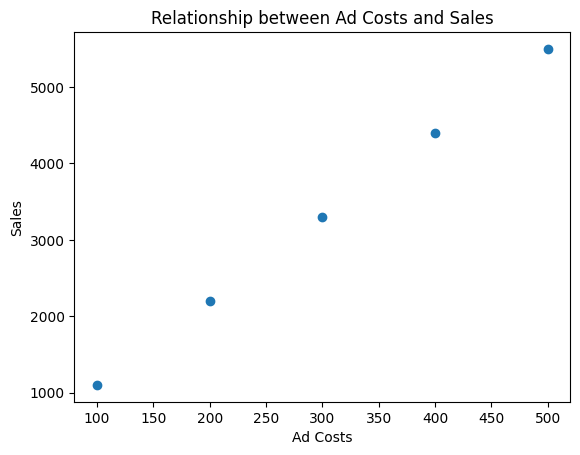

上記のPythonコードは、広告費と売上データを使用して散布図を作成する例です。plt.scatter(ad_costs, sales) の行で、広告費を横軸に、売上を縦軸にプロットし、点として表示します。この散布図を通じて、広告費と売上の関係性が直感的に理解できます。

共分散と散布図を組み合わせることで、2つの変数間の関係性を視覚的に把握し、ビジネス上の意思決定に役立てることができます。

相関係数と決定係数

相関係数は、2つの変数の関係性の強さと方向を示し、決定係数は、一方の変数の変動がもう一方の変数によってどれだけ説明されるかを示します。

1. 相関係数: 相関係数は、2つの変数間の関係性の強さと方向を示す統計的な尺度です。相関係数は、-1から+1の範囲の値を取ります。具体的には、
   • 相関係数が-1の場合：完全な負の線形関係があります。一方の変数が増加すれば、もう一方は減少します。
   • 相関係数が0の場合：変数間に線形関係はありません。変数間の関係性は存在しないか、非線形の場合です。
2. 決定係数: 決定係数（R^2）は、一方の変数の変動がもう一方の変数によってどれだけ説明されるかを示す指標です。R^2は0から1の範囲の値を取り、
   • R^2が0に近い場合：変数間の関係性が弱いか、ほとんど説明できていないことを示します。
   • R^2が1に近い場合：変数間の関係性が強く、一方の変数がもう一方をよく説明していることを示します。

ビジネスの応用例

製品の価格と売上の間の相関係数を計算することで、価格変動が売上に与える影響の強さを評価できます。相関係数が正の場合、価格と売上が正の関係にあり、価格上昇が売上増加に寄与する可能性があります。決定係数は、この関係性の強さを示し、価格変動が売上変動のどれだけを説明できるかを示します。高い決定係数は、価格が売上に強く影響を与えることを示し、ビジネス戦略の立案や価格戦略の決定に役立ちます。

Pythonコード

import numpy as np
prices = [10, 20, 30, 40, 50]
sales = [50, 45, 40, 35, 30]
correlation_coefficient = np.corrcoef(prices, sales)[0, 1]
determination_coefficient = correlation_coefficient**2
print(determination_coefficient)

1.0

上記のPythonコードは、価格と売上データから相関係数を計算し、それを用いて決定係数を計算する例です。np.corrcoef() 関数を使用して相関係数を計算し、それを2乗して決定係数を得ています。この例では、相関係数が1.0であるため、価格と売上の間に完全な正の関係があり、決定係数も1.0となります。

直線の近似

直線の近似は、与えられたデータセットに最も合致する直線を見つける作業を指します。この直線は、データポイントをできるだけ近似するように配置され、通常は最小二乗法などの統計的手法を使用して見つけられます。最小二乗法は、データポイントと直線の間の距離（誤差）を最小化する直線を見つける方法です。この直線を通じて、データの傾向やパターンを要約し、将来の予測や分析に役立ちます。

ビジネスの応用例

ビジネスの分野では、過去のデータ（例: 過去の売上データ）を使用して、将来を予測するための直線の近似が一般的です。この近似直線を用いることで、過去の傾向やパターンをもとに将来の売上を予測できます。たとえば、売上データを直線に近似することで、ある期間内の売上の増加率やトレンドを把握し、新しい製品の需要を予測したり、在庫管理を最適化したりするのに役立ちます。

Pythonコード

from scipy.stats import linregress
x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]
slope, intercept, _, _, _ = linregress(x, y)
print(slope)

2.0

上記のPythonコードは、データセットを使用して直線の近似を行う例です。linregress() 関数を使用して、データポイント x と y をもとに最適な直線を近似し、その直線の傾き（slope）を計算しています。この例では、データセットが (1, 2), (2, 4), (3, 6), (4, 8), (5, 10) であるため、傾きは2.0となります。この傾きは、データポイントがy=2xという直線に近似されたことを示しています。

直線の近似は、データ分析や予測モデリングにおいて基本的な要素であり、ビジネスにおいても幅広く利用されています。

回帰分析

回帰分析は、変数間の関係を統計的にモデル化するための手法です。この手法は、一つまたは複数の入力変数（独立変数または説明変数）から出力変数（従属変数または目的変数）の値を予測するのに使用されます。回帰分析は、変数間の関係を理解し、未来の値を予測するための有用なツールです。代表的な回帰分析の種類には、単回帰分析（1つの説明変数を使用）、重回帰分析（複数の説明変数を使用）、多項式回帰分析（高次の多項式を使用）などがあります。

ビジネスの応用例

ビジネスの分野では、回帰分析がさまざまな場面で利用されます。例えば、製品の価格と売上の関係を分析する際、回帰分析を使用して特定の価格設定での売上を予測できます。また、広告費と売上、商品の特性と需要、顧客の属性と購買行動など、さまざまな要因に関連するビジネスの課題に対しても回帰分析が適用されます。これにより、戦略立案や意思決定プロセスをデータに基づいてサポートするのに役立ちます。

Pythonコード

import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 4, 5, 4, 5])
model = LinearRegression().fit(X, y)
predicted_y = model.predict(X)
print(predicted_y)

[2.8 3.4 4.  4.6 5.2]

上記のPythonコードは、単回帰分析の例です。X が価格（説明変数）、y が売上（目的変数）のデータを表します。LinearRegression() モデルを使用して、データに最適な直線モデルを適合させ、そのモデルを使用して新しい価格に対する売上を予測しています。この例では、価格が [1, 2, 3, 4, 5] であり、それに対する予測売上が [2.8, 3.4, 4.0, 4.6, 5.2] となります。

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# Given data
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 4, 5, 4, 5])

# Linear regression
model = LinearRegression().fit(X, y)
predicted_y = model.predict(X)

# Plotting
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Actual Data')
plt.plot(X, predicted_y, color='red', label='Linear Regression')
plt.title('Linear Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

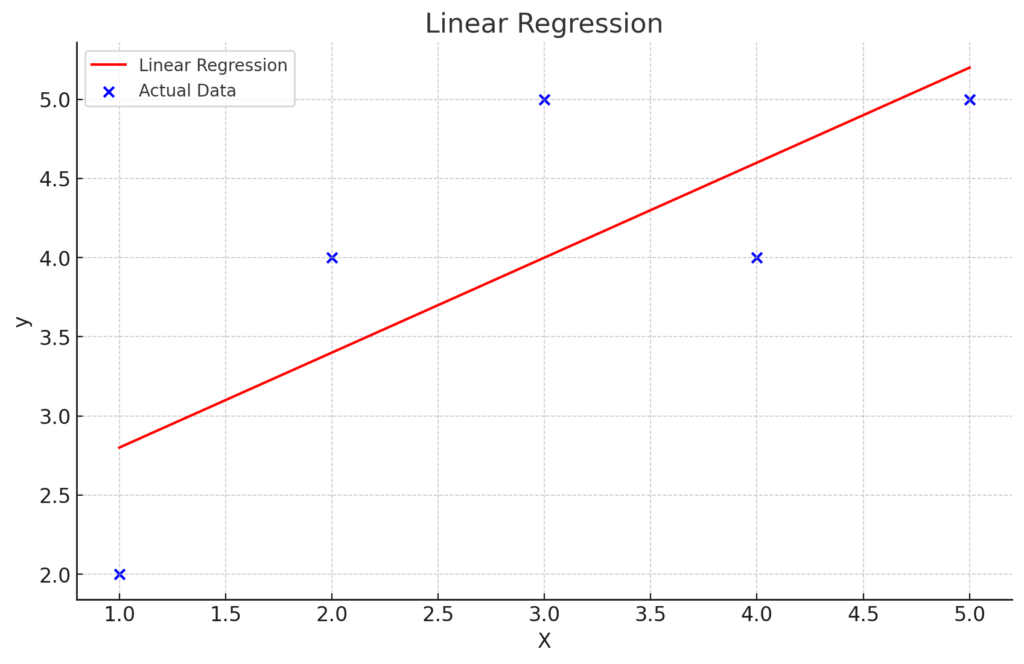
青い点が実際のデータ、赤い線が線形回帰モデルによって予測されたデータを表しています。これにより、価格と売上の関係が数値的にモデル化され、価格設定の意思決定に役立つ情報が得られます。

回帰分析は、データ駆動型の意思決定においてとても有用であり、ビジネス戦略の最適化やリスク評価に貢献します。

最小二乗法

最小二乗法は、線形回帰の背後にある主要な手法の1つです。最小二乗法は、実際のデータ点と回帰直線との差（誤差）の二乗和を最小にするような直線（または曲線）を見つける方法です。

ビジネスの応用例

最小二乗法は、ビジネス分野でも多くの応用があります。たとえば、広告支出と売上の関係をモデル化する際に使用されます。広告支出を調整可能なパラメータとし、実際の売上とモデルの予測との差（残差）を最小化するような広告支出のモデルを作成します。このモデルを使用して、広告支出と売上の最適な関係を特定し、広告予算の最適化や収益の最大化に寄与します。

最小二乗法は、データに基づいてモデルのパラメータを調整し、観測データとモデルの適合度を向上させるための強力なツールです。ビジネス上の問題を数学的にモデル化し、最適な戦略や意思決定を導く際に役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# サンプルデータ
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2.1, 3.9, 5.5, 4.2, 5.1])

# 線形回帰モデルを作成し、学習
model = LinearRegression().fit(X, y)
predicted_y = model.predict(X)

# グラフ描画
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Actual Data')
plt.plot(X, predicted_y, color='red', label='Regression Line')

# 各データ点から回帰直線までの誤差を表示
for x_i, y_i, pred_y_i in zip(X, y, predicted_y):
    plt.plot([x_i, x_i], [y_i, pred_y_i], color='green', linestyle='--')

plt.title('Least Squares Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

上記のコードを実行すると、青い点で実際のデータ、赤い線で回帰直線、そして緑の破線で各データ点と回帰直線との誤差が表示されます。これにより、最小二乗法の考え方が視覚的に理解しやすくなります。

回帰直線

回帰直線は、2つの変数間の関係を表す直線です。1つの変数（独立変数または説明変数）がもう1つの変数（従属変数または目的変数）にどのように影響するかを示します。回帰直線は、回帰分析を使用してデータから導出され、変数間の関係を数学的にモデル化するのに役立ちます。

ビジネスの応用例

ビジネス分野では、回帰直線を使用してさまざまな問題を解決します。例えば、広告支出と売上の関係を分析する際、過去のデータから広告支出と売上の回帰直線を求めることがあります。この回帰直線を使用して、将来の広告支出に対する売上の予測を行います。また、製品の価格と売上、生産量とコスト、在庫レベルと需要など、さまざまなビジネス課題に回帰直線を適用することがあります。これにより、データに基づいた意思決定や戦略立案が可能になります。

回帰直線は、ビジネスにおいてデータ駆動型のアプローチをサポートし、将来の予測や最適化に向けた基盤を提供します。

Pythonコード

# 必要なライブラリのインポート
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# サンプルデータの作成
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 4, 5, 4, 5])

# 線形回帰モデルの作成と学習
model = LinearRegression().fit(X, y)

# 予測値の計算
predicted_y = model.predict(X)

# グラフの描画
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Actual Data')  # 実際のデータ点
plt.plot(X, predicted_y, color='red', label='Regression Line')  # 回帰直線
plt.title('Linear Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

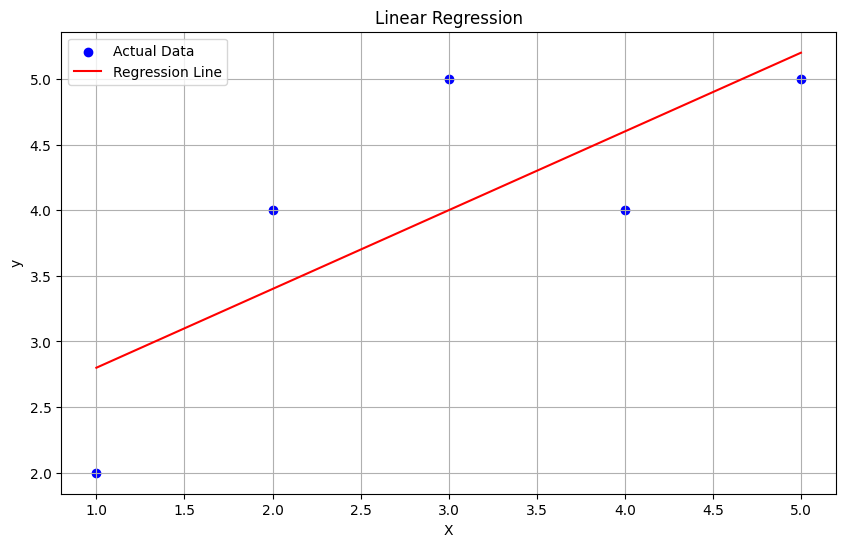
上記のコードは、サンプルデータに基づいて線形回帰を行い、その結果をグラフで表示するものです。このコードを実行すると、青い点で実際のデータ、赤い線で回帰直線が表示されるグラフが得られます。

正規分布

正規分布（またはガウス分布とも呼ばれます）は、統計学で最も一般的に使用される確率分布の一つです。その特徴は、ベル型のカーブを持つことであり、このカーブは左右対称で、平均値（μ）を中心にして広がります。また、分散（σ^2）が分布の広がり具合を制御します。正規分布は、多くの自然現象やデータセットに適用される統計的モデルです。

ビジネスの応用例

ビジネス分野では、正規分布がさまざまな応用を持ちます。たとえば、製造業で製品の寸法の分布が正規分布に従っているかを確認することがあります。正規分布に従う場合、製品の寸法のばらつきが予測可能で、品質管理において製品の仕様を設定するのに役立ちます。また、市場調査や消費者行動の分析においても、データが正規分布に従うことが前提とされることがあります。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 0, 0.1
s = np.random.normal(mu, sigma, 1000)
plt.hist(s, bins=30, density=True)
plt.title("Normal Distribution")
plt.show()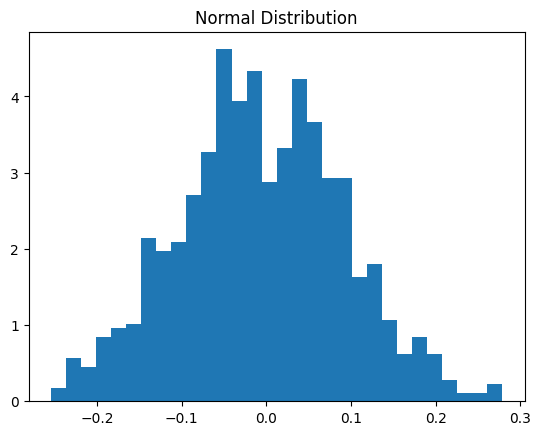

上記のPythonコードは、平均（mu）が0、標準偏差（sigma）が0.1の正規分布に従う乱数を生成し、その分布をヒストグラムとして可視化しています。この例では、データが正規分布に従う傾向を視覚的に示しています。

正規分布は、統計的な解析やモデリングにおいて基本的で、データの性質を理解し、予測を行う際に有用なツールです。データが正規分布に従う場合、統計的手法や仮定の適用が容易になり、意思決定に信頼性を持たせることができます。

連続的な確率変数

連続的な確率変数は、無限の可能性を持つ変数で、連続的な値を取ることができます。具体的な例として、身長、体重、時間、温度などが挙げられます。これらの変数は、どんな2つの値の間にも無数の他の値が存在し、離散的な値では表現しきれない幅広い範囲の値を取り得ます。連続的な確率変数は、実際に多くの現象やデータを表現するために使用されます。

ビジネスの応用例

ビジネス分野では、顧客データや市場データなど、連続的なデータを持つ変数を分析することが一般的です。例えば、顧客の年齢や購買額は連続的な変数です。これらのデータを分析することで、顧客セグメンテーション、ターゲット市場の特定、価格戦略の最適化など、さまざまなビジネス上の戦略や意思決定を行います。連続的なデータの分析は、ビジネスの洞察を得るために不可欠です。

連続的な確率変数は、実世界のデータや問題をモデル化し、数学的に扱うための重要な概念です。ビジネス分野では、このような変数を分析して戦略立案や意思決定を行い、競争力を向上させるために活用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# データ生成
x = np.linspace(-5, 5, 1000)
y = norm.pdf(x, 0, 1)  # 平均0、標準偏差1の正規分布

# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='Probability Density Function (PDF)')
plt.title('Continuous Random Variable - Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

連続的な確率変数をグラフに表現するためには、確率密度関数（Probability Density Function: PDF）を使用します。例として、正規分布（ガウス分布）を考えると、これは連続的な確率変数を表現するための最も一般的な分布の一つです。

上記のPythonコードは、正規分布の確率密度関数をグラフで表現するものです。これを通じて、連続的な確率変数の概念を視覚的に理解できます。

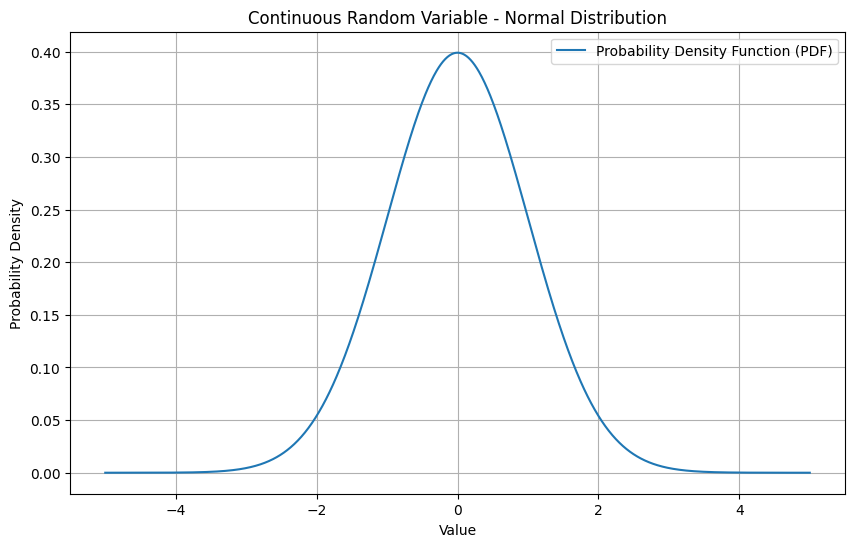
このグラフは、正規分布の確率密度関数を示しています。正規分布は、ビジネス、自然現象、社会科学など、多くの分野で見られるデータの分布をよく表しています。正規分布の形状は、平均値を中心にして左右対称で、平均値の周りにデータが集中していることを示しています。

正規分布の規格化

正規分布の規格化は、正規分布の性質を変えずに平均を0、分散を1に変換するプロセスを指します。この変換を行うことで、正規分布は「標準正規分布」と呼ばれる特別な正規分布になります。標準正規分布は、平均が0、分散が1であるため、統計的な比較や解析が容易になります。規格化は、データの尺度や範囲が異なる場合に、それらを共通の基準にするために使用されます。

ビジネスの応用例

ビジネス分野では、製品の品質データや顧客の購買データなど、さまざまなデータを規格化することがあります。例えば、異なる製品や市場でのデータを比較する場合、それらのデータを規格化して同じ尺度で評価することが有用です。品質管理においても、製品の異なる特性を比較する際に規格化が行われ、異なる指標を同じ基準で評価します。

Pythonコード

import numpy as np
data = np.array([50, 55, 53, 56, 54])
normalized_data = (data - np.mean(data)) / np.std(data)
print(normalized_data)

[-1.74831455  0.6799001  -0.29138576  1.16554303  0.19425717]

上記のPythonコードは、データを規格化する例です。与えられたデータを平均値で中心化し（各データから平均を引き算）、標準偏差でスケーリングする（各データを標準偏差で割る）ことによって、データを標準正規分布に規格化しています。規格化されたデータは平均が0で、分散が1の標準正規分布になります。

# Given data and normalization
data = np.array([50, 55, 53, 56, 54])
normalized_data = (data - np.mean(data)) / np.std(data)

# Plotting
plt.figure(figsize=(10, 6))
plt.bar(range(len(data)), data, label='Original Data', alpha=0.6)
plt.bar(range(len(normalized_data)), normalized_data, label='Normalized Data', alpha=0.6, color='red')
plt.axhline(0, color='black', linestyle='--', linewidth=0.7)  # zero line for reference
plt.title('Data Normalization')
plt.xlabel('Data Index')
plt.ylabel('Value')
plt.legend()
plt.grid(True, axis='y')
plt.xticks(range(len(data)))
plt.tight_layout()
plt.show()

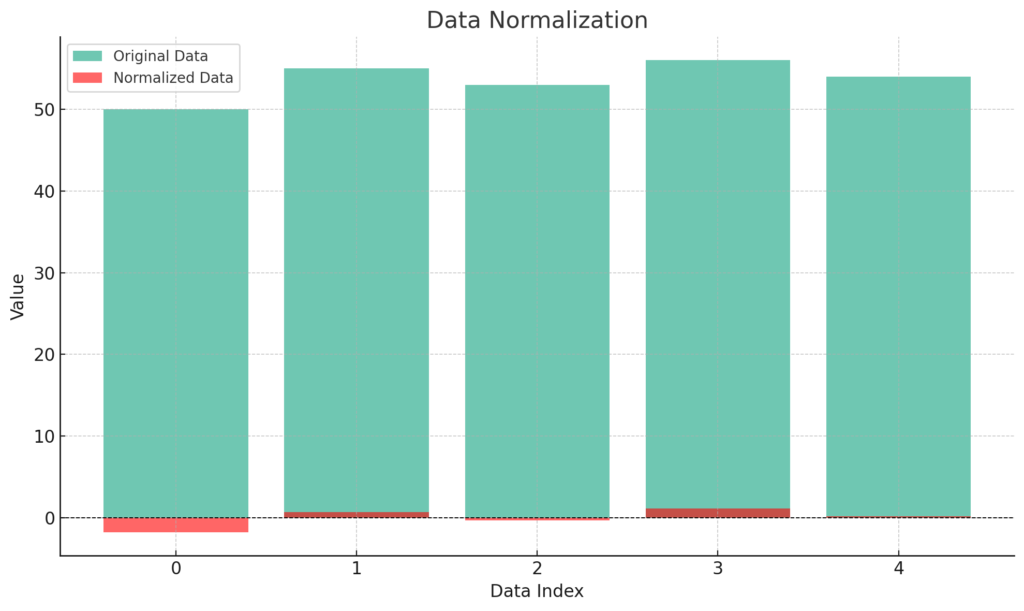
このグラフは、元のデータと正規化されたデータを並べて表示しています。青色の棒は元のデータを、赤色の棒は正規化されたデータを示しています。

正規化は、データを平均0、標準偏差1に変換するプロセスです。このプロセスにより、異なる尺度や単位のデータを比較しやすくできます。正規化されたデータは、データの形状やパターンを保持しながら、平均が0になるように中央にシフトします。​

正規分布の規格化は、統計解析や機械学習においてデータの前処理ステップとして重要であり、異なるデータセットを比較しやすくし、モデルの性能を向上させるのに役立ちます。

正規分布の分散

正規分布の分散は、データセット内の各データ点が平均からどれだけ離れているかを数値化した尺度です。分散はデータの散らばり具合を表し、値が大きいほどデータが平均から離れて散らばっていることを示します。正規分布の分散は、データのばらつきを数学的に捉えるために使用されます。

ビジネスの応用例

ビジネス分野では、正規分布の分散を使用してさまざまな問題に対処します。例えば、製品の品質管理において、品質データの分散を評価し、品質の一貫性を確認します。また、売上データの分析において、売上の変動の大きさを示すために分散を使用します。分散が大きい場合、売上に大きな変動があることを示し、需要予測や在庫管理の改善策を検討する方向性を提供します。

Pythonコード

variance = np.var(data)
print(variance)

4.24

上記のPythonコードは、与えられたデータセットの分散を計算する例です。np.var()関数を使用してデータの分散を計算し、その結果を出力します。

以下のコードは、正規分布の確率密度関数を表示し、その分散を強調表示するものです。

from scipy.stats import norm

# データ生成
x = np.linspace(-5, 5, 1000)
y = norm.pdf(x, 0, np.sqrt(4.24))  # 平均0、標準偏差sqrt(4.24)の正規分布

# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='Probability Density Function (PDF)')
plt.fill_between(x, y, where=(x > -2*np.sqrt(4.24)) & (x < 2*np.sqrt(4.24)), color='yellow', alpha=0.5, label='Variance (68.3%)')
plt.title('Normal Distribution with Variance')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

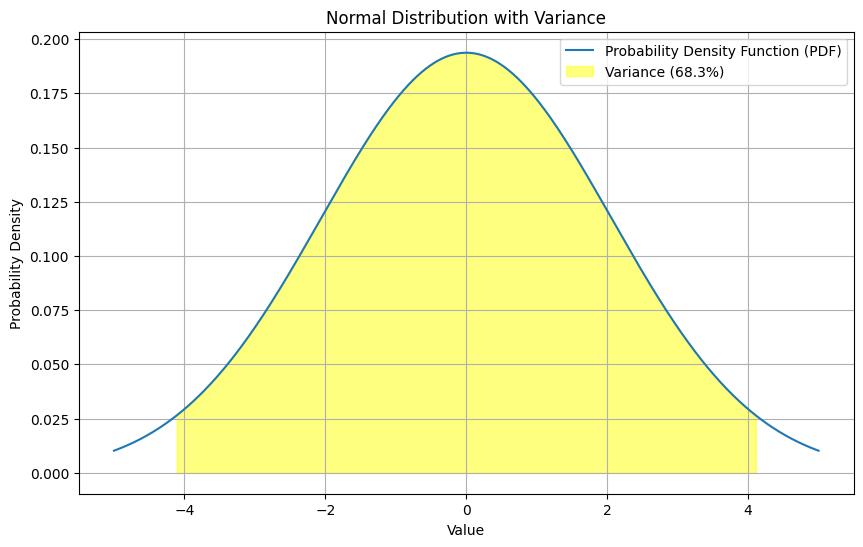
このグラフは、正規分布の確率密度関数を示し、約68.3%のデータが平均±1標準偏差の間に存在することを強調表示しています。

正規分布の分散は、データの特性を理解し、品質管理、リスク評価、意思決定に役立ちます。データの分散を評価することで、データセットの安定性や予測の信頼性を向上させるのに寄与します。

正規分布と標準正規分布

正規分布は任意の平均と分散を持つ確率分布です。標準正規分布は、正規分布の平均が0、分散が1の特殊なケースを指します。

1. 正規分布: 正規分布（またはガウス分布）は、統計学でよく使われる確率分布です。正規分布は、ベル型のカーブを持ち、左右対称で、特徴的な山型の形状をしています。正規分布は、実際に多くの現象やデータに適用され、データの分布を記述するのに役立ちます。正規分布は、平均（μ）と分散（σ^2）という2つのパラメータによって特徴づけられ、平均値を中心にデータが散らばっています。
2. 標準正規分布: 標準正規分布は、正規分布の一特殊なケースで、平均（μ）が0で、分散（σ^2）が1の正規分布です。つまり、標準正規分布は、平均がゼロで、データが平均からどれだけ離れているかを「標準偏差」の単位で表現した分布です。標準正規分布は、通常、Z分布とも呼ばれます。

ビジネスの応用例

ビジネス分野では、標準正規分布を使用して品質管理やデータの評価を行うことがあります。特定の製品の品質データを標準正規分布に基づいて評価することで、その品質が平均からどの程度離れているかを「Zスコア」として計算できます。このZスコアは、品質改善策を決定する際に役立ちます。また、標準正規分布を使用して、データの正規化や比較を行うことがあります。

Pythonコード

standardized_data = (data - np.mean(data)) / np.std(data)

上記のPythonコードは、データを標準正規分布に変換（規格化）する例です。データを平均値で中心化し（各データから平均を引く）、標準偏差でスケーリングする（各データを標準偏差で割る）ことによって、データを標準正規分布に変換しています。

from scipy.stats import norm

# Generating data for normal distribution and standard normal distribution
x = np.linspace(-5, 5, 1000)
y_normal = norm.pdf(x, np.mean(data), np.std(data))  # normal distribution with sample mean and std deviation
y_standard = norm.pdf(x, 0, 1)  # standard normal distribution

# Plotting
plt.figure(figsize=(12, 7))
plt.plot(x, y_normal, label='Normal Distribution (μ={}, σ^2={:.2f})'.format(np.mean(data), np.var(data)))
plt.plot(x, y_standard, label='Standard Normal Distribution (μ=0, σ^2=1)', linestyle='--')
plt.title('Normal Distribution vs. Standard Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

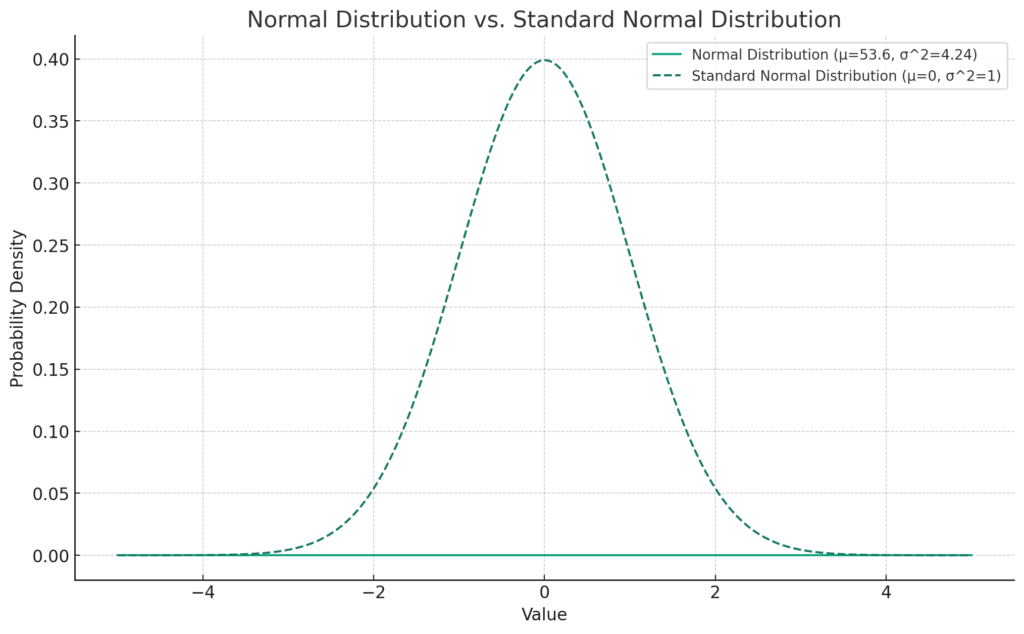
上記のグラフは、正規分布と標準正規分布を比較するものです。

• 青い線: サンプルデータの平均と標準偏差を持つ正規分布を示しています。
• オレンジの破線: 平均0、分散1の標準正規分布を示しています。

このグラフを通じて、標準正規分布がどのように通常の正規分布と異なるのか、またどのようにそれを特徴づけるのかを視覚的に理解できます。​​

正規分布と標準正規分布は、データの分析や統計的な処理において基本的な概念であり、データの性質を理解し、統計的な推論を行うための重要なツールです。標準正規分布は、異なるデータセットを比較しやすくし、統計的な計算を簡略化するために利用されます。

正規分布等分散の関係

等分散とは、2つ以上のグループのデータの分散が等しいことを指します。正規分布のデータが等分散である場合、多くの統計的手法が適切に使用できます。

1. 等分散: 等分散は、統計学やデータ分析の文脈で使用される用語で、複数のデータグループまたはサンプル間で分散が等しいことを指します。つまり、異なるグループやサンプルのデータのばらつきが同じであるという性質を示します。等分散は、統計的な推論や比較を行う際に重要な前提条件の一つです。
2. 正規分布と等分散: 正規分布のデータが等分散である場合、異なるグループやサンプル間でのデータのばらつきが均等であることを示します。この性質は、統計的な仮説検定や分散分析などの統計手法において重要です。等分散の前提が満たされている場合、統計的な結果が信頼性が高く、適切に解釈できることが多いです。

ビジネスの応用例

ビジネス分野では、異なる製品ライン、店舗、地域などのデータを比較する際に等分散の考慮が重要です。例えば、複数の店舗の売上データを比較し、どの店舗が他の店舗と比べて売上が均等にばらついているかを評価します。等分散が満たされている場合、適切な戦略を立案し、経営資源を最適に配置するのに役立ちます。

Pythonコード

# Generating data for demonstrating homoscedasticity (等分散)
np.random.seed(0)
group1 = np.random.normal(50, 10, 100)  # mean 50, std 10
group2 = np.random.normal(60, 10, 100)  # mean 60, std 10

# Plotting
plt.figure(figsize=(12, 7))
plt.scatter(np.ones_like(group1) * 1, group1, alpha=0.6, label='Group 1', s=50)
plt.scatter(np.ones_like(group2) * 2, group2, alpha=0.6, label='Group 2', s=50)
plt.axhline(np.mean(group1), color='blue', linestyle='--')
plt.axhline(np.mean(group2), color='orange', linestyle='--')
plt.title('Demonstration of Homoscedasticity (Equal Variance)')
plt.xlabel('Group')
plt.ylabel('Value')
plt.xticks([1, 2], ['Group 1', 'Group 2'])
plt.legend()
plt.grid(True, axis='y')
plt.tight_layout()
plt.show()

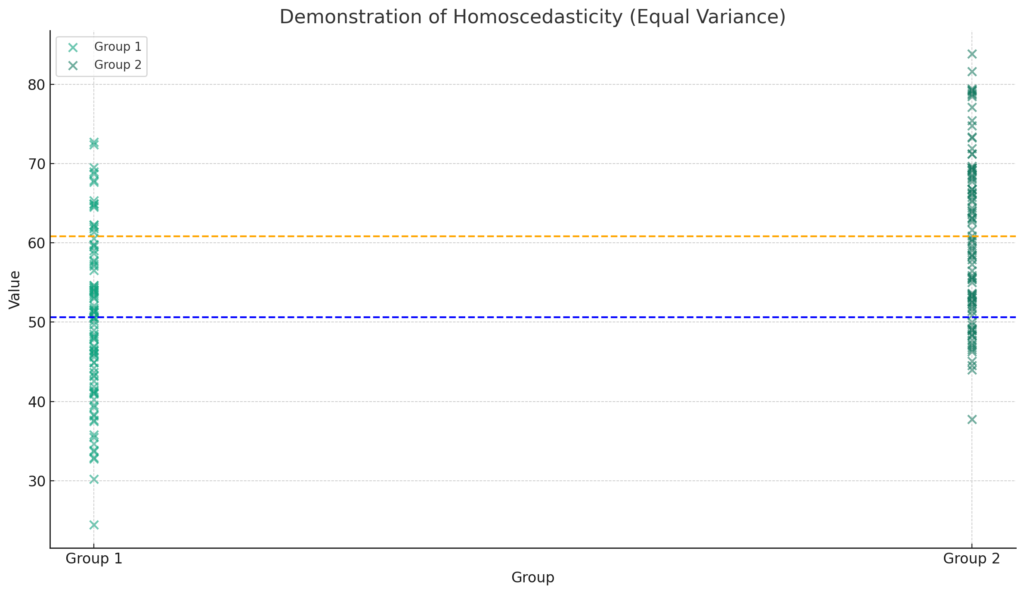
このグラフは、2つのグループ（Group 1とGroup 2）のデータを示しており、両方のグループが等分散（同じ分散）を持つことを視覚的に示しています。

• 青の点: Group 1のデータ
• オレンジの点: Group 2のデータ
• 青の破線: Group 1の平均
• オレンジの破線: Group 2の平均

このグラフを見ることで、2つのグループが異なる平均を持っている一方で、データの散らばり具合（分散）は似ていることがわかります。このような等分散の性質は、統計的な分析や比較を行う際の重要な前提条件となります。​

正規分布等分散の条件が満たされると、統計的な解析が信頼性が高く、適切に行えるため、データの比較や意思決定において重要な要素となります。データの等分散性を確認するためには、適切な統計的テストを使用することが一般的です。

正規分布をグラフ化する

正規分布をグラフに描くことは、データの分布や特性を視覚的に理解する手法の一つです。正規分布は、ベル型のカーブを持つため、その形状や中心傾向がグラフから読み取りやすく、データセットの特性を把握するのに役立ちます。

ビジネスの応用例

ビジネス分野では、さまざまなデータを正規分布としてグラフ化することがあります。例えば、製品の品質データ、顧客の購買データ、市場の需要データなど、異なるビジネス領域でデータの分布を視覚化します。これにより、以下の点が達成されます。

• 異常値の発見: グラフを通じて、異常なデータポイントが他と比べてどのように異なるかを確認できます。
• 傾向の可視化: データの中心傾向やばらつきをグラフから理解し、ビジネス戦略に役立てることができます。

Pythonコード

import matplotlib.pyplot as plt
plt.hist(data, bins=30, density=True)
plt.title("Normal Distribution of Data")
plt.show()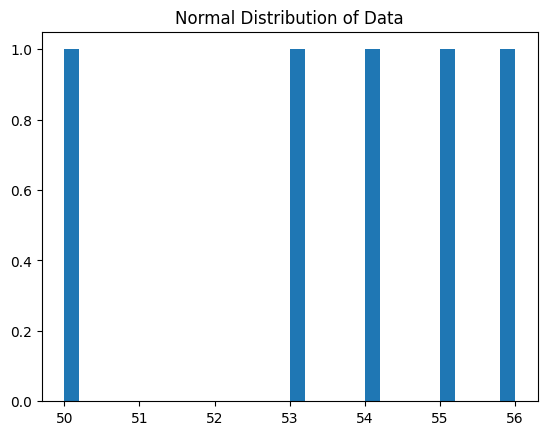

上記のPythonコードは、データを正規分布としてヒストグラムで表示する例です。plt.hist()関数を使用してデータを30のビンに分割し、分布をグラフ化します。グラフのタイトルを設定して、データの分布が正規分布にどの程度近いかを視覚的に確認できます。

正規分布のグラフ化は、データの特性を素早く理解する手法であり、データ駆動型の意思決定や品質管理において有用です。グラフを通じて、データの特徴を視覚的に把握できます。

標準偏差の範囲を決める不等式

標準偏差の範囲を決める不等式は、データの分布が正規分布に従っている場合、データポイントが平均からどの程度ばらついているかを示します。一般的に、以下のような範囲が考えられます。

• 約68%のデータポイントは、平均±1標準偏差の範囲内に存在します。
• 約95%のデータポイントは、平均±2標準偏差の範囲内に存在します。
• 約99.7%のデータポイントは、平均±3標準偏差の範囲内に存在します。

ビジネスの応用例

ビジネス分野では、品質管理やプロセス改善などの多くの領域でこの原則を活用します。例えば、製品の寸法や重量のデータが正規分布に従っている場合、標準偏差を使用して製品の品質を評価できます。製品の寸法が平均±2標準偏差の範囲内にある場合、製品はほぼすべての要件を満たしており、品質が高いと判断できます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
data = np.random.randn(1000)
mean = np.mean(data)
std_dev = np.std(data)
plt.hist(data, bins=30, density=True)
plt.axvline(mean, color='red', label='Mean')
plt.axvline(mean + std_dev, color='green', linestyle='--', label='Mean + 1 SD')
plt.axvline(mean - std_dev, color='green', linestyle='--', label='Mean - 1 SD')
plt.legend()
plt.show()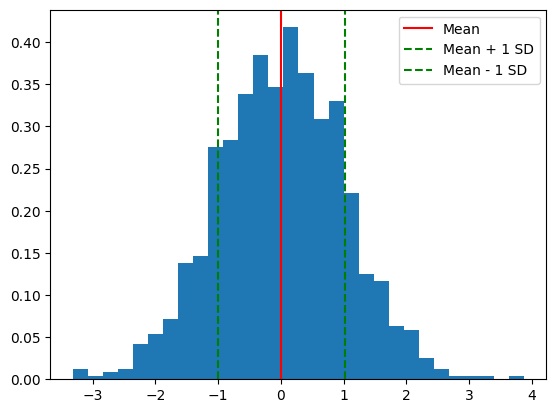

上記のPythonコードは、正規分布に従うデータをヒストグラムで表示し、標準偏差の範囲を示すための直線を追加しています。赤線は平均を示し、緑の破線は平均±1標準偏差の範囲を示しています。このグラフを通じて、データの分布がどの程度ばらついているかが視覚的に確認できます。

標準偏差の範囲を考慮することは、品質管理やリスク評価などのビジネス上の重要な決定において、データの信頼性を評価するのに役立ちます。

チェビシェフの不等式の証明

チェビシェフの不等式の要点: チェビシェフの不等式は、任意の確率分布に対して、平均からk標準偏差以上離れたデータの割合が\( \frac{1}{k^2} \)以下であることを示す不等式です。具体的には、以下のように表されます。

\[P(\left| X – \mu \right| \geq k\sigma) \leq \frac{1}{k^2}\]

ここで、\(X\)は確率変数、\(\mu\)は平均、\(\sigma\)は標準偏差、\(k\)は任意の正の整数です。

ビジネスの応用例

チェビシェフの不等式は、正規分布でないデータや、データの分布について詳細な情報が得られない場合に役立ちます。具体的なビジネス応用例としては、以下のようなものが考えられます。

• 株価データ: 株価は正規分布に従わないことがよくあります。チェビシェフの不等式を用いて、ある日の株価の変動が平均からどれだけ外れたものであるかを評価し、リスク管理に活用できます。
• 販売データ: 製品の販売データにおいて、異常な販売数や売上額を検出するためにチェビシェフの不等式を利用できます。たとえば、特定の製品の売上が平均から2標準偏差以上外れた場合、これを異常な売上として監視できます。

チェビシェフの不等式の証明: チェビシェフの不等式は、確率論と統計学の理論に基づいて証明されます。証明は複雑であり、数式的に詳細になりますが、基本的なアイデアは次のとおりです。

• 平均からk標準偏差以上離れたデータの確率を最大化するために、データの分布について何も知らないと仮定します。
• 標準化した変数（平均を0、標準偏差を1にする変数）を導入します。これにより、データを単位標準偏差で測定できます。
• 標準化された変数の確率密度関数を用いて、k標準偏差以上離れた領域の面積を計算します。
• マークオフの不等式などの数学的テクニックを使用して、面積を制約します。

Pythonコード

# Generating Chebyshev's inequality plot

# Sample data from a normal distribution (for demonstration purposes)
mu = 0
sigma = 1
X = np.linspace(-5, 5, 1000)
pdf = norm.pdf(X, mu, sigma)

# For Chebyshev's inequality
k_values = [1, 2, 3]
areas = []

plt.figure(figsize=(12, 7))
plt.plot(X, pdf, label='Probability Density Function', color='blue')

# Highlight the areas corresponding to Chebyshev's inequality for various k values
for k in k_values:
    mask = (X < mu - k*sigma) | (X > mu + k*sigma)
    area = np.sum(pdf[mask]) * (X[1] - X[0])  # Approximate integral
    areas.append(area)
    plt.fill_between(X, pdf, where=mask, alpha=0.4, label=f'k={k}, Area ≤ {1/k**2:.2f}', interpolate=True)

plt.title("Demonstration of Chebyshev's Inequality")
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend(loc='upper left')
plt.grid(True)
plt.tight_layout()
plt.show()

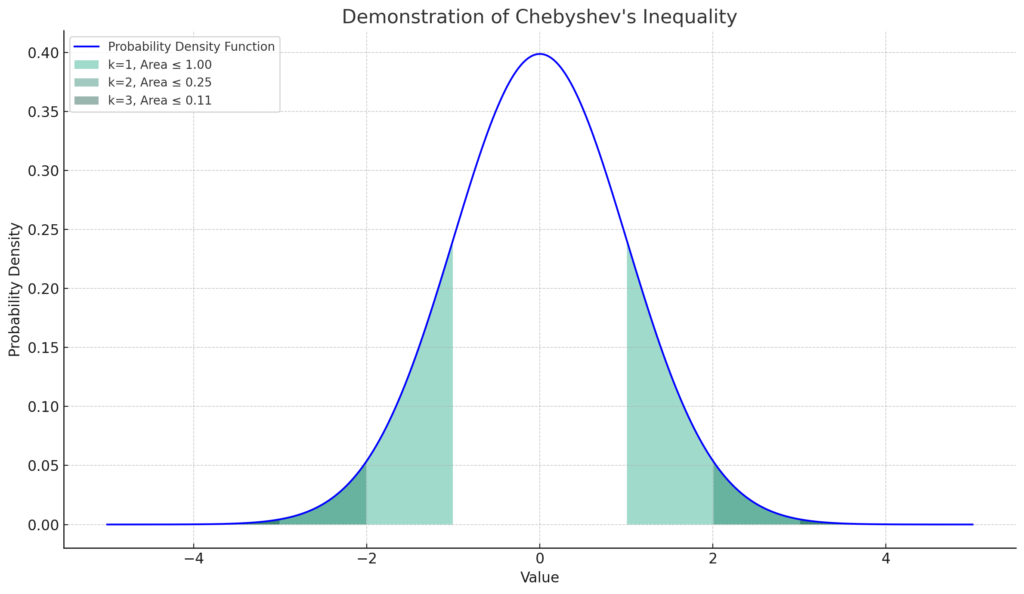
このグラフは、チェビシェフの不等式を視覚的に示すものです。

• 青い線: 確率密度関数 (PDF) を示しています。
• シェーディングされた領域: 平均から \( k \) 標準偏差以上離れた部分を示しています。

チェビシェフの不等式によれば、これらのシェーディングされた領域の面積（確率）は \( \frac{1}{k^2} \) 以下であるとされます。このグラフでは、\( k \) の値が 1, 2, 3 の場合のシェーディング領域を表示しています。それぞれの \( k \) の値に対して、実際の面積が \( \frac{1}{k^2} \) よりも小さいことが視覚的にわかります。

このグラフは、任意の確率分布に対して、チェビシェフの不等式がどのように適用されるかを示しています。

分散の形を表す指標

分散と標準偏差は、データのばらつきや散らばり具合を数値化するための指標です。

• 分散 (Variance): データポイントが平均からどれだけ離れているかの平均値です。分散が大きいほど、データは平均から散らばっています。
• 標準偏差 (Standard Deviation): 分散の平方根で、データポイントが平均からどれだけ離れているかの平均的な距離を示します。標準偏差は分散の正の平方根です。

ビジネスの応用例

これらの指標は、ビジネスや経済分野でさまざまな用途に活用されます。

• 売上データの管理: 月次の売上データの分散や標準偏差を計算し、売上のばらつきを確認します。これにより、需要予測の精度を向上させ、在庫管理や生産計画を最適化できます。分散や標準偏差が大きい場合、需要の不安定性が高いことを示唆し、リスク管理の必要性が高まります。

Pythonコード

variance = np.var(data)
std_deviation = np.std(data)

0.9795236351945662

Pythonを使用して分散と標準偏差を計算できます。上記のコード例では、データから分散と標準偏差を計算しています。分散は variance で、標準偏差は std_deviation で示されています。

# Generating a histogram to visually demonstrate variance and standard deviation

# Generating data
data_points = np.random.normal(0, 1, 1000)

# Plotting
plt.figure(figsize=(12, 7))
plt.hist(data_points, bins=30, density=True, alpha=0.7, color='lightblue', edgecolor="k", label="Data Distribution")

# Mean, Variance, and Standard Deviation
mean = np.mean(data_points)
variance = np.var(data_points)
std_deviation = np.std(data_points)

# Highlighting mean, +/- 1 std deviation
plt.axvline(mean, color='red', linestyle='dashed', linewidth=1, label=f"Mean: {mean:.2f}")
plt.axvline(mean + std_deviation, color='green', linestyle='dashed', linewidth=1, label=f"+1 Std Deviation: {std_deviation:.2f}")
plt.axvline(mean - std_deviation, color='green', linestyle='dashed', linewidth=1)

plt.title('Demonstration of Variance and Standard Deviation')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()
plt.grid(True, axis='y')
plt.tight_layout()
plt.show()

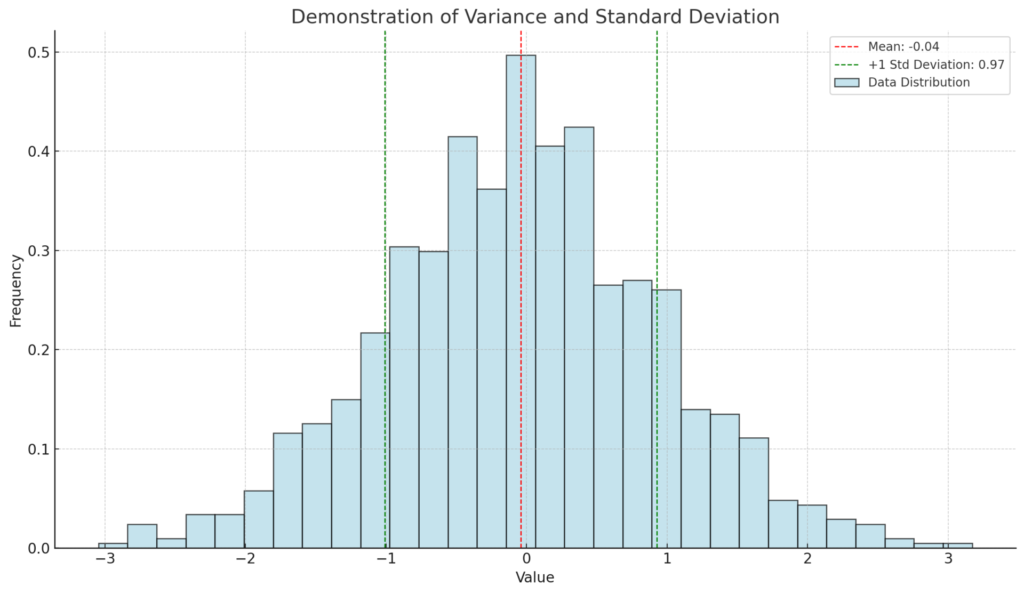
このヒストグラムは、分散と標準偏差を視覚的に示しています。

• 薄い青色の棒: データの分布を示しています。
• 赤い破線: データの平均値を示しています。
• 緑の破線: 平均値の±1標準偏差を示しています。

このヒストグラムを通じて、データの中心（平均）と、データがその中心からどれだけ散らばっているか（標準偏差）を視覚的に理解できます。​

分散と標準偏差は、データのばらつきを理解し、意思決定プロセスに情報を提供するために広く使用される統計的指標です。

ド・モアブル – ラプラスの定理

ド・モアブル – ラプラスの定理は、連続的な確率変数の関数の期待値を求めるための重要な確率論の公式です。

1. ド・モアブル – ラプラスの定理: ド・モアブル – ラプラスの定理は、確率分布を持つ連続的な確率変数Xに対して、関数g(X)の期待値を求める方法を提供します。定理の数学的な表現は次のようになります。 \[E[g(X)] = \int_{-\infty}^{\infty} g(x) \cdot f(x) \, dx\] ここで、Eは期待値を表し、g(X)はXの関数、f(x)はXの確率密度関数です。

ビジネスの応用例

ド・モアブル – ラプラスの定理は、保険業界などで活用されます。保険料の算定において、異なるリスク要因が組み合わさる場合、それぞれのリスク要因の確率分布と関数を考慮して、保険料を計算するのに役立ちます。たとえば、車の保険料を算定する際、運転履歴、車の種類、地域などのリスク要因を組み合わせて、ド・モアブル – ラプラスの定理を使用して保険料を決定できます。

この定理は、確率論と統計学の分野でとても重要であり、確率分布と関数の期待値を計算する際に広く活用されています。保険、ファイナンス、科学、エンジニアリングなど多くの分野でリスク評価と意思決定に役立ちます。

Pythonコード

# Demonstrating the concept using a simple function and a normal distribution

# Consider a simple function g(x) = x^2
def g(x):
    return x**2

# Sample data from a normal distribution (for demonstration purposes)
X = np.linspace(-5, 5, 1000)
pdf = norm.pdf(X, 0, 1)
g_values = g(X)

# Plotting
plt.figure(figsize=(12, 7))

# Plotting the probability density function
plt.plot(X, pdf, label='Probability Density Function (f(x))', color='blue')

# Plotting g(X)
plt.plot(X, g_values, label='Function g(X) = X^2', color='green', linestyle='--')

plt.fill_between(X, pdf, alpha=0.1, color='blue')
plt.fill_between(X, g_values, alpha=0.1, color='green')

plt.title("Demonstration of de Moivre–Laplace Theorem")
plt.xlabel('Value of X')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

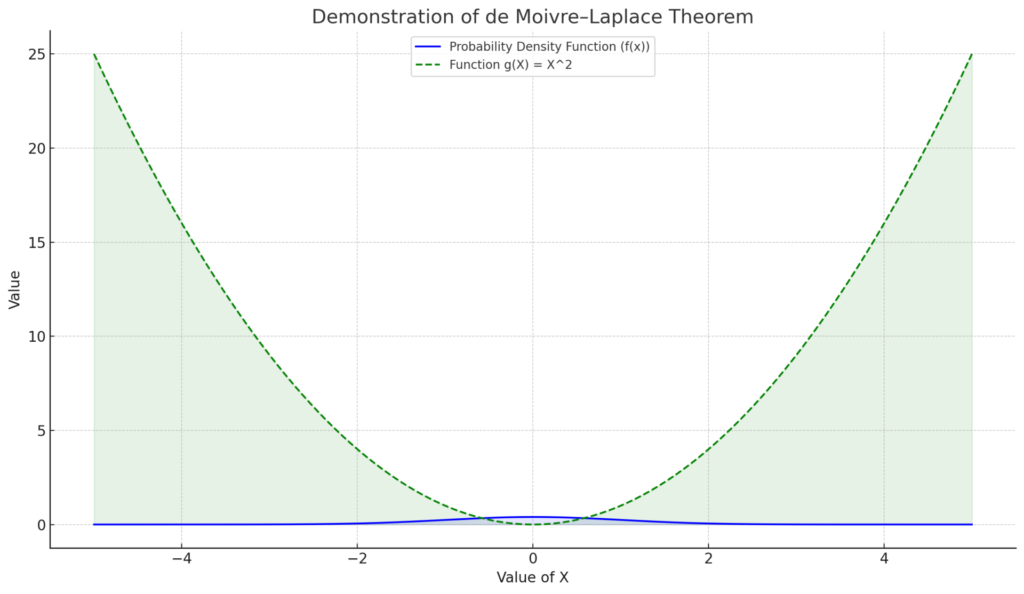
このグラフは、ド・モアブル – ラプラスの定理の概念を視覚的に示すものです。

• 青い線: 確率密度関数 \( f(x) \) を示しています。この例では、正規分布を示しています。
• 緑の破線: 関数 \( g(X) = X^2 \) の値を示しています。

このグラフを通じて、確率変数 \( X \) の関数 \( g(X) \) の期待値を求めるために、確率密度関数と関数の積の積分を取るという概念を理解できます。具体的には、青と緑の領域がそれぞれの関数の積分（面積）を示しており、ド・モアブル – ラプラスの定理に従って、これらの積分を取ることで期待値を求めることができます。

ポアソン分布

ポアソン分布は、事象が一定の期間や範囲内でランダムに発生する場合、その事象の回数が従う確率分布です。

ポアソン分布の特徴:
ポアソン分布は、次のような特徴を持っています。

1. 事象が連続的に発生するのではなく、離散的に発生する場合に適しています。例えば、電話の着信、交通事故の発生、誤字の数などが該当します。
2. 事象の発生率が一定であると仮定されます。つまり、ある期間内での平均的な発生回数が分布のパラメータ λ (ラムダ) で表され、それは一定です。
3. 各事象の発生が独立であると仮定されます。つまり、1つの事象の発生が他の事象に影響を与えないと仮定されます。

ビジネスの応用例

ポアソン分布はビジネスや実務において幅広く利用されます。

1. コールセンターの電話対応時間の予測: コールセンターでは、1時間あたりの電話の着信数をポアソン分布としてモデル化し、スタッフの配置や対応時間の最適化を計画します。
2. 交通事故の発生予測: あるエリアでの1日あたりの交通事故の発生数をポアソン分布としてモデル化し、交通安全対策や保険料の設定に活用します。
3. ウェブサイトへのアクセス数の予測: ウェブサイトへのアクセス数は一定期間内にランダムに発生するため、ポアソン分布を使用して将来のアクセス数を予測し、サーバーのリソースを最適化します。

Pythonコード

import numpy as np
lambda_value = 5
poisson_sample = np.random.poisson(lambda_value, 1000)
plt.hist(poisson_sample, bins=30)
plt.title("Poisson Distribution")
plt.show()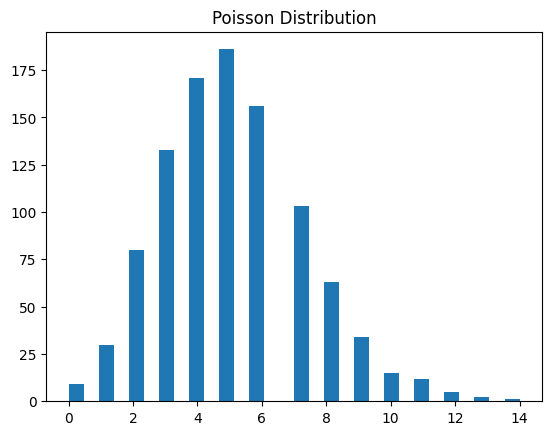

上記のPythonコードは、ポアソン分布をシミュレーションし、その分布をヒストグラムで可視化しています。λ (ラムダ) の値を変更することで、平均的な発生回数を調整できます。このコードはポアソン分布を理解し、データの生成と可視化に役立ちます。

二項分布をポアソン分布で近似する

1. 二項分布: 二項分布は、独立なベルヌーイ試行をn回行ったときの成功回数が従う確率分布です。つまり、成功（例: コインが表になる）と失敗（裏になる）の2つの結果しかない試行をn回繰り返す場合、成功回数が従う確率分布です。
2. ポアソン分布: ポアソン分布は、一定の期間や範囲内でランダムに発生する事象の回数が従う確率分布です。例えば、一定時間内の電話の着信数や事故の発生数がポアソン分布に従うことがあります。
3. 近似: 二項分布をポアソン分布で近似する場合、試行回数 \( n \) がとても大きく、成功確率 \( p \) がとても小さい場合に適用されます。つまり、大量の試行があり、成功が稀な状況です。この場合、二項分布のパラメータ \( np \) はポアソン分布のパラメータ \( \lambda \) に近似されます。

ビジネスの応用例

ビジネスにおいて、この近似を利用する具体的な例は、品質管理です。大量の商品を生産する際、欠陥品の発生確率がとても低い場合、その欠陥品の数は二項分布でモデル化されます。しかし、欠陥品の発生確率がとても低い場合、\( n \) が大きく \( p \) が小さいため、この二項分布をポアソン分布で近似できます。これにより、品質管理の基準を設定しやすくなります。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
n = 1000
p = 0.005
lambda_value = n * p
binomial_sample = np.random.binomial(n, p, 10000)
poisson_sample = np.random.poisson(lambda_value, 10000)
plt.hist(binomial_sample, bins=30, alpha=0.5, label='Binomial')
plt.hist(poisson_sample, bins=30, alpha=0.5, label='Poisson')
plt.legend()
plt.show()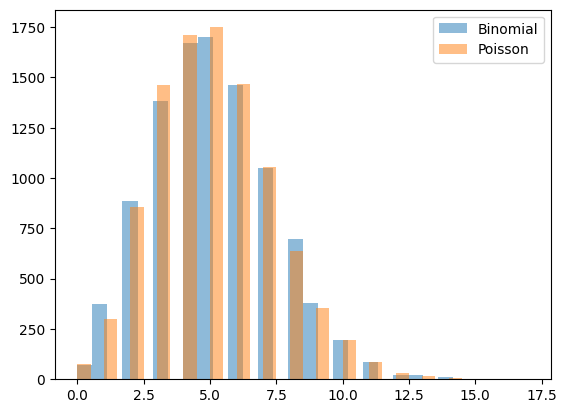

上記のPythonコードは、二項分布とポアソン分布をシミュレーションし、その結果をヒストグラムで可視化しています。このコードは、二項分布がポアソン分布に近似される様子を示しています。成功確率 \( p \) と試行回数 \( n \) の値を調整して、近似の挙動を観察できます。

ポアソン分布の導出

ポアソン分布の導出は、二項分布から始まります。二項分布は、独立なベルヌーイ試行をn回行ったときの成功回数が従う確率分布です。成功確率を\( p \)、試行回数を\( n \)とすると、二項分布の確率質量関数は以下のように表されます。

\[
P(X = k) = \binom{n}{k} p^k (1 – p)^{n – k}
\]

ここで、\( k \) は成功の回数です。次に、ポアソン分布について考えます。ポアソン分布は、一定の期間や範囲内でランダムに発生する事象の回数が従う確率分布で、パラメータ\( \lambda \)を持ちます。ポアソン分布の確率質量関数は以下のように表されます。

\[
P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}
\]

ここで、\( k \) は事象の発生回数です。

二項分布をポアソン分布に近似するためには、以下の条件を考えます:

1. 試行回数 \( n \) がとても多い（\( n \) が大きい）。
2. 成功確率 \( p \) がとても小さい（\( p \) が小さい）。

この場合、\( np = \lambda \) となるような\(\lambda\)を見つけます。そして、二項分布の確率質量関数をポアソン分布の確率質量関数で近似します。具体的には、\( n \) が大きいため二項分布の確率質量関数から\( n \) を無限大に近づけ、\( p \) が小さいため\( p \) を無限小に近づける操作を行います。このとき、\( np \) を一定の\(\lambda\)に保つように調整します。すると、二項分布がポアソン分布に収束することが示されます。

ビジネスの応用例

ビジネスにおいて、この導出の理解はコールセンターの例など、稀な事象の発生をモデル化する際に役立ちます。コールセンターでの1時間あたりの着信数をポアソン分布としてモデル化する場合、試行回数がとても多く（たくさんの電話がかかってくる）、成功確率がとても小さい（電話がかかってくる確率が低い）場合に、ポアソン分布が適切な近似となります。このような状況でポアソン分布を使用することで、着信数の予測やリソースの適切な配置が行いやすくなります。

ハインリッヒの法則

ハインリッヒの法則は、産業安全に関する法則の一つで、事故の発生とその重要度に関する理論です。この法則は、次のような考え方に基づいています。

1. ある組織や施設における事故は、重大事故、軽微事故、無傷事故の3つのカテゴリーに分類できます。重大事故は最も深刻で、死傷者や大規模な損害を伴います。軽微事故は比較的軽度で、怪我や損害はあるものの、重大ではありません。無傷事故は、怪我や損害が発生しない事故です。
2. ハインリッヒの法則は、これらの事故カテゴリーの間に一定の関係があると主張します。具体的には、無傷事故が多く発生する状況では、軽微事故も多く発生し、軽微事故が多い状況では重大事故も多く発生するとされます。言い換えれば、無傷事故の削減が軽微事故および重大事故の削減につながるとされています。
3. この法則は、組織や施設が無傷事故の削減に注力し、その結果軽微事故および重大事故も減少することを示唆しています。つまり、事故の発生率を下げるためには、軽微な事故や無傷事故にも積極的に取り組む必要があるという考え方です。

ビジネスの応用例

ハインリッヒの法則は、工場や施設の安全管理においてとても重要です。

• 安全文化の構築: 組織内で安全意識を高め、従業員に軽微な事故や無傷事故の報告を奨励することが、重大事故のリスクを低減するのに役立ちます。
• トレーニングと教育: 従業員に対する安全トレーニングと教育を行い、事故の予防と対応能力を向上させることが、ハインリッヒの法則に基づいたアプローチの一部です。
• データ収集と分析: 軽微な事故や無傷事故のデータを収集し、定期的に分析することで、組織がどの方向に向かって進化しているかを監視し、改善策を実施できます。

ハインリッヒの法則を適切に活用することで、組織や施設の安全性を向上させ、重大事故の発生を減少させます。

Pythonコード

ハインリッヒの法則の概念をグラフで視覚的に表現するために、異なる種類の事故（重大事故、軽微事故、無傷事故）の発生頻度を棒グラフで示します。このグラフは、無傷事故が最も頻繁に発生し、軽微事故と重大事故の発生頻度がそれぞれ減少することを示しています。これは、ハインリッヒの法則の核心的な主張を反映しています。

以下は、この概念をグラフで表現するPythonコードです。

import matplotlib.pyplot as plt

# データの設定
categories = ['Major Accidents', 'Minor Accidents', 'No-injury Accidents']
frequencies = [1, 10, 300]  # 仮の事故発生頻度

# グラフの描画
plt.figure(figsize=(10, 6))
plt.bar(categories, frequencies, color=['red', 'yellow', 'green'])
plt.xlabel('Type of Accident')
plt.ylabel('Frequency')
plt.title('Representation of Heinrich\'s Law')
plt.tight_layout()

plt.show()

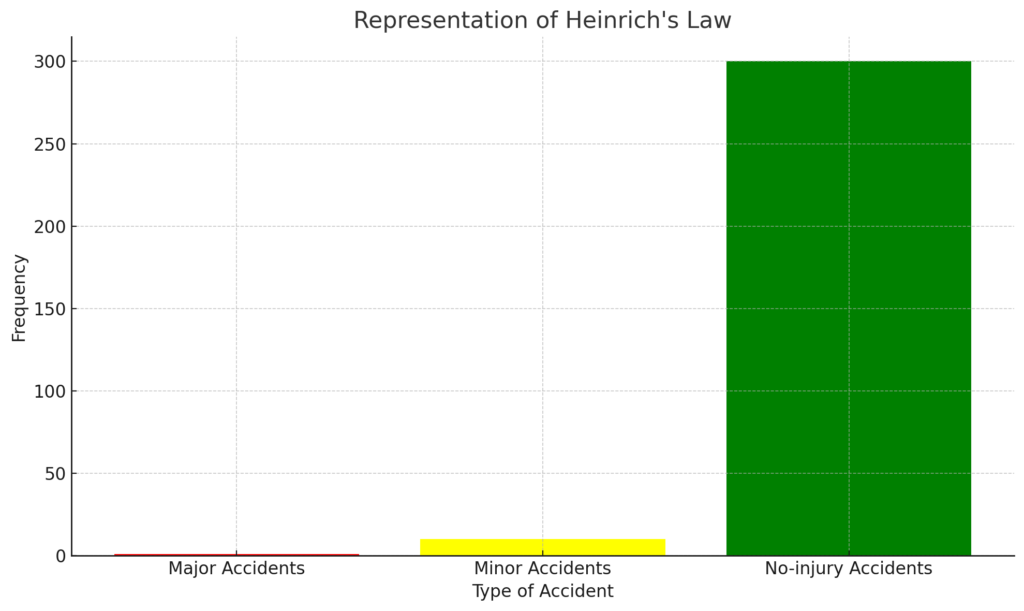
上記のグラフは、ハインリッヒの法則の主要な考え方を示しています。それによれば、重大な事故が1回発生するたびに、軽微な事故はそれよりもはるかに多く発生し、無傷の事故はさらに頻繁に発生します。このグラフは、組織や施設が重大な事故を予防するためには、軽微な事故や無傷の事故にも注目し、それらを減少させる必要があることを強調しています。​

標本の平均の期待値（平均）

1. 標本の平均: 標本の平均は、あるデータセットや標本集合内のすべての値を合計し、その総和を標本のサイズ（データ数）で割った値です。これは、標本内のデータポイントの平均値を示します。
2. 期待値: 期待値は、確率論や統計学で用いられる概念で、ある事象が発生する確率を重みづけした平均です。期待値は、ランダムな試行の結果に関する平均的な値を示します。
3. 不偏推定量: 標本の平均の期待値は、母集団の平均と等しい性質があります。言い換えれば、標本の平均は、母集団の平均を推定するのに適した「不偏推定量」として機能します。不偏推定量は、推定値が母集団の真の値からバイアスを持たないことを示します。

ビジネスの応用例

ビジネスにおいて、標本の平均の期待値は以下のような場面で活用されます。

• 市場調査: 製品やサービスの市場調査において、ランダムに選ばれた標本から得られたデータを使用して、市場全体の平均額や嗜好を推定します。標本の平均は、母集団全体の平均に近い値を提供し、市場動向を理解するのに役立ちます。
• 顧客満足度調査: 顧客からのフィードバックを収集する際、ランダムに選ばれた標本を対象に調査を行います。この標本から得られた平均スコアは、顧客満足度の全体的な平均を推定するのに使用されます。

Pythonコード

sample = np.random.randn(100)
sample_mean = np.mean(sample)
print(sample_mean)

-0.11840291840664756

上記のPythonコードは、100個のランダムな数値からなる標本を生成し、その標本の平均を計算しています。この例では、標本の平均は-0.1184です。この標本の平均は、母集団の平均を推定するための一つの方法であり、不偏推定量として役立つことがあります。

import matplotlib.pyplot as plt

# Generate 1000 samples, each of size 100, from a standard normal distribution
samples = [np.random.randn(100) for _ in range(1000)]

# Calculate the mean of each sample
sample_means = [np.mean(sample) for sample in samples]

# Plot the histogram of the sample means
plt.hist(sample_means, bins=30, density=True, alpha=0.7, label='Sample Means', color='blue')

# Plot a vertical line for the population mean (which is 0 for a standard normal distribution)
plt.axvline(x=0, color='red', linestyle='dashed', linewidth=1, label='Population Mean')

# Add title and labels
plt.title('Distribution of Sample Means (n=100)')
plt.xlabel('Sample Mean')
plt.ylabel('Frequency')
plt.legend()

# Display the plot
plt.show()

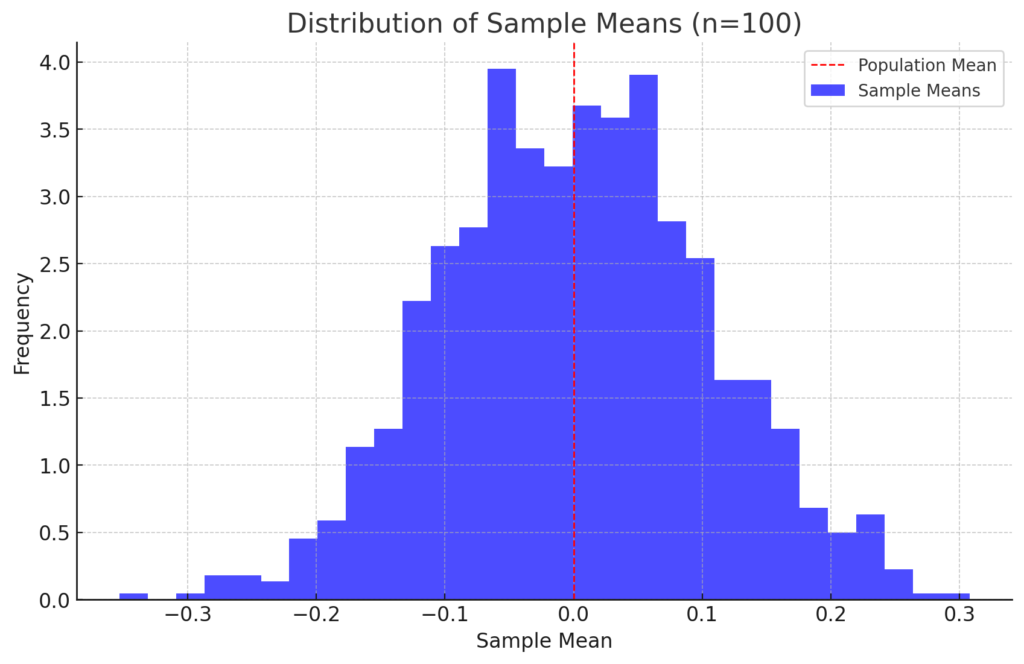
上記のヒストグラムは、標準正規分布から取得された100個のデータ点から成る1000の標本の平均を示しています。

• 青色のバーは、各標本の平均の分布を示しています。
• 赤色の破線は、母集団の平均（この場合は0）を示しています。

このヒストグラムから、標本の平均が母集団の平均（0）の周りに集まっていることがわかります。これは、大数の法則と中心極限定理の影響を示しています。標本の大きさが増えると、標本の平均は母集団の平均にさらに近づくことが期待されます。​

母集団と標本の関係

1. 母集団 (Population): 母集団は、研究対象となる全ての要素や個体の集合を指します。母集団は通常、ある特定の属性や性質に関連するすべての個体を含みます。例えば、ある国のすべての市民、ある会社のすべての製品、ある生態系内のすべての生物などが母集団と考えられます。
2. 標本 (Sample): 標本は、母集団からランダムまたは特定の方法で選ばれた一部の要素や個体の集合です。母集団の一部を標本として抽出することで、全体の特性や特徴を推測するためのデータを収集します。標本は通常、母集団の大きさに比べて小さなサイズであり、コストや時間を節約するために使用されます。

ビジネスの応用例

ビジネスにおける母集団と標本の関係の例を考えてみましょう。

• 市場調査: 新製品の市場性を調査する場合、全ての潜在的な顧客からのフィードバックを収集するのは非現実的な場合があります。代わりに、ランダムまたは戦略的に選ばれた一部の消費者を対象に調査を行います（標本）。この標本から収集されたデータを基に、全体の市場の反応や意見を予測し、新製品の戦略を決定します。
• 品質管理: 製造工程の品質を評価するために、製品の一部をランダムに抽出し、テストや検査を行います。この標本から得られた結果を基に、全体の生産ロットの品質を推測し、問題がある場合に対策を講じます。

Pythonコード

import numpy as np
# Generate population data
population = np.random.randn(10000)
# Sample from the population
sample = np.random.choice(population, size=500)
# Set print options to limit the number of elements displayed
np.set_printoptions(threshold=10)
# Print the sample
print(sample)

[-0.65727451  0.44973858  1.4236277  ... -1.08942994  0.64248421
 -1.30328544]

上記のPythonコードは、母集団と標本の関係を示す簡単な例です。まず、10000個のデータポイントからなる母集団データを生成します。次に、この母集団から500個のデータをランダムに抽出して標本を作成します。この標本は、母集団の一部を代表するものです。標本から得られたデータを分析することで、母集団全体に関する情報を推定できます。

標本の平均

1. 標本の平均: 標本の平均は、あるデータセットまたは標本集合内のすべての値の合計を、データの数（サンプルサイズ）で割った値です。標本の平均は、そのデータセット内の値の中央的な位置を示します。
2. 数学的表現: 標本の平均（標本平均）は、以下のような数学的な式で計算されます。 \[
   \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i
   \] ここで、\(\bar{X}\) は標本の平均、\(X_i\) は標本データの各値を表し、\(n\) は標本データの数を示します。具体的には、各データ点を合計し、その合計をデータ数で割って平均を求めます。

ビジネスの応用例

ビジネスにおいて、標本の平均は多くの場面で使用されます。

• 商品評価: 顧客から収集された商品の評価点数を考えてみましょう。たくさんの顧客からの評価がある場合、これらの評価点数の平均を計算することで、その商品の全体的な評価を把握できます。例えば、評価点数の平均が高ければ、商品の人気度や品質が高いと言えます。
• 顧客購入回数: ある期間内に顧客が何回商品を購入したかを記録する場合、顧客ごとに購入回数を集計し、その平均を計算することで、平均的な顧客の購買頻度を理解できます。これは、販売戦略や広告キャンペーンの最適化に役立ちます。

Pythonコード

import numpy as np
sample_data = np.array([3, 4, 5, 4, 3, 5, 4, 3])
sample_mean = np.mean(sample_data)
print(sample_mean)

3.875

上記のPythonコードは、標本データの平均を計算するシンプルな例です。与えられた標本データ [3, 4, 5, 4, 3, 5, 4, 3] の平均は 3.875 です。これは、この標本内のデータ値の平均を示しています。 Pythonを使用することで、標本の平均を迅速に計算し、データセットの中心的な傾向を理解するのに役立ちます。

標本の平均の分散

1. 標本の平均の分散: 標本の平均の分散は、標本平均のばらつきや不確実性を示す尺度です。標本データセット内の異なるサンプルを取った場合、そのサンプルの平均値がどれくらい異なるかを表します。つまり、標本平均のバラつきを評価するための指標です。
2. 数学的表現: 標本の平均の分散は、母集団の分散（\(\sigma^2\)）を標本サイズ（\(n\)）で割ったものとして計算されます。 \[
   \text{標本の平均の分散} = \frac{\sigma^2}{n}
   \] ここで、\(\sigma^2\) は母集団の分散を表し、\(n\) は標本のサイズ（標本データの個数）です。

ビジネスの応用例

ビジネスにおいて、標本の平均の分散は以下のように応用されます。

• 品質管理: 製品の生産ラインでの品質管理において、標本データを使用して異なる時点での標本平均のばらつきを評価します。例えば、ある製品の寸法を測定し、異なる日に異なる標本を取って測定すると、その標本平均値がどれくらいばらつくかを分散を通じて評価できます。これは生産プロセスの一貫性を評価し、品質管理の向上に役立ちます。

Pythonコード

population_variance = np.var(sample_data, ddof=0)
sample_size = len(sample_data)
variance_of_sample_mean = population_variance / sample_size
print(variance_of_sample_mean)

0.076171875

上記のPythonコードは、標本の平均の分散を計算するシンプルな例です。与えられたデータセットの分散を計算し、それを標本サイズで割ることで、標本平均の分散を求めます。この分散は、標本平均のばらつきを示し、異なる標本から得られる平均値がどれくらい異なるかを評価するのに役立ちます。

標本分散と不偏（標本）分散

1. 標本分散: 標本分散は、標本内のデータポイントがどれくらい平均からばらついているかを示す尺度です。具体的には、各データポイントと標本平均との差の2乗を合計し、それを標本サイズで割ったものです。数学的には、以下の式で表されます。 \[
   \text{標本分散} = \frac{1}{n}\sum_{i=1}^{n} (X_i – \bar{X})^2
   \] ここで、\(\text{標本分散}\) は標本の分散、\(X_i\) は各標本データの値、\(\bar{X}\) は標本の平均、\(n\) は標本サイズです。
2. 不偏分散: 標本分散にはバイアスがあるため、不偏分散が導入されました。標本分散は、母分散よりも小さくなる傾向があります。不偏分散はこのバイアスを補正した分散です。不偏分散は、標本分散を計算した結果に補正項 \(\frac{1}{n-1}\) を掛けることで計算されます。 \[
   \text{不偏分散} = \frac{1}{n-1}\sum_{i=1}^{n} (X_i – \bar{X})^2
   \] ここで、\(\text{不偏分散}\) は不偏の分散、\(X_i\) は各標本データの値、\(\bar{X}\) は標本の平均、\(n\) は標本サイズです。

ビジネスの応用例

ビジネスにおいて、標本分散と不偏分散はデータのばらつきを評価する際に使用されます。

• 市場調査: 市場調査において、顧客の意見や評価のばらつきを評価するために不偏分散が使用されます。これにより、市場全体の評価の正確なばらつきを把握し、意思決定に役立ちます。
• 品質管理: 製品の品質管理において、不偏分散は製品の特定の属性や寸法のばらつきを評価するために使用されます。これにより、生産プロセスの品質コントロールを向上させます。

Pythonコード

sample_variance = np.var(sample_data, ddof=0)
unbiased_variance = np.var(sample_data, ddof=1)
print(unbiased_variance)

0.6964285714285714

上記のPythonコードは、標本分散と不偏分散を計算する例です。np.var 関数を使用して、データの分散を計算します。 ddof パラメータを設定することで、不偏分散を計算できます。不偏分散の方が、標本のばらつきをより正確に評価します。

大数の法則

1. 大数の法則: 大数の法則は、統計学の基本原則の一つで、標本サイズ（データ数）が大きくなるにつれて、標本から計算した平均値（標本平均）が母集団の平均に収束するという法則です。つまり、データを十分に多く収集すると、統計的に得られた平均値は真の平均にとても近づくとされています。
2. 数学的表現: 大数の法則は、以下のように数学的に表現されます。\(X_1, X_2, \ldots, X_n\) が同じ確率分布に従う独立なランダム変数である場合、 \[
   \lim_{{n \to \infty}} \frac{X_1 + X_2 + \ldots + X_n}{n} = \text{母集団の平均}
   \] という式が成り立ちます。ここで、\(n\) は標本サイズを表します。

ビジネスの応用例

ビジネスにおいて、大数の法則は以下のように応用されます。

• データ分析: 顧客の購買履歴やユーザーの行動ログなど、大規模なデータセットを収集し、それに基づいてビジネス戦略を策定する場合、大数の法則がとても重要です。データの量が増えるほど、統計的な解析結果が信頼性を持ち、真の傾向やパターンに近づくことを示唆しています。この法則を理解することで、データ分析の信頼性を評価し、意思決定に信頼性を持たせることができます。
• 市場調査: 市場調査においても、大数の法則が重要です。多くの顧客や消費者からのデータを収集し、市場動向を把握する場合、データの量が増えることで正確な市場トレンドを捉えることができます。この法則に基づいて、市場調査のサンプルサイズを決定できます。

大数の法則は、データ収集と分析において、十分なデータ量が信頼性の高い結果を得るために不可欠な原則です。

Pythonコード

# The law of large numbers is a theoretical concept and doesn't have a direct code implementation.

中心極限定理

1. 中心極限定理: 中心極限定理は、統計学の重要な法則の一つで、母集団の分布がどのようであっても、標本サイズが大きい場合において、標本平均の分布が正規分布に近似するという法則です。言い換えれば、多くのランダムな標本を抽出し、それぞれの標本の平均を計算すると、その平均値たちの分布が正規分布に従うことが期待されます。
2. 数学的表現: 中心極限定理は、次のように表現されます。(X_1, X_2, \ldots, X_n) が同じ分布に従う独立なランダム変数である場合、(n) 個のサンプルからなる標本の平均 (\bar{X}) の分布は、標本サイズ (n) が大きくなるにつれて、正規分布に収束する。

ビジネスの応用例

ビジネスにおいて、中心極限定理は以下のように応用されます。

• データ分析: 大規模なデータセットが利用可能なビジネスシナリオ（例：eコマースの購入履歴、ウェブトラフィックデータ）では、中心極限定理が重要です。標本の平均を用いて母集団の特性を推測する場合、標本サイズが大きいと、標本平均の分布が正規分布に近似し、統計的な推測が容易になります。これにより、売上予測、広告効果の評価、顧客行動の分析などの重要なビジネス問題を解決できます。
• 信頼性評価: 大量のデータからの情報をもとに意思決定を行う場合、中心極限定理に基づいて、標本の平均や統計的指標の信頼性を評価します。正規分布に従う分布を仮定することが多いため、中心極限定理はビジネスの意思決定においてとても有用です

Pythonコード

sample_means = [np.mean(np.random.choice(sample_data, size=50)) for _ in range(1000)]
plt.hist(sample_means, bins=30)
plt.title("Distribution of Sample Means")
plt.show()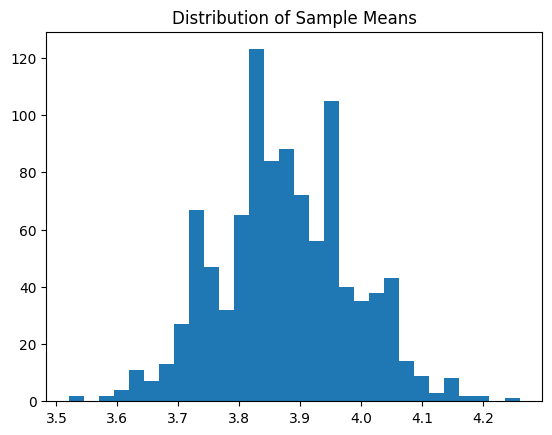

上記のPythonコードは、中心極限定理を視覚的に示すものです。多くのランダムな標本を抽出し、それぞれの標本の平均を計算して分布を描画することで、中心極限定理の概念を視覚的に理解できます。

標本平均から母平均を推定する

1. 標本平均: 標本平均は、あるデータセット内のすべての値の合計を、データ点の数で割った値です。つまり、標本データ内の平均値を示します。標本平均は、そのデータセット内での平均的な値を表しますが、これが母集団全体の平均であるかは確定的ではありません。
2. 母平均を推定: 標本平均は、母集団の平均（母平均）を推定するために使用されます。大前提は、標本が母集団を代表してランダムに選ばれたものであることです。もし標本がランダムでかつ十分に大きい場合、標本平均は母平均にとても近い推定値となります。このため、母平均を正確に知らなくても、標本平均を用いて母平均を推定できます。

ビジネスの応用例

ビジネスにおいて、標本平均から母平均を推定するのは以下のように応用されます。

• 品質管理: 製品の品質を評価するために、ランダムに選ばれた一部の製品（標本）をテストします。テスト結果から、その標本の品質を評価し、さらに標本平均を使用して全体の製品の品質を推定します。母平均の推定を通じて、製品の全体的な品質状態を把握し、必要に応じて改善できます。
• 市場調査: 市場調査において、消費者の意見や評価を調査するためにサンプルを取ります。これらのサンプルデータから標本平均を計算し、それを基に母集団全体の意見や傾向を推定します。これにより、市場全体の評判や需要を理解し、ビジネス戦略を調整するのに役立ちます。

Pythonコード

import numpy as np
sample_data = np.array([3, 4, 5, 4, 3, 5, 4, 3])
estimated_population_mean = np.mean(sample_data)
print(estimated_population_mean)

3.875

上記のPythonコードは、データセットから標本平均を計算し、その結果を母平均の推定値として示しています。データの平均値を求めることで、データの中心的な傾向を理解し、母集団全体に関する洞察を得る手助けとなります。

仮説検定

仮説検定は、統計学の手法の一つで、ある仮説（帰無仮説）が正しいかどうかを統計的に評価するために使用されます。帰無仮説は通常、何らかの仮定や既存の状態を表し、それを検証するための手段として仮説検定が利用されます。一般的に、帰無仮説は「何も効果がない」または「2つのグループは同じである」といった主張を含みます。

仮説検定の手順は以下の通りです。

• ステップ 1: 帰無仮説（H0）と対立仮説（H1）を設定します。帰無仮説は通常、何も変化がないという主張を示し、対立仮説は何かが変化したという主張を示します。
• ステップ 2: 検定統計量（例：t値、z値など）を計算します。この統計量は、データから得られます。
• ステップ 3: 検定統計量を評価し、帰無仮説が正しい場合に得られる確率（p値）を計算します。p値は、帰無仮説が正しいと仮定した場合に、観測されたデータよりも極端な結果が得られる確率です。
• ステップ 4: p値を事前に設定した有意水準と比較し、帰無仮説を受け入れるか棄却するかを決定します。通常、有意水準は0.05または0.01などが使用されます。p値が有意水準よりも小さい場合、帰無仮説は棄却され、対立仮説が受け入れられます。

ビジネスの応用例

ビジネスにおける仮説検定の例は次の通りです。

• 販売促進効果の評価: 新製品の販売促進策が、既存の方法に比べて売上に効果があるかを検証するために仮説検定を使用します。帰無仮説は「販売促進策は効果がない」という主張であり、対立仮説は「販売促進策は効果がある」という主張です。実施された実験データから計算された検定統計量とp値を用いて、促進策の効果を統計的に評価します。
• 製品の品質管理: 製品の品質が一定であることを確認するために、製品のサンプルを検査する場合があります。帰無仮説は「品質に変化がない」とし、対立仮説は「品質に変化がある」とします。検査結果から検定統計量を計算し、品質に変化があるかを統計的に評価します。

Pythonコード

from scipy.stats import ttest_ind
group_a = np.array([3, 4, 5, 4, 3])
group_b = np.array([5, 6, 7, 5, 6])
t_stat, p_val = ttest_ind(group_a, group_b)
print(t_stat)
print(p_val)

-3.7796447300922726
0.005390882019515592

上記のPythonコードは、2つのグループ間で平均値の差を評価するt検定を示しています。この例では、2つのグループのデータから計算されたt値とp値を使用して、2つのグループ間の統計的な差異を評価しています。

二標本問題を1つの確率変数で扱う

1. 二標本問題: 二標本問題は、通常、2つの異なるグループ（例：広告キャンペーンAと広告キャンペーンBのクリック数）を比較する統計的な問題です。これらのグループの平均値や効果の差異を評価することが一般的です。
2. 1つの確率変数: 2つの異なるグループを1つの確率変数として扱うために、差を取ることが考えられます。具体的には、グループAからグループBの値を引くことで、各データポイントの差を得ます。これにより、2つのグループのデータを1つのデータセットとして扱うことができます。

ビジネスの応用例

ビジネスにおける二標本問題を1つの確率変数として扱う例は以下の通りです。

• 広告キャンペーンの効果比較: 広告主は2つの広告キャンペーン（AとB）を実施し、それぞれのクリック数を収集しました。これらのデータを比較して、どちらの広告キャンペーンが効果的かを判断したいとします。この場合、クリック数の差を計算し、その差の平均や統計的な特性を評価します。差の平均が正であれば、キャンペーンAの方が良い効果があると結論付けることができます。

Pythonコード

difference = group_a - group_b
mean_difference = np.mean(difference)
print(mean_difference)

-2.0

上記のPythonコードでは、2つのグループ（group_aとgroup_b）のデータからクリック数の差を計算し、その差の平均を求めています。差の平均が正または負であるかによって、2つのグループ間での効果の大きさを評価できます。この例では、差の平均が-2.0という結果が得られました。これは、グループBの方が平均的に2.0クリック多いことを示唆しています。

\(X^2\)分布と適合度検定

1. \(X^2\)分布: \(X^2\)分布（カイ二乗分布）は、独立した確率変数の二乗和が従う確率分布です。通常、自由度（degrees of freedom）と呼ばれるパラメータに依存します。自由度が大きくなるにつれて、\(X^2\)分布は正規分布に近づきます。\(X^2\)分布は、確率統計学や仮説検定などの分野で広く使用されます。
2. 適合度検定: 適合度検定は、観測データが期待される分布に適合しているかどうかを評価するための統計的な手法です。具体的には、観測データと期待される理論的な分布（例：一様分布、正規分布など）との間で統計的な適合度を検証します。適合度検定は、観測データと期待値が統計的に有意に異なる場合に、データが予想される分布に適合していないことを示すのに役立ちます。

ビジネスの応用例

ビジネスにおける適合度検定の例は以下の通りです。

• 製品の不良率の評価: 製造プロセスから得られた製品の不良率データを持っていると仮定しましょう。このデータが期待される不良率と一致しているかどうかを確認するために、適合度検定を使用します。期待される不良率を仮定し、実際の不良率データと比較して、統計的な適合度を評価します。もしデータが期待値から統計的に有意に異なる場合、製品の不良率が期待通りでない可能性があります。

Pythonコード

from scipy.stats import chisquare
observed = np.array([10, 20, 30])
expected = np.array([15, 15, 30])
chi2_val, p_val = chisquare(observed, expected)
print(chi2_val)
print(p_val)

3.3333333333333335
0.1888756028375618

上記のPythonコードでは、適合度検定の例が示されています。observedは観測データで、expectedは期待される理論的な分布を表します。chisquare関数を使用して、観測データと期待値を比較し、適合度検定の結果である\(X^2\)値とp値を計算します。p値が小さい場合、観測データが期待値と統計的に有意に異なることを示唆します。この例では、p値が0.1889であるため、観測データが期待値から統計的に有意に異なるとは言えないと結論付けられます。

ガンマ関数

1. ガンマ関数: ガンマ関数（Gamma function）は、階乗の概念を実数全体に拡張した特殊な数学的関数です。階乗は自然数に対して定義されており、\(n\) の階乗は\(n!\)と表されます。一方、ガンマ関数は自然数以外の実数に対しても定義され、一般的に\(\Gamma(x)\)と表されます。ガンマ関数は次のように表現できます。 \(\Gamma(x) = \int_{0}^{\infty} t^{x-1} e^{-t} dt\) ここで、\(x\)は実数です。ガンマ関数は統計学や確率論、物理学など多くの分野で使用され、特に確率分布の形状をモデル化するために利用されます。

ビジネスの応用例

ビジネスにおけるガンマ関数の例は以下の通りです。

• 製品の生存期間モデリング: 製品の寿命や生存期間をモデル化する場合、ガンマ分布が頻繁に使用されます。ガンマ関数は、製品が特定の期間で故障する確率分布を表現するのに役立ちます。例えば、製品の寿命が平均的にどれくらいであるかや、信頼性の評価に使用されます。

Pythonコード

from scipy.special import gamma
value = 4.5
result = gamma(value)
print(result)

11.63172839656745

上記のPythonコードでは、ガンマ関数の計算例が示されています。gamma関数を使用して、ガンマ関数の値を計算しています。この例では、\(x\)の値が4.5で、計算結果が11.63となっています。これは、\(\Gamma(4.5)\)の値を表しています。

\(X^2\)分布

\(X^2\)分布: \(X^2\)分布（カイ二乗分布）は、正規分布に従う独立した確率変数の二乗和が従う確率分布です。\(X^2\)分布は、通常、自由度（degrees of freedom）と呼ばれるパラメータに依存します。自由度は、分布の形状を決定する重要な要素で、自由度が大きくなるにつれて分布はより正規分布に近づきます。

ビジネスの応用例

\(X^2\)分布は、ビジネスや産業のさまざまな側面で使用されます。特に、製品の品質管理やデータの適合度検定などの分野で役立ちます。たとえば、製品の返品率が予想と一致しているかどうかを確認するために、適合度検定で\(X^2\)分布が使用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
df = 4  # 自由度
x = np.linspace(chi2.ppf(0.01, df), chi2.ppf(0.99, df), 100)
plt.plot(x, chi2.pdf(x, df))
plt.title('Chi-square Distribution with 4 degrees of freedom')
plt.show()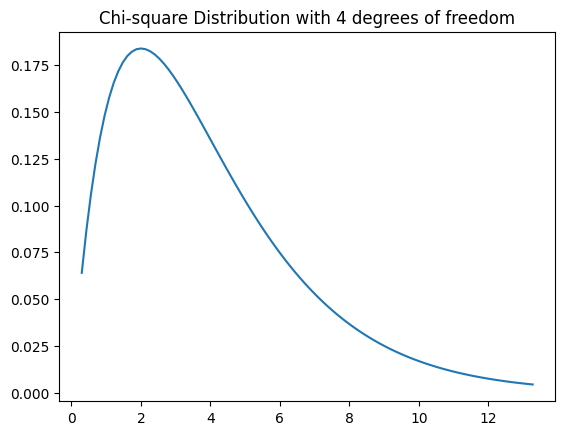

上記のPythonコードでは、\(X^2\)分布を可視化しています。具体的には、自由度が4の\(X^2\)分布を示しています。これは、確率密度関数（PDF）を用いて分布を描画しています。自由度が4の場合、\(X^2\)分布はピークが4付近にあり、分散が大きい分布となります。

このような可視化は、統計的な分析や仮説検定において、\(X^2\)分布の性質や特性を理解するのに役立ちます。

正規分布の\(X^2\)分布

正規分布に従う独立な確率変数の二乗の和は、\(X^2\)分布（カイ二乗分布）に従います。これは、正規分布から得られるランダムな値を取り、それらの値を二乗し、その和を取る操作を考えると理解しやすいです。\(X^2\)分布は、通常、自由度（degrees of freedom）と呼ばれるパラメータに依存します。自由度は、この分布の形状を決定します。

ビジネスの応用例

正規分布の\(X^2\)分布は、品質管理や統計的な分析など多くのビジネス応用で役立ちます。例えば、二つの製品の品質テストの結果の分散を比較する場合、各製品のテスト結果が正規分布に従っていると仮定し、その分散を計算して比較します。\(X^2\)分布は、この比較に使用されます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
# Generate a sample from a normal distribution
normal_sample = np.random.normal(size=1000)
# Calculate the sum of squares of the sample
chi_square_val = np.sum(normal_sample**2)
# Create a histogram of the sample
plt.hist(normal_sample, bins=20, density=True, alpha=0.6, color='g', label='Normal Distribution')
# Set labels and title in English
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Histogram of Normal Distribution Sample')
# Display the calculated chi-square value in English
plt.text(2, 0.25, f'Chi-square value: {chi_square_val:.2f}', fontsize=12, color='r')
# Show the legend
plt.legend()
# Show the plot
plt.show()

上記のPythonコードでは、正規分布に従うランダムなデータを生成し、そのデータの二乗の和を\(X^2\)分布の性質に基づいて計算しています。また、データのヒストグラムを描画し、\(X^2\)分布の特性を可視化しています。この例では、正規分布のサンプルを生成し、それらの値を二乗し、その和を計算しています。そして、計算された\(X^2\)値をヒストグラムとして表示しています。このプロットを通じて、正規分布の\(X^2\)分布における性質を理解するのに役立ちます。

自由度2以上の\(X^2\)分布

自由度2以上の\(X^2\)分布（カイ二乗分布）は、2つ以上の正規分布に従う独立な確率変数の二乗の和の確率分布です。自由度（degrees of freedom）は、この分布の形状を決定する重要なパラメータで、自由度が増加すると分布はより正規分布に近づきます。

ビジネスの応用例

自由度2以上の\(X^2\)分布は、ビジネスや品質管理の分野で使用されます。例えば、複数の製品ラインの品質テストの結果を統合して、全体の品質を評価する場合に役立ちます。各ラインのテスト結果が正規分布に従うと仮定し、それらの結果を結合して全体の品質を評価するために使用されます。

Pythonコード

df = 5
x = np.linspace(chi2.ppf(0.01, df), chi2.ppf(0.99, df), 100)
plt.plot(x, chi2.pdf(x, df))
plt.title('Chi-square Distribution with 5 degrees of freedom')
plt.show()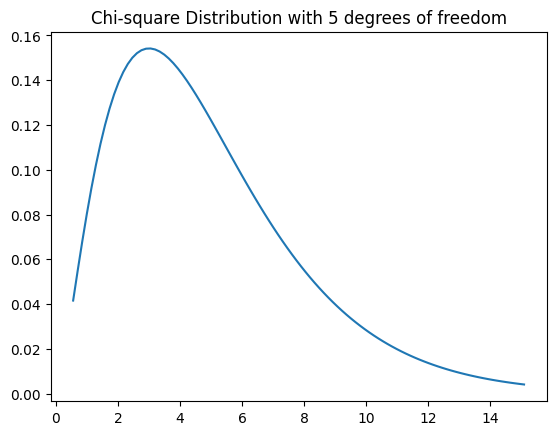

上記のPythonコードでは、自由度が5の\(X^2\)分布を可視化しています。自由度が5の場合、\(X^2\)分布は正規分布に近い形状を持ちます。プロットには、確率密度関数（PDF）が表示され、自由度が増加すると分布がより正規分布に近づくことがわかります。このような可視化は、統計的な分析や品質評価において、\(X^2\)分布の性質を理解するのに役立ちます。

\(X^2\)分布の組み込み関数

Pythonのscipy.statsモジュールには、統計的な計算や確率分布に関する多くの組み込み関数が含まれています。その中には、\(X^2\)分布に関する計算を行うための関数も含まれています。これには、確率密度関数（PDF）、累積分布関数（CDF）、パーセントポイント関数（PPF）などが含まれます。

ビジネスの応用例

組み込み関数を使用する主なビジネスの応用例は、品質管理や適合度検定です。たとえば、製品の不良率が特定の閾値を超えているかどうかを評価するために、\(X^2\)分布の累積分布関数を使用することがあります。累積分布関数は、特定の値以下の確率を計算するのに役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
df = 3  # 自由度を設定
x = np.linspace(0, 10, 400)  # x軸の範囲を設定
y = chi2.cdf(x, df)  # 累積分布関数を計算
plt.plot(x, y)
plt.title(f'Chi-squared CDF with df={df}')
plt.xlabel('x')
plt.ylabel('CDF')
plt.grid(True)
plt.show()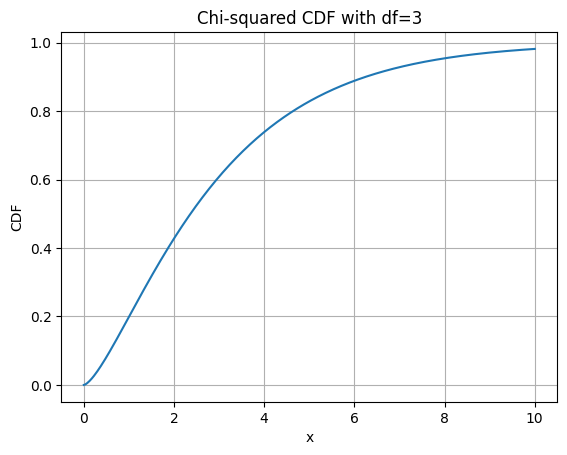

上記のPythonコードでは、自由度が3の\(X^2\)分布の累積分布関数（CDF）を計算し、その結果をグラフ化しています。このグラフは、累積分布関数の値がx軸に対してどのように変化するかを示しています。自由度が3の場合、CDFの値はx軸が増加するにつれて増加し、確率が積み重なっていく様子がわかります。このようなグラフを用いて、確率分布の性質を視覚的に理解できます。

標本分散の\(X^2\)分布

正規分布に従うデータの標本分散は、\(X^2\)分布（カイ二乗分布）と関連があります。具体的には、標本サイズを\(n\)としたとき、\((n-1) \times\)標本分散 / 母分散 は、自由度 \(n-1\) の\(X^2\)分布に従います。

ビジネスの応用例

標本分散の\(X^2\)分布は、品質管理やプロセスの安定性の評価などのビジネスアプリケーションで使用されます。例えば、製品の製造プロセスが安定しているかどうかを確認するために、標本分散の分布を評価することがあります。この分布を用いて、観測された標本分散が母分散とどの程度一致しているかを評価できます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
sample_data = np.array([2.3, 2.9, 3.1, 2.8, 3.0])
n = len(sample_data)
sample_variance = np.var(sample_data, ddof=1)
scaled_variance = (n-1) * sample_variance  # This follows chi-square distribution with n-1 df
# Generate x values for the chi-square distribution
x = np.linspace(0, 20, 1000)
# Calculate the probability density function (PDF) of the chi-square distribution
pdf = chi2.pdf(x, df=n-1)
# Create a plot of the chi-square distribution
plt.figure(figsize=(8, 6))
plt.plot(x, pdf, 'r-', label='Chi-square Distribution (df=n-1)')
plt.fill_between(x, pdf, where=(x >= scaled_variance), color='gray', alpha=0.5, label='Area under Chi-square')
plt.axvline(x=scaled_variance, color='b', linestyle='--', label='Scaled Variance')
plt.xlabel('Chi-square Value')
plt.ylabel('Probability Density')
plt.title('Chi-square Distribution vs. Scaled Variance')
plt.legend()
plt.grid(True)
# Show the plot
plt.show()

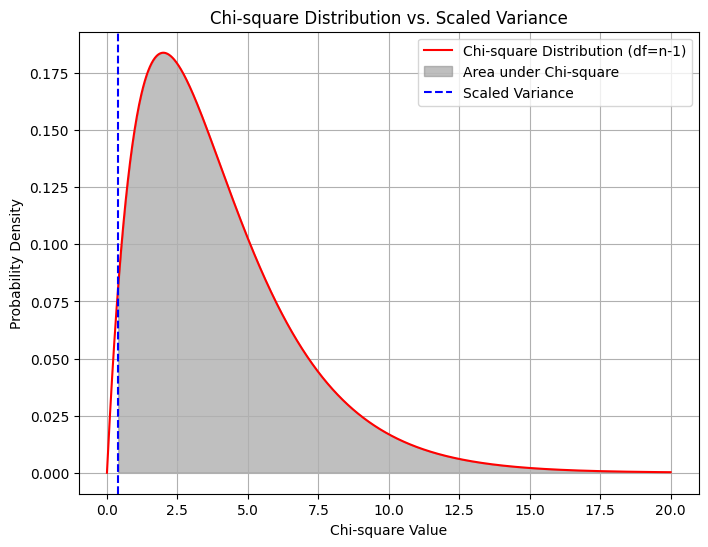
上記のPythonコードでは、与えられた標本データから標本分散を計算し、その分散値を自由度 \(n-1\) の\(X^2\)分布と比較しています。具体的には、\(X^2\)分布の確率密度関数（PDF）をプロットし、その下に標本分散のスケール変動を示しています。スケール変動は、\(X^2\)分布のどの領域に位置しているかを示しており、この領域内の確率を計算できます。これにより、標本分散が母分散と一致しているかどうかを統計的に評価するのに役立ちます。

メンデルの法則

メンデルの法則は、遺伝の基本的な法則であり、遺伝子の伝達パターンを説明します。具体的には、一対の対立遺伝子の分離（分離の法則）と異なる対の対立遺伝子の独立な組み合わせ（独立の法則）に関する2つの主要な法則が含まれます。

1. 分離の法則（Mendel’s Law of Segregation）: この法則によれば、各親から受け継ぐ遺伝子は、子孫に対して分離し、それぞれが異なる性質を持つ子孫を形成します。例えば、親の1つが青い花の遺伝子を持ち、もう1つが赤い花の遺伝子を持つ場合、子孫の花には青い花と赤い花が均等に現れます。
2. 独立の法則（Mendel’s Law of Independent Assortment）: この法則によれば、複数の遺伝的特性は互いに独立して遺伝子の組み合わせが形成されます。例えば、花の色と花の形状という2つの特性が独立して遺伝される場合、花の色が青である子孫でも花の形状は自由に組み合わさります。つまり、花の色が青い場合でも、その子孫には異なる花の形状が現れる可能性があります。

ビジネスの応用例

メンデルの法則は、農業や品種改良の分野で広く応用されています。具体的な例として、遺伝子組み換え作物の研究が挙げられます。農業業界では、特定の遺伝的特性を持つ新しい品種を開発するためにメンデルの法則を参考にし、希望する特性を持つ作物を効果的に育てることが目的です。メンデルの法則は、遺伝学的な情報を用いて効果的な品種改良を行うための基本的な原則としてとても重要です。

適合度検定

適合度検定は、観測データと理論的な期待値との間で、統計的な適合度を評価する統計テストの手法です。主にカテゴリカルデータ（例：カテゴリごとの頻度、割合など）の分布が、理論的な期待値や予測される分布とどれくらい一致しているかを確認するのに使用されます。

ビジネスの応用例

市場調査を通じて得られた製品の好みの分布と、予測モデルによる予測との間の適合度を評価するために使用できます。

1. 市場調査: 市場調査を通じて得られたデータ（例：消費者の好みや購買行動）が、事前に仮定された分布や予測モデルに一致しているかどうかを評価するために使用できます。たとえば、消費者が特定の製品カテゴリで購買する頻度が、予測モデルと一致しているかどうかを確認するために適合度検定を実施します。
2. 品質管理: 製品の品質テストの結果をカテゴリに分類し、期待される分布との適合度を確認することによって、製品の品質が標準に合致しているかどうかを評価します。品質が期待通りでない場合、製造プロセスの改善が必要です。

Pythonコード

import matplotlib.pyplot as plt
from scipy.stats import chisquare
observed = [50, 30, 20]
expected = [40, 40, 20]
chi2_stat, p_val = chisquare(observed, f_exp=expected)
# Create a bar chart to visualize observed and expected values
categories = ['Category 1', 'Category 2', 'Category 3']
plt.bar(categories, observed, label='Observed')
plt.bar(categories, expected, alpha=0.5, label='Expected')
plt.xlabel('Categories')
plt.ylabel('Counts')
plt.title('Observed vs. Expected Counts')
plt.legend()
# Display the chi-squared statistic and p-value as text on the plot
plt.text(0.5, 60, f'Chi-squared Statistic: {chi2_stat:.2f}', fontsize=12)
plt.text(0.5, 55, f'p-value: {p_val:.4f}', fontsize=12)
# Show the plot
plt.show()

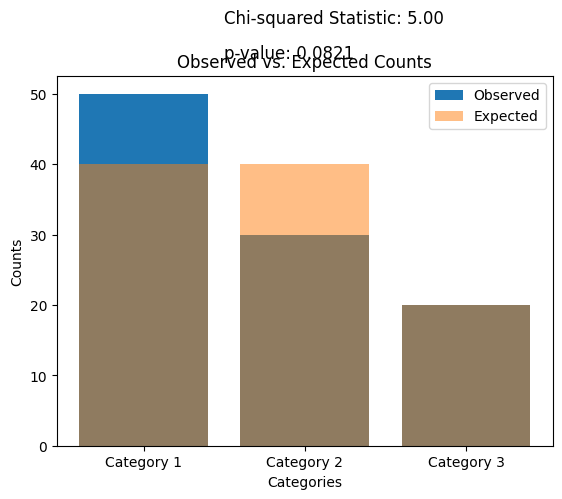
上記のPythonコードでは、適合度検定の一例として、観測された値と期待値を比較し、カイ二乗統計量とp値を計算しています。そして、観測値と期待値を可視化するために棒グラフを使用しています。検定の結果として、カイ二乗統計量とp値が表示されます。

ピアソン

カール・ピアソンは統計学者で、彼に因んで名付けられた統計的手法や指標が多く存在します。その中で、最もよく知られているのが「ピアソンの積率相関係数」です。この係数は、2つの量的変数間の線形関係の強度を測定するために使用されます。具体的には、2つの変数の値がどれだけ一緒に変化するかを示します。相関係数は、-1から1の範囲で表され、以下のように解釈できます。

• 1に近い場合: 強い正の相関（変数が一緒に増加する傾向が強い）
• -1に近い場合: 強い負の相関（変数が逆に関連して増減する傾向が強い）
• 0に近い場合: 相関がほとんどない（変数間の関連性が弱い）

ビジネスの応用例

ピアソンの相関係数は、ビジネス分野でさまざまな用途に使用されます。

1. 市場分析: 製品の価格と売上、広告費と売上、顧客の年齢と購買額など、異なる変数間の相関を評価して、戦略的な意思決定を行います。たとえば、価格と売上の間に強い正の相関があれば、価格を上げることで売上を増やす可能性があります。
2. リスク評価: 投資ポートフォリオ内の異なる資産クラス間の相関を評価して、リスクを分散する戦略を立てます。相関が低い資産クラスを組み合わせることで、リスクの低減が可能です。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 5, 6])
correlation_coefficient = np.corrcoef(x, y)[0, 1]
# Create a scatter plot to visualize the relationship between x and y
plt.scatter(x, y, label='Data Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Scatter Plot of x vs. y')
plt.legend()
# Display the correlation coefficient as text on the plot
plt.text(1, 5, f'Correlation Coefficient: {correlation_coefficient:.2f}', fontsize=12, color='r')
# Show the plot
plt.show()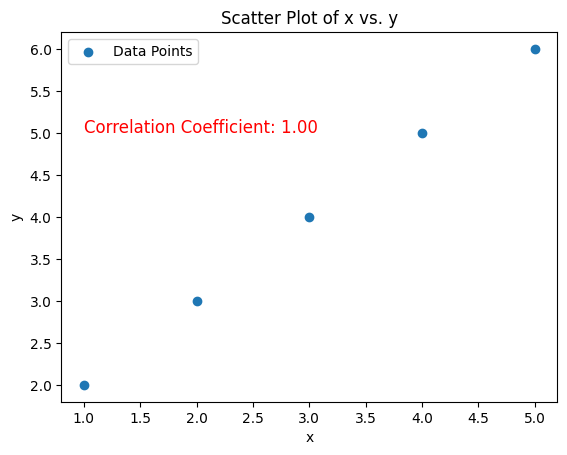

上記のPythonコードでは、2つの変数 x と y のデータポイントを散布図として表示し、np.corrcoef関数を使用して相関係数を計算しています。計算結果をグラフに表示し、相関係数の値をテキストとして表示しています。このようにして、2つの変数間の関係性を視覚化し、数値で評価できます。

t分布

t分布は、統計学で使用される確率分布の一つで、主にサンプルサイズが小さい場合の平均値の推定に関連しています。正規分布に従う母集団から無作為にサンプルを抽出し、そのサンプルの平均値を使って母集団の平均値を推定する際に、t分布が使用されます。

t分布は通常、平均0、標準偏差1を持つ標準正規分布から導かれますが、サンプルサイズが小さい場合、t分布は正規分布よりも尾が広くなり、サンプルサイズが大きくなると正規分布に近づきます。

ビジネスの応用例

1. 製品比較: 2つの異なる製品、広告、または戦略の効果を比較するためにt検定を使用します。たとえば、新しい広告戦略が従来の広告戦略と比較して売上に影響を与えているかどうかを評価するためにt検定が使用されます。
2. 品質管理: 製品の品質管理プロセスを監視し、異常を検出するためにt分布を使用します。品質が一定であることを確認し、問題を解決するための行動を決定するのに役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
df = 10  # 自由度
t_values = np.linspace(-3, 3, 1000)  # t-値の範囲を設定
probabilities = t.cdf(t_values, df)
# 特定のt-valueを設定
t_value = 2.0  # 例として2.0に設定
# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(t_values, probabilities, label=f't-distribution (df={df})')
plt.xlabel('t-value')
plt.ylabel('Probability')
plt.title(f'Cumulative Distribution Function (CDF) of t-distribution (df={df})')
plt.legend()
plt.grid(True)
# 特定のt-valueの確率を表示
plt.axvline(x=t_value, color='r', linestyle='--', label=f'Probability at t={t_value:.2f}')
plt.legend()
# Show the plot
plt.show()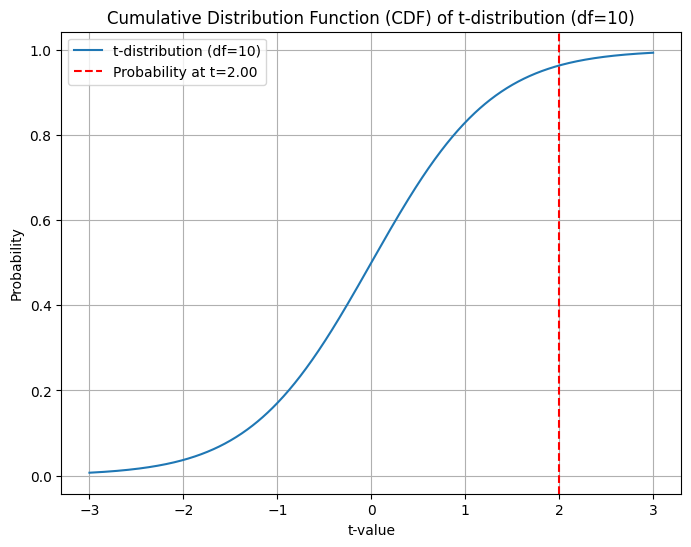

上記のPythonコードでは、t分布の累積分布関数（CDF）をグラフに表示しています。特定のt-値（t_value）の位置での確率を強調表示し、その確率を視覚的に理解できるようにしています。このように、t分布を理解し、その確率を評価するのに役立つツールです。

回帰分析の相関係数の妥当性にt分布を使う

回帰分析において、2つの変数間の相関係数を計算することが一般的です。この相関係数は、2つの変数間の線形関係の強さを示します。しかし、計算された相関係数が実際に統計的に有意であるかを評価する必要があります。この評価には、t分布を使用します。

具体的には、以下の手順で妥当性を評価します。

1. 相関係数の計算: まず、回帰分析を実行し、2つの変数の相関係数を計算します。これは、変数間の関係を数値で示すものです。
2. t統計量の計算: 次に、相関係数をt統計量に変換します。この変換には、標本サイズ（データの個数）と相関係数の標準誤差が使用されます。
3. t検定: 計算されたt統計量をt分布の表を使用して評価します。このとき、帰無仮説（例：相関が0である）と対立仮説（例：相関が0でない）を設定します。計算されたt統計量がt分布のどの位置にあるかを確認し、帰無仮説を採択または棄却します。
4. 有意性レベル: 棄却の判断は、有意性レベル（通常は0.05または0.01）に基づいて行います。有意性レベルは、帰無仮説を棄却するためのしきい値を示します。

ビジネスの応用例

ビジネスの場面では、回帰分析を使用して広告費と売上のような変数間の関係を評価することがよくあります。計算された相関係数が0ではなく、統計的に有意である場合、広告費と売上の間に実際に意味のある関係があることが示されます。この情報は、広告戦略の最適化や予測に役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import linregress
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
slope, intercept, r_value, p_value, std_err = linregress(x, y)
# Create a scatter plot of the data points
plt.scatter(x, y, label='Data Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Scatter Plot of x vs. y')
# Plot the regression line using the calculated slope and intercept
regression_line = slope * x + intercept
plt.plot(x, regression_line, color='r', label='Regression Line')
# Display the regression statistics as text on the plot
plt.text(1, 4, f'Slope: {slope:.2f}', fontsize=12, color='b')
plt.text(1, 3.8, f'Intercept: {intercept:.2f}', fontsize=12, color='b')
plt.text(1, 3.6, f'R-squared: {r_value**2:.2f}', fontsize=12, color='b')
# Show the legend
plt.legend()
# Show the plot
plt.show()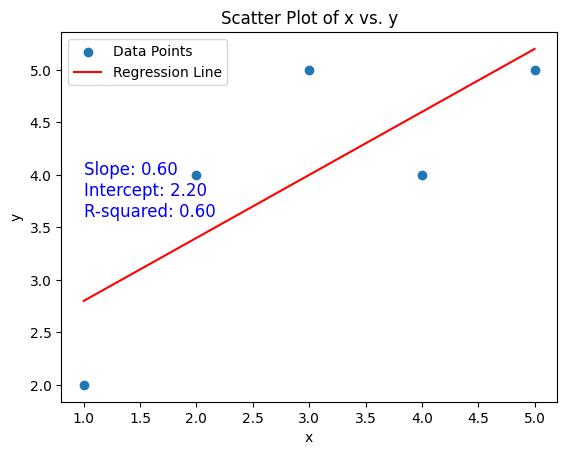

上記のPythonコードでは、2つの変数間の関係を示す回帰直線をプロットし、回帰統計情報（傾き、切片、R二乗値など）を表示しています。このようにして、計算された相関係数が統計的に有意であるかを評価する手助けを行います。

F分布

F分布は、2つのカイ二乗分布の比率から導出される確率分布です。F分布は、主に2つの標本分散の比をテストする際に使用されます。具体的には、2つの母集団の分散が等しいかどうかを比較するためにF検定が行われます。この検定は、統計的に2つの母集団の分散が異なる場合、または等しい場合の確率を評価します。

ビジネスの応用例

ビジネスの分野では、品質管理や製造プロセスの改善など、さまざまな場面でF検定が使用されます。以下は具体的な応用例です。

1. 製品品質管理: 製造プロセスにおける2つの異なる方法や装置の品質に関して、分散が等しいかどうかを確認するためにF検定を使用します。品質が等しい場合、より効率的な方法を採用できます。
2. 広告キャンペーンの効果測定: 2つの異なる広告キャンペーンの効果を比較する際、キャンペーン間の収益の分散が等しいかどうかを調べるためにF検定を適用することがあります。分散が等しい場合、どちらのキャンペーンも同様に効果的である可能性が高いです。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f
dfn, dfd = 5, 10  # 2つの自由度
f_values = np.linspace(0, 5, 1000)  # F-値の範囲を設定
probabilities = f.cdf(f_values, dfn, dfd)
# 特定のF-valueを設定
f_value = 2.0  # 例として2.0に設定
# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(f_values, probabilities, label=f'F-distribution (dfn={dfn}, dfd={dfd})')
plt.xlabel('F-value')
plt.ylabel('Probability')
plt.title(f'Cumulative Distribution Function (CDF) of F-distribution (dfn={dfn}, dfd={dfd})')
plt.legend()
plt.grid(True)
# 特定のF-valueの確率を表示
plt.axvline(x=f_value, color='r', linestyle='--', label=f'Probability at F={f_value:.2f}')
plt.legend()
# Show the plot
plt.show()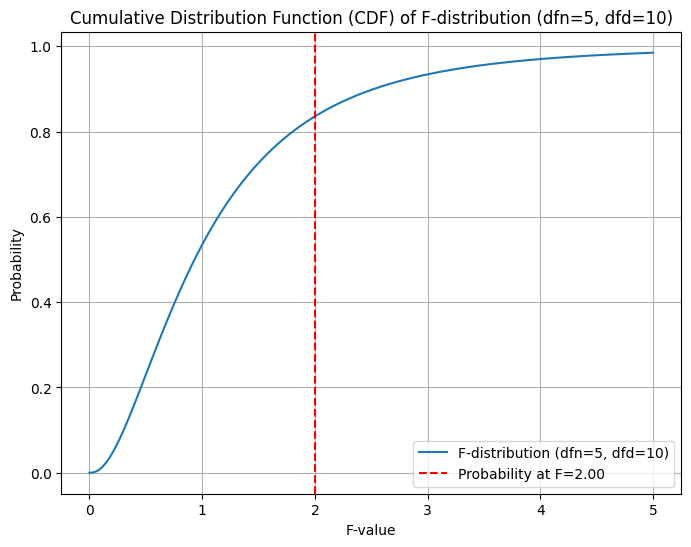

上記のPythonコードは、F分布の累積分布関数（CDF）を示しており、特定のF-値に対する確率を計算し可視化しています。このようにして、2つの分散を比較し、統計的な有意性を評価するためにF検定をサポートします。

フィッシャー

ロナルド・フィッシャーは、20世紀のイギリスの統計学者であり、遺伝学にも貢献した科学者です。彼は統計学の分野で多くの重要な貢献をし、その名前はいくつかの統計的手法に関連しています。特に、F分布やフィッシャーの正確な検定といった統計的手法が彼の名前にちなんで名付けられました。

ビジネスの応用例

フィッシャーの正確な検定は、ビジネスの分野でも有用です。以下はその一例です。

• 市場調査: 製品やサービスの好みを調査するための市場調査データがあり、2つのカテゴリ変数間の関連性を評価したい場合に、フィッシャーの正確な検定を使用できます。たとえば、2つの異なる製品の購買傾向が性別によって異なるかどうかを調査する際に利用されます。

Pythonコード

from scipy.stats import fisher_exact
table = [[8, 2], [1, 5]]
odds_ratio, p_value = fisher_exact(table)
print("Odds Ratio:", odds_ratio)
print("p-value:", p_value)

Odds Ratio: 20.0
p-value: 0.034965034965034975

上記のPythonコードは、Pythonのscipyライブラリを使用して、フィッシャーの正確な検定を実行する例です。この検定は、2×2のクロス表（コンティンジェンシーテーブル）を使用して、2つのカテゴリ変数間の関連性を評価します。検定の結果、オッズ比（Odds Ratio）とp値が得られ、カテゴリ変数間の関連性の有無を判断するのに役立ちます。

分散分析

分散分析（ANOVA）は、3つ以上の異なるグループまたは条件間で平均値の差を評価するための統計手法です。主に次の2つの種類があります。

1. 一元配置分散分析（One-Way ANOVA）: 1つの要因（説明変数）を持つ場合で、それを元に異なるグループ間の平均値の差を評価します。例えば、3つの異なる広告キャンペーンの効果を比較し、どのキャンペーンが最も効果的かを判断します。
2. 二元配置分散分析（Two-Way ANOVA）: 2つの要因（説明変数）を持つ場合で、それらの要因による平均値の差を評価します。例えば、製品の品質を改善するために、2つの異なる製造工程と3つの異なる材料の組み合わせが品質に与える影響を評価します。

ANOVAは、グループ間の平均値の差が偶然のものではなく、統計的に有意であるかを判断するのに役立ちます。ANOVAの結果として、F統計量（F-statistic）とp値（p-value）が得られ、統計的な有意性を評価します。有意な差がある場合、どのグループが異なるかを特定する追加の検定が行われることがあります。

ビジネスの応用例

ある企業が新しい製品を市場に投入し、その製品の広告キャンペーンを3つの異なる方法で実施したとします。企業は製品の成功を評価し、どの広告キャンペーンが最も売り上げを増やすのに効果的かを知りたいと考えています。この場合、分散分析（ANOVA）が役立ちます。

1. データ収集: 各広告キャンペーンの下での売り上げデータを収集します。つまり、広告キャンペーンA、B、Cの下での製品の売り上げを記録します。
2. 仮説設定: 仮説を設定します。例えば、「異なる広告キャンペーンには売り上げに影響を与える可能性がある」という仮説を立てます。
3. 分散分析の実行: 分散分析（ANOVA）を使用して、各広告キャンペーンの平均売り上げ間に統計的に有意な差があるかを評価します。
4. 結果の解釈: 分散分析の結果、p値が小さい場合、少なくとも2つの広告キャンペーンの間に統計的に有意な売り上げの違いがあることを示唆しています。この場合、どの広告キャンペーンが最も効果的かを特定するために追加の検定や比較ができます。
5. 意思決定: 統計的に有意な結果をもとに、最も効果的な広告キャンペーンを選択し、その方法を継続するか、他のキャンペーンに切り替えるかを決定します。

Pythonコード

import scipy.stats as stats
data1 = [2, 3, 4, 5, 2]
data2 = [6, 7, 8, 9, 5]
data3 = [10, 12, 11, 13, 15]
f_stat, p_value = stats.f_oneway(data1, data2, data3)
print("F-statistic:", f_stat)
print("p-value:", p_value)

F-statistic: 38.75949367088608
p-value: 5.802250999312677e-06

上記のPythonコードは、scipyライブラリを使用して一元配置分散分析（One-Way ANOVA）を実行する例です。異なる3つのデータセット（data1、data2、data3）の平均値の差を評価し、F統計量とp値を計算しています。p値が小さい場合、グループ間に統計的に有意な差がある可能性が高くなります。

確率母関数

確率母関数（Probability Generating Function、略してPGF）は、確率変数のすべての可能な値に対して、その値の確率を数学的に表現するための関数です。つまり、確率母関数は、ある確率分布に従う確率変数の確率分布を定義するのに使用されます。

確率母関数は、特に離散確率変数に関して利用されます。PGF は以下のように定義されます。

\[
G_X(z) = E(z^X) = \sum_{k=0}^{\infty} p_k z^k
\]

ここで、\( p_k \) は \( X = k \) となる確率を示します。

ビジネスの応用例

確率母関数はビジネスのさまざまな場面で使用できます。

1. 在庫の最適化: ある商品の需要が確率変数としてモデル化される場合、その需要の確率母関数を使用して、在庫レベルを最適化できます。確率母関数を利用して、需要の確率分布を把握し、在庫の補充タイミングや量を計算できます。
2. 需要予測: 製品の販売量や需要の予測に確率母関数を活用できます。製品の販売確率をモデル化し、将来の需要を予測する際に使用されます。これにより、需要の不確実性を考慮に入れた効果的な生産計画や資源割り当てが可能になります。
3. リスク評価: ビジネスプロジェクトや投資の成功確率を評価するためにも確率母関数が使用されます。プロジェクトの異なる結果の確率分布をモデル化し、リスクを評価するのに役立ちます。
4. 金融分野: 確率母関数は金融モデリングでも使用され、株価の変動やリスクの評価に役立ちます。将来の価格変動を確率分布としてモデル化し、ポートフォリオの最適化やオプション価格の評価に応用されます。

確率母関数は不確実性を扱うための重要なツールであり、さまざまなビジネス上の問題を解決するために使用されます。確率母関数を理解し、適切に使用することで、リスク管理や意思決定プロセスを向上させるのに役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the binomial distribution
p = 0.5
n = 5

# Probability generating function for binomial distribution
def pgf(z):
    return (1 - p + p * z) ** n

z_values = np.linspace(0, 1, 400)
pgf_values = [pgf(z) for z in z_values]

plt.figure(figsize=(10, 6))
plt.plot(z_values, pgf_values, label=f'PGF of Binomial Distribution (n={n}, p={p})')
plt.title('Probability Generating Function (PGF)')
plt.xlabel('z')
plt.ylabel('G(z)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()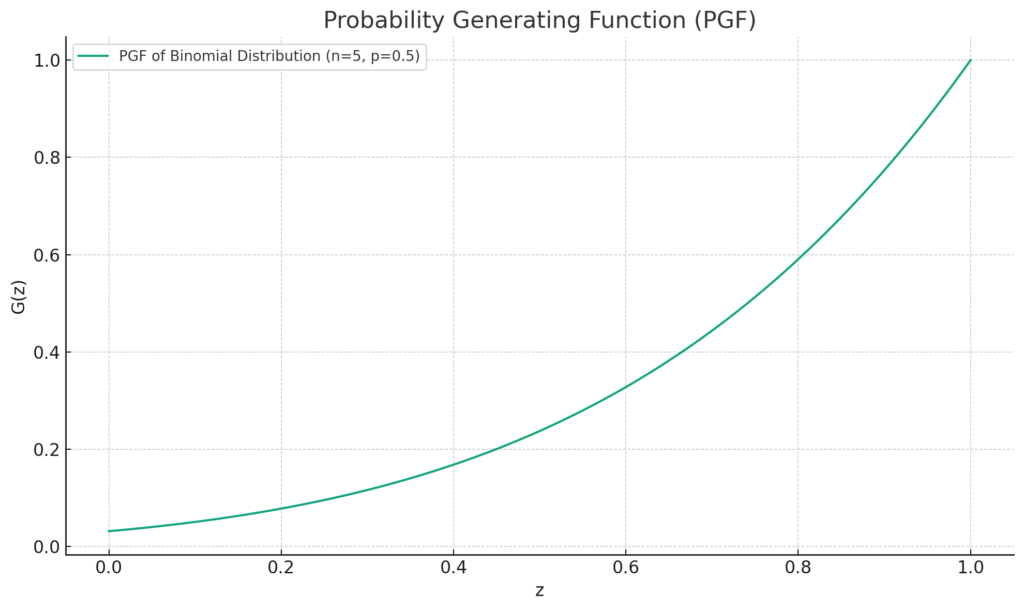

上記のグラフは、試行回数が \( n = 5 \) で成功確率が \( p = 0.5 \) の二項分布の確率母関数（PGF）を示しています。x軸は \( z \) の値（0から1の範囲）を表し、y軸はPGFの値、すなわち \( G(z) \) を表しています。

このグラフから、二項分布における異なる \( z \) の値に対してPGFがどのように振る舞うかを観察できます。PGFは特定のシナリオに基づいてさまざまな離散分布を表現するためにカスタマイズできます。これは、需要の予測、リスクの評価、または金融商品のモデリングであるかに関係なく利用できます。

モーメント母関数

モーメント母関数（Moment Generating Function、略してMGF）は、確率変数の確率分布を特定するための関数です。この関数は、確率変数のモーメント（平均、分散、歪度、尖度など）を生成するために使用されます。モーメント母関数は、確率変数の全てのモーメントを一度に計算するのに便利であり、確率変数の分布を特定するために役立ちます。

モーメント母関数（MGF）は、確率変数のモーメントを計算するための強力なツールです。具体的には、MGFの導関数を評価することで、モーメントを得ることができます。確率変数のモーメント母関数は以下のように定義されます。

\[
M_X(t) = E[e^{tX}]
\]

ここで、\(E[]\) は期待値を示し、\(t\) は任意の実数です。

正規分布のモーメント母関数は以下の式で与えられます。

\[
M_X(t) = e^{\mu t + \frac{1}{2} \sigma^2 t^2}
\]

この場合、\( \mu = 0 \) および \( \sigma^2 = 1 \) です。

ビジネスの応用例

ビジネスや金融の分野で、モーメント母関数は次のような用途で使用されます。

1. リスク評価: 金融データのリターンや価格の確率分布をモデル化するために、モーメント母関数が使用されます。これにより、将来のリスクや変動性を評価し、適切なリスク管理戦略を構築できます。
2. ポートフォリオ最適化: 複数の資産から成る投資ポートフォリオを最適化する際に、各資産の確率分布をモデル化するのにモーメント母関数が役立ちます。これにより、リスクとリターンのトレードオフを詳細に分析できます。
3. 需要予測: 製品の需要の確率分布をモデル化するために、モーメント母関数が使用されます。これにより、需要の確率的な変動を予測し、在庫管理や生産計画を最適化できます。
4. 統計的解析: データセットの統計的性質を調べるために、モーメント母関数が使用されます。データの分布、平均、分散、歪度、尖度などの統計的特性を調査し、意思決定に役立つ洞察を得るのに役立ちます。

モーメント母関数は確率変数の特性を詳細に調査し、ビジネスや金融のさまざまな側面で重要な役割を果たす統計的ツールです。確率変数のモーメント情報を提供し、意思決定やリスク評価に基づいた戦略を構築するのに役立ちます。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the normal distribution
mu = 0
sigma2 = 1

# Moment Generating Function for a normal distribution
def mgf(t):
    return np.exp(mu * t + 0.5 * sigma2 * t**2)

# Values for t
t_values = np.linspace(-2, 2, 400)

# Calculate MGF values
mgf_values = mgf(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_values, label=f'MGF of Normal({mu}, {sigma2})', color='blue')
plt.title('Moment Generating Function of a Normal Distribution')
plt.xlabel('t')
plt.ylabel('M_X(t)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()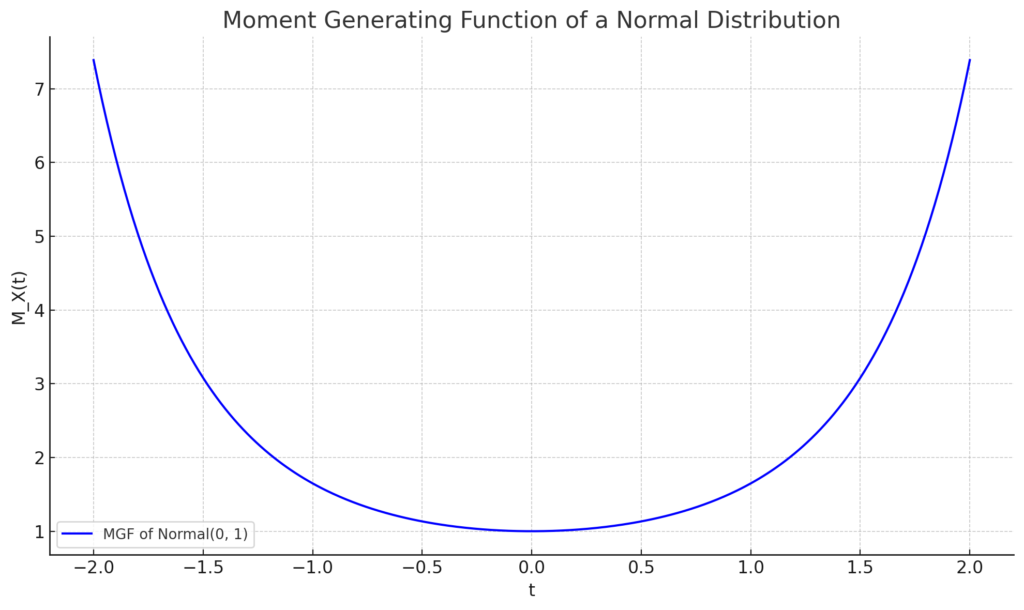

上のグラフは、平均 \( \mu = 0 \)、分散 \( \sigma^2 = 1 \) の正規分布に対するモーメント母関数 \( M_X(t) \) を示しています。x軸は \( t \) の値を、y軸はモーメント母関数の値を示しています。

モーメント母関数を視覚的に描画することで、確率分布の特性や振る舞いを理解するのに役立ちます。特に、モーメント母関数の形状や振る舞いは、対応する確率分布の特性を反映しています。

ビジネスや金融の文脈でのモーメント母関数の利用は、データの特性や振る舞いを深く理解し、より正確な予測や意思決定を行うための基盤となります。

確率母関数とモーメント母関数の関係

確率母関数とモーメント母関数は、確率変数の特性を調べるための数学的なツールであり、確率論や統計学の分野で重要な役割を果たします。

確率母関数は、離散型確率変数の確率分布を表現するための関数です。確率母関数は、確率変数の各値に対する確率を生成します。具体的には、離散確率変数\(X\)の確率質量関数（各値の確率を示す関数）を生成します。確率母関数は、一般的に\(z\)という変数に対する関数として次のように表されます。

\[G(z) = E[z^X]\]

ここで、\(E\)は期待値を表し、\(X\)は確率変数です。確率母関数は、\(z\)に特定の値を代入することで、それに対応する確率を生成します。

モーメント母関数 (Moment Generating Function, MGF):

モーメント母関数は、確率変数の特性を調べるための関数で、確率変数のモーメント（平均、分散、歪度、尖度など）を生成するために使用されます。モーメント母関数は、確率変数\(X\)に対する\(t\)という変数に対する期待値の関数として次のように表されます。

\[M_X(t) = E[e^{tX}]\]

ここで、\(E\)は期待値を表し、\(X\)は確率変数です。モーメント母関数は、\(t\)に特定の値を代入することで、それに対応するモーメントを生成します。例えば、\(t\)を0に代入すると、モーメント母関数は平均の値になります。

ビジネスへの応用:

確率母関数とモーメント母関数は密接に関連しています。実際、確率母関数を十分に微分可能な場合、モーメント母関数は確率母関数を用いて以下のように表されます。

\[M_X(t) = G_X(e^t)\]

この関係により、確率母関数からモーメント母関数を容易に求めることができます。逆に、モーメント母関数を使用することで、確率変数のモーメント（平均、分散など）を直接計算できます。

ビジネスの応用例

ビジネスの応用例としては、需要予測や金融データの分析があります。商品の需要予測では、確率母関数やモーメント母関数を使用して需要の確率分布をモデル化し、在庫管理や生産計画を最適化します。金融データの分析では、リスクの評価やリターンの予測に確率母関数やモーメント母関数が活用され、投資戦略やポートフォリオ最適化に役立てられます。

確率母関数とモーメント母関数は、確率変数の特性を理解し、ビジネスや統計解析において確率分布をモデル化し、意思決定に役立つ情報を提供するための重要な数学的ツールです。

Pythonコード

確率母関数とモーメント母関数の関係を視覚的に示すために、以下の手順でグラフを作成します。

1. 確率母関数 \( G(z) \) を計算します。この例では、簡単のために2点分布を考えます。この分布は確率 \( p \) で 1 の値をとり、確率 \( 1-p \) で 0 の値をとるとします。
2. モーメント母関数 \( M_X(t) \) を計算します。これは、上記の確率母関数を用いて \( M_X(t) = G_X(e^t) \) の関係式を使用して計算します。
3. これらの関数を同じグラフにプロットして、比較を行います。

以下はPythonを使用してこのグラフを描画するコードです。

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the binomial distribution
p = 0.5

# Probability Generating Function (PGF)
def G(z):
    return (1-p) + p*z

# Moment Generating Function (MGF) derived from PGF
def MGF(t):
    return G(np.exp(t))

# Values for plotting
t_values = np.linspace(-2, 2, 400)

# Compute PGF and MGF values
G_values = [G(np.exp(t)) for t in t_values]
MGF_values = [MGF(t) for t in t_values]

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, G_values, label="PGF: $G(e^t)$", color='blue')
plt.plot(t_values, MGF_values, label="MGF: $M_X(t)$", color='red', linestyle='--')
plt.title("Relationship between PGF and MGF")
plt.xlabel("$t$")
plt.ylabel("Function Value")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()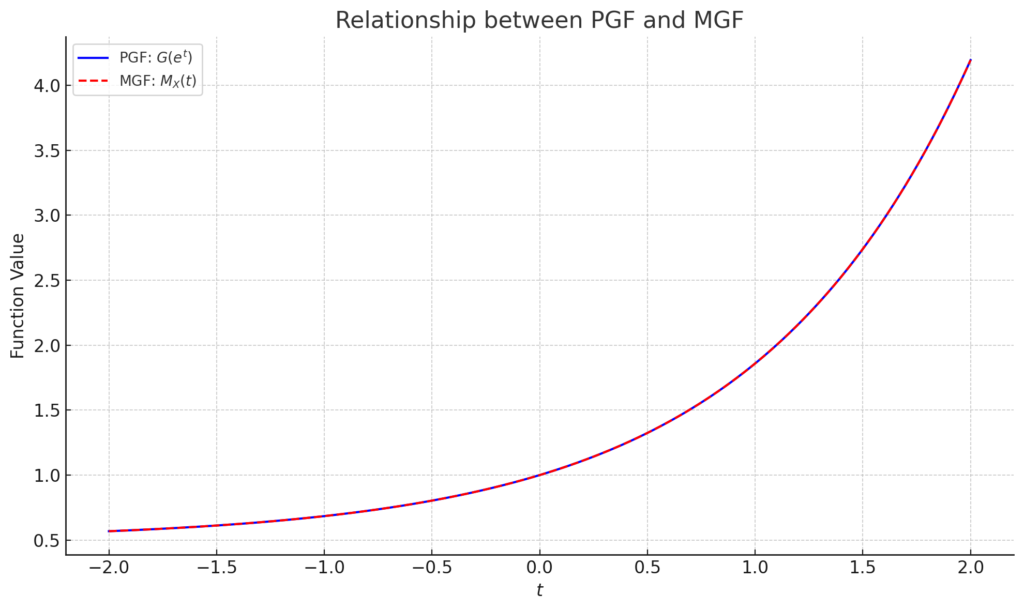

このグラフは、確率母関数 (PGF: \(G(e^t)\)) とモーメント母関数 (MGF: \(M_X(t)\)) の関係を示しています。青色の線は確率母関数を、赤色の破線はモーメント母関数を示しています。

\( t \) の値に対して、両関数の振る舞いを比較できます。この視覚的な比較により、確率母関数とモーメント母関数の違いと関連性を理解するのが容易になります。

ビジネスや統計解析の文脈では、このような視覚的なツールは、データの特性や分布の特徴を迅速に理解し、意思決定をサポートするための洞察を提供するのに役立ちます。

連続的な確率変数のモーメント母関数

連続的な確率変数のモーメント母関数は、その確率変数の特性を調べるための数学的なツールです。この関数は、確率変数の各モーメント（平均、分散、歪度、尖度など）を生成するために使用されます。

連続的な確率変数のモーメント母関数の定義:

連続的な確率変数(X)のモーメント母関数は、(t)という変数に対する期待値の関数として次のように表されます。

ここで、(E)は期待値を表し、(X)は連続的な確率変数です。モーメント母関数は、(t)に特定の値を代入することで、それに対応するモーメントを生成します。例えば、(t)を0に代入すると、モーメント母関数は確率変数(X)の平均値（期待値）になります。

ビジネスの応用例

連続的な確率変数のモーメント母関数は、ビジネスや統計学においてさまざまな応用があります。以下はいくつかの応用例です。

1. 滞在時間の分析: 顧客がある場所に滞在する時間（例: オンラインショッピングサイトの滞在時間）をモデル化および分析するために使用できます。モーメント母関数を通じて、滞在時間の平均や分散を計算し、サイトの改善やマーケティング戦略の最適化に役立ちます。
2. 製品の寿命分析: 製品の寿命（例: 電子機器の寿命）を評価し、信頼性を向上させるために使用できます。モーメント母関数を介して寿命分布の特性を調べ、製品の品質管理に貢献します。
3. リスク評価: 金融分野では、資産価格の確率分布やリスクの評価にモーメント母関数を使用します。これにより、投資戦略の検討やポートフォリオ管理に役立つ情報を得ることができます。
4. 信号処理: 信号処理の分野では、信号の特性やスペクトル解析においてモーメント母関数が使用されます。これにより、通信システムの設計やデジタル信号処理の最適化が行われます。

連続的な確率変数のモーメント母関数は、データの特性を理解し、ビジネスや科学分野での意思決定に役立つ情報を提供するための強力なツールです。特に、確率分布の形状や特性を調べ、データの分析とモデリングに活用されます。

Pythonコード

連続的な確率変数\( X \)のモーメント母関数\( M_X(t) \)は次のように定義されます。

\[
M_X(t) = E[e^{tX}]
\]

標準正規分布の場合、この期待値は次のように計算されます。

\[
M_X(t) = e^{\frac{t^2}{2}}
\]

この式を使用して、モーメント母関数のグラフを作成します。

import numpy as np
import matplotlib.pyplot as plt

# Moment Generating Function for a standard normal distribution
def MGF(t):
    return np.exp(t**2 / 2)

# Values of t for which to compute the MGF
t_values = np.linspace(-2, 2, 400)

# Compute the MGF for each value of t
mgf_values = MGF(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_values, label="MGF of Standard Normal Distribution", color='blue')
plt.title("Moment Generating Function (MGF) of Standard Normal Distribution")
plt.xlabel("t")
plt.ylabel("M_X(t)")
plt.grid(True)
plt.legend()
plt.show()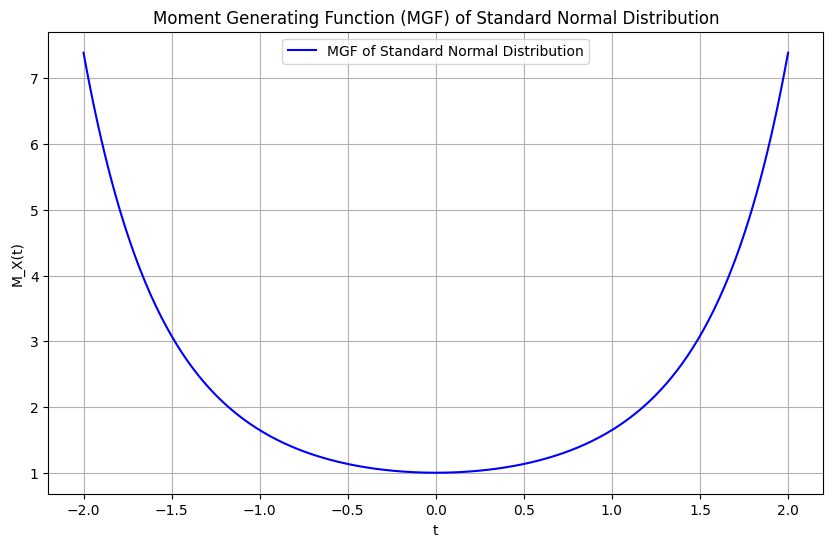

上記のコードを実行すると、標準正規分布のモーメント母関数のグラフが表示されます。このグラフは、モーメント母関数が \( t \) の異なる値に対してどのように振る舞うかを示しています。特に、\( t = 0 \) のとき、モーメント母関数は1になり、これは標準正規分布の平均値（期待値）を示しています。

正規分布のモーメント母関数

正規分布のモーメント母関数は、正規分布の特性を調べるための数学的なツールです。この関数は、正規分布の確率変数のすべてのモーメント（平均、分散、歪度、尖度など）を生成するために使用されます。

正規分布のモーメント母関数の定義:

正規分布のモーメント母関数は、\(t\)という変数に対する期待値の関数として次のように表されます。

\[M_X(t) = E[e^{tX}]\]

ここで、\(E\)は期待値を表し、\(X\)は正規分布に従う確率変数です。モーメント母関数は、\(t\)に特定の値を代入することで、それに対応するモーメント（平均、分散、歪度、尖度など）を生成します。

ビジネスの応用例

正規分布のモーメント母関数は、ビジネスや統計学においてさまざまな応用があります。

1. 売上の予測: 商品の売上データが正規分布に従うと仮定される場合、モーメント母関数を使用して売上の平均値や変動を推定し、将来の売上を予測します。これは在庫管理や生産計画に役立ちます。
2. ウェブサイト分析: ウェブサイトの訪問者数や滞在時間などのデータが正規分布に近い場合、モーメント母関数を使用してウェブサイトの性能を分析し、改善の方針を立てます。
3. 金融リスク評価: 資産価格の変動が正規分布に従うと仮定される場合、モーメント母関数を介してリスク評価を行います。これは投資ポートフォリオの構築やリスク管理に役立ちます。
4. 製造プロセスの品質管理: 製造プロセスからの製品データが正規分布に従う場合、モーメント母関数を使用して製品品質の統計的プロセス管理（SPC）を行います。これにより、不良率の低減や品質向上が可能です。

正規分布は統計学で広く使用され、多くの実世界のデータが正規分布に近いと仮定されるため、正規分布のモーメント母関数はデータの特性を理解し、ビジネス上の意思決定を裏付けるための重要なツールです。

Pythonコード

正規分布のモーメント母関数は、平均 \( \mu \) と標準偏差 \( \sigma \) をパラメータとして持つ正規分布に対して、次のように表されます。

\[
M_X(t) = e^{\mu t + \frac{1}{2} \sigma^2 t^2}
\]

この関数は、正規分布の平均 \( \mu \) と標準偏差 \( \sigma \) との関係を示しています。

以下は、このモーメント母関数をプロットするPythonコードです。この例では、平均 \( \mu = 0 \) と標準偏差 \( \sigma = 1 \) の標準正規分布のモーメント母関数を描画します。

import numpy as np
import matplotlib.pyplot as plt

# Moment Generating Function for a normal distribution
def MGF_normal(t, mu=0, sigma=1):
    return np.exp(mu * t + 0.5 * sigma**2 * t**2)

# Values of t for which to compute the MGF
t_values = np.linspace(-2, 2, 400)

# Compute the MGF for each value of t
mgf_values = MGF_normal(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_values, label="MGF of Normal Distribution", color='blue')
plt.title("Moment Generating Function (MGF) of Normal Distribution")
plt.xlabel("t")
plt.ylabel("M_X(t)")
plt.grid(True)
plt.legend()
plt.show()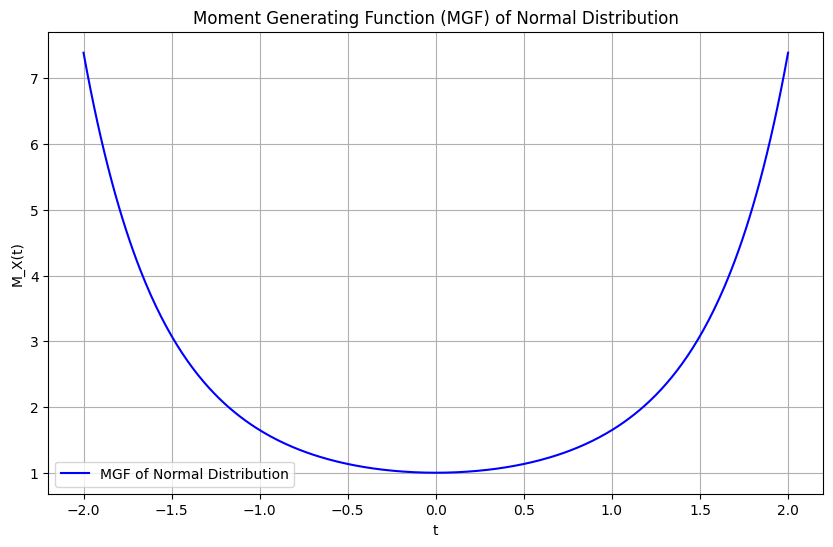

上記のコードを実行すると、標準正規分布のモーメント母関数のグラフが表示されます。このグラフは、モーメント母関数が \( t \) の異なる値に対してどのように振る舞うかを示しています。

X^2分布のモーメント母関数

\(X^2\)分布のモーメント母関数は、\(X^2\)分布の特性を調べるための数学的なツールです。この関数は、\(X^2\)分布の確率変数のすべてのモーメント（平均、分散、歪度、尖度など）を生成するために使用されます。

\(X^2\)分布のモーメント母関数の定義:

\(X^2\)分布のモーメント母関数は、\(t\)という変数に対する期待値の関数として次のように表されます。

\[M_X(t) = E[e^{tX}]\]

ここで、\(E\)は期待値を表し、\(X\)は\(X^2\)分布に従う確率変数です。モーメント母関数は、\(t\)に特定の値を代入することで、それに対応するモーメント（平均、分散、歪度、尖度など）を生成します。

ビジネスの応用例

\(X^2\)分布のモーメント母関数は、ビジネスや統計学においてさまざまな応用があります。以下はいくつかの応用例です。

1. 品質管理: 製品の製造プロセスからのデータが\(X^2\)分布に従う場合、モーメント母関数を使用して品質管理の統計的プロセス管理（SPC）を行います。これにより、製品の品質を維持し、不良率を低減します。
2. 信頼性テスト: 製品や材料の信頼性をテストする際に、\(X^2\)分布を使用することがあります。信頼性テストでは、寿命データや故障データが\(X^2\)分布に従うことが考えられ、モーメント母関数を用いて信頼性の評価を行います。
3. 医学研究: 医学研究において、\(X^2\)分布はさまざまな実験や臨床試験の結果の解析に使用されます。特に、疾患の治療効果やリスク因子の評価に役立ちます。

\(X^2\)分布は統計学やデータ分析において重要な確率分布であり、ビジネスや科学分野での多くの問題に適用できるため、そのモーメント母関数はデータの特性を理解し、意思決定を裏付けるための有用なツールです。

Pythonコード

\(X^2\)分布、またはカイ二乗分布のモーメント母関数は、自由度\( k \)を持つカイ二乗分布に対して次のように表されます。

\[
M_X(t) = (1 – 2t)^{-k/2}
\]

ただし、\( t < \frac{1}{2} \)。

以下は、このモーメント母関数をプロットするPythonコードです。この例では、自由度 \( k = 5 \) のカイ二乗分布のモーメント母関数を描画します。

import numpy as np
import matplotlib.pyplot as plt

# Moment Generating Function for a chi-squared distribution
def MGF_chisquared(t, k=5):
    return (1 - 2*t)**(-k/2)

# Values of t for which to compute the MGF
t_values = np.linspace(-0.49, 0.49, 400)  # t should be less than 0.5

# Compute the MGF for each value of t
mgf_values = MGF_chisquared(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_values, label="MGF of Chi-squared Distribution with k=5", color='blue')
plt.title("Moment Generating Function (MGF) of Chi-squared Distribution")
plt.xlabel("t")
plt.ylabel("M_X(t)")
plt.grid(True)
plt.legend()
plt.show()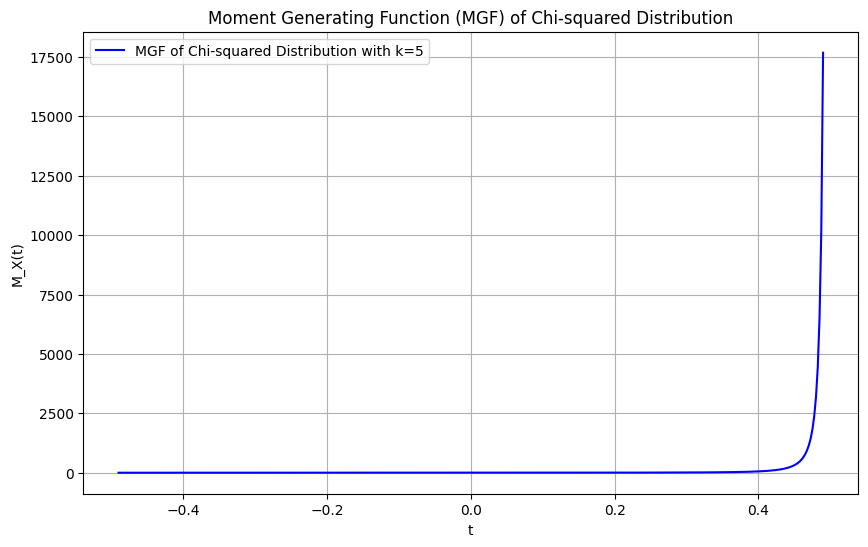

上記のコードを実行すると、自由度 \( k = 5 \) のカイ二乗分布のモーメント母関数のグラフが表示されます。このグラフは、モーメント母関数が \( t \) の異なる値に対してどのように振る舞うかを示しています。

2つの正規分布の平均の差のモーメント関数

2つの正規分布の平均の差のモーメント関数は、2つの異なる正規分布からのデータを比較するための統計的手法に関連しています。この関数は、2つの正規分布からのデータの平均値の差がどのように分布するかを調べるために使用されます。

2つの正規分布の平均の差のモーメント関数の定義:

2つの異なる正規分布からのサンプルデータを考えると、それぞれの正規分布における平均値を\(μ_1\)と\(μ_2\)とし、標本サイズ（サンプルサイズ）を\(n_1\)および\(n_2\)とします。これらのデータから計算される2つの平均値の差を\(X_1\)と\(X_2\)とします。このとき、2つの正規分布の平均の差のモーメント関数は、次のように定義できます。

\[M(t) = E[e^{t(X_1 – X_2)}]\]

ここで、\(E\)は期待値を表し、\(t\)はパラメータです。この関数は、2つの正規分布からのサンプルデータに基づいて、平均の差の分布を特定の\(t\)に対して評価します。これにより、2つの正規分布の平均値の差がどのように分布するかを調べることができます。

ビジネスの応用例

2つの正規分布の平均の差のモーメント関数は、ビジネスや科学分野でさまざまな応用があります。

1. 製品比較: 異なる2つの製品やサービスのパフォーマンスを比較するために使用されます。たとえば、新製品と既存製品の効果を比較して、どちらが優れているかを評価する場合に役立ちます。
2. クリニカルトライアル: 新薬とプラセボの効果を比較する臨床試験で使用されます。2つの治療法の平均効果の差が統計的に有意かどうかを評価するためにこの関数が適用されます。
3. 市場調査: 異なる市場戦略や広告キャンペーンの効果を比較するために使用されます。どの戦略が市場で最も効果的であるかを判断するためのデータ解析に役立ちます。

2つの正規分布の平均の差のモーメント関数は、2つのデータセットを比較し、統計的な差異を評価するための重要な統計手法の一つです。ビジネスや研究において、異なるグループや条件の効果を評価する際に、この関数がデータ解析に役立つことがあります。

Pythonコード

2つの正規分布の平均の差のモーメント母関数の説明を考慮すると、以下のポイントが重要です。

1. \( X_1 \) と \( X_2 \) はそれぞれ独立な正規分布からのサンプルの平均です。
2. \( X_1 \) の分布は \( N(\mu_1, \sigma_1^2/n_1) \) で、\( X_2 \) の分布は \( N(\mu_2, \sigma_2^2/n_2) \) です。
3. \( X_1 – X_2 \) の分布は \( N(\mu_1 – \mu_2, \sigma_1^2/n_1 + \sigma_2^2/n_2) \) です。

これらの情報を使用して、\( X_1 – X_2 \) のモーメント母関数をプロットします。

以下は、このモーメント母関数をプロットするPythonコードです。この例では、以下のパラメータを使用します。

\( \mu_1 = 5 \)
\( \mu_2 = 3 \)
\( \sigma_1^2 = 4 \)
\( \sigma_2^2 = 9 \)
\( n_1 = 100 \)
\( n_2 = 100 \)

import numpy as np
import matplotlib.pyplot as plt

# Parameters
mu1, mu2 = 5, 3
sigma1, sigma2 = np.sqrt(4), np.sqrt(9)
n1, n2 = 100, 100

# Difference distribution parameters
mu_diff = mu1 - mu2
sigma_diff = np.sqrt(sigma1**2/n1 + sigma2**2/n2)

# Moment Generating Function for the difference of two normals
def MGF_diff(t):
    return np.exp(mu_diff * t + 0.5 * (sigma_diff**2) * t**2)

# Values of t for which to compute the MGF
t_values = np.linspace(-2, 2, 400)

# Compute the MGF for each value of t
mgf_values = MGF_diff(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_values, label="MGF of Difference of Two Normals", color='blue')
plt.title("Moment Generating Function (MGF) of Difference of Two Normal Distributions")
plt.xlabel("t")
plt.ylabel("M(t)")
plt.grid(True)
plt.legend()
plt.show()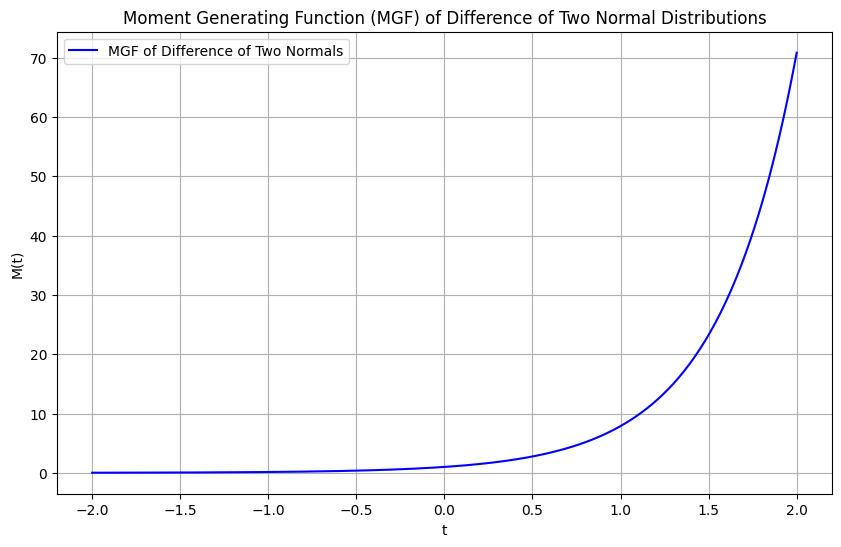

上記のコードを実行すると、2つの正規分布の平均値の差のモーメント母関数のグラフが表示されます。このグラフは、モーメント母関数が \( t \) の異なる値に対してどのように振る舞うかを示しています。

独立的な確率変数の和のモーメント関数 = それぞれのモーメント母関数の積

独立な確率変数の和のモーメント関数は、確率変数が独立している場合に、それぞれの確率変数のモーメント母関数の積として求められます。これは、統計的な問題を解析する際に、複数の確率変数からなるデータの特性を簡単に計算するための有用な道具です。

独立な確率変数の和のモーメント関数の定義:

考えている確率変数が \(X_1, X_2, X_3, \ldots, X_n\) のように複数あり、これらが互いに独立である場合を考えましょう。それぞれの確率変数 \(X_i\) に対するモーメント母関数が \(M_i(t)\) で表されるとします。このとき、これらの確率変数の和 \(S = X_1 + X_2 + X_3 + \ldots + X_n\) のモーメント母関数 \(M_S(t)\) は、以下のように計算されます。

\[M_S(t) = M_1(t) \cdot M_2(t) \cdot M_3(t) \cdot \ldots \cdot M_n(t)\]

つまり、各確率変数のモーメント母関数を掛け合わせることで、和の確率変数 \(S\) のモーメント母関数が得られます。

ビジネスの応用例

この概念はビジネス分野でも幅広く応用されます。例えば、以下のような場面で役立ちます。

1. クリック数の合計: 複数の広告キャンペーンやウェブサイトからのクリック数を合計する際に、それぞれの広告キャンペーンのクリック数の分布を知りたい場合に使用します。各広告キャンペーンのクリック数が独立である場合、合計のクリック数の分布を計算するためにこの概念が役立ちます。
2. 在庫の需要予測: 複数の商品の需要予測を合算する際に、それぞれの商品の需要の確率分布を利用して、合計の需要の確率分布を求めることができます。
3. リスク評価: リスク分析において、異なるリスク要因が独立している場合、それぞれの要因のリスクを組み合わせて全体のリスクを評価するために使用します。

このように、複数の独立な事象や確率変数からなるデータを統合して合計の分布や特性を理解する場合、独立な確率変数の和のモーメント関数の概念がとても役立ちます。

Pythonコード

2つ以上の独立な確率変数の和のモーメント母関数が、それぞれのモーメント母関数の積であるという考え方は、数学的にとても強力です。この考え方を視覚的に示すために、2つの正規分布を考えて、それぞれのモーメント母関数とその和のモーメント母関数をプロットしてみます。

以下の例では、次の2つの正規分布を考えます。

1. \( X_1 \) : 平均 \( \mu_1 = 2 \)、分散 \( \sigma_1^2 = 1 \)
2. \( X_2 \) : 平均 \( \mu_2 = 4 \)、分散 \( \sigma_2^2 = 2.5 \)

各正規分布のモーメント母関数は以下のように表されます。

\[ M_{X_1}(t) = \exp(\mu_1 t + \frac{1}{2} \sigma_1^2 t^2) \]
\[ M_{X_2}(t) = \exp(\mu_2 t + \frac{1}{2} \sigma_2^2 t^2) \]

和のモーメント母関数 \( M_S(t) \) は次のようになります。

\[ M_S(t) = M_{X_1}(t) \times M_{X_2}(t) \]

以下はこの情報を使用して、モーメント母関数をグラフにプロットするPythonコードです。

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the two normal distributions
mu1, sigma1 = 2, 1
mu2, sigma2 = 4, np.sqrt(2.5)

# Moment generating functions for the two normals
def MGF_X1(t):
    return np.exp(mu1 * t + 0.5 * sigma1**2 * t**2)

def MGF_X2(t):
    return np.exp(mu2 * t + 0.5 * sigma2**2 * t**2)

# MGF for the sum of the two normals
def MGF_S(t):
    return MGF_X1(t) * MGF_X2(t)

# Values of t for which to compute the MGF
t_values = np.linspace(-2, 2, 400)

# Compute the MGFs for each value of t
mgf_X1_values = MGF_X1(t_values)
mgf_X2_values = MGF_X2(t_values)
mgf_S_values = MGF_S(t_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(t_values, mgf_X1_values, label="MGF of $X_1$", color='blue')
plt.plot(t_values, mgf_X2_values, label="MGF of $X_2$", color='green')
plt.plot(t_values, mgf_S_values, label="MGF of $S$", color='red', linestyle='--')
plt.title("Moment Generating Functions (MGF)")
plt.xlabel("t")
plt.ylabel("M(t)")
plt.grid(True)
plt.legend()
plt.show()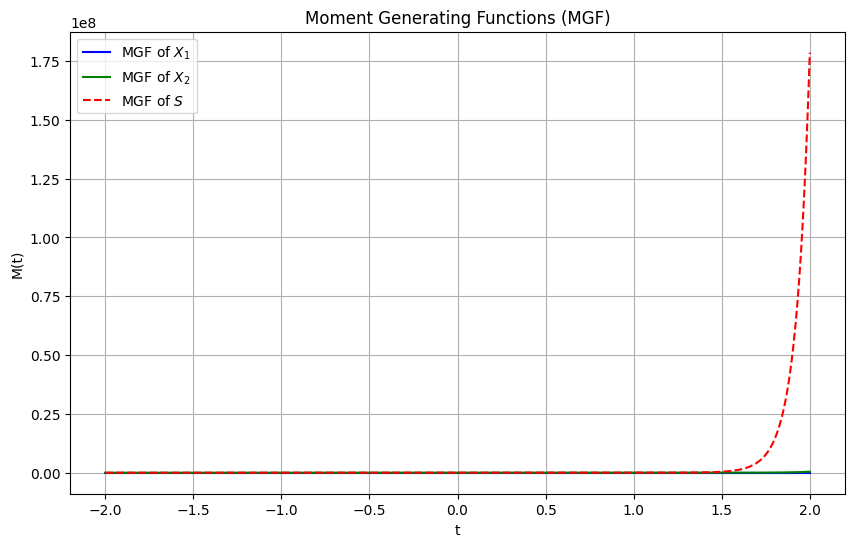

このコードを実行すると、2つの正規分布のモーメント母関数とその和のモーメント母関数のグラフが表示されます。

機械学習

【実践で学ぶ機械学習】《回帰編》広告費からクリック数を予測する

回帰（Regression）は、統計学や機械学習の分野で使用される手法の一つで、連続値を予測するための方法です。回帰の目的は、与えられた入力データから、特定の連続値や数値を予測することです。具体的な例として、広告費からクリック数を予測するケースを考えてみましょう。

1. 広告費とクリック数の関係: ある企業がオンライン広告にお金をかけて広告を表示し、その結果、何人のユーザーがその広告をクリックするかを知りたいとします。広告費とクリック数は関連しており、広告費が増えればクリック数も増える可能性があると考えられます。
2. 回帰分析の適用: この問題を解決するために、回帰分析を適用します。回帰モデルは、過去のデータ（広告費とクリック数のペア）を学習し、そのパターンをもとに新しい広告費の値に対するクリック数を予測します。
3. 回帰モデルの学習: 回帰モデルは、広告費を入力として受け取り、それに基づいてクリック数を予測する関数を学習します。この関数は通常、直線や曲線の形を取ります。直線モデルの場合、式は次のようになります。クリック数 = a * 広告費 + b。ここで、a は直線の傾き（広告費とクリック数の関連性を示す）、b は直線の切片です。
4. 予測の利用: 学習した回帰モデルを使用して、新しい広告費の値を入力すると、モデルはそれに対するクリック数を予測します。この予測は、広告戦略の最適化や予算配分などのビジネス上の意思決定に役立ちます。

回帰は与えられたデータから連続値を予測する方法であり、広告費からクリック数を予測する場合、回帰モデルはその予測を行います。この予測を通じて、企業は広告キャンペーンの効果を評価し、意思決定に役立てることができます。

問題設定（Problem Setting）

問題設定（Problem Setting）は、データ科学や機械学習プロジェクトの最初のステップであり、解決したい問題を明確に定義する段階です。具体的な例として、広告費を元にクリック数を予測する問題を考えてみましょう。

1. 問題の背景: 企業がオンライン広告を実施しており、その広告にかける費用（広告費）に対して、ユーザーが広告をクリックした回数（クリック数）の変動があることが観察されています。企業は、広告費を調整することでクリック数を最大化したいと考えています。
2. 問題の明確化: 問題設定の最初のステップは、この課題を明確に定義することです。つまり、広告費とクリック数の関係を数値的に理解し、広告費が増減するとクリック数がどのように変化するかを明らかにしたいという目標が設定されます。
3. データ収集: 問題を解決するためには、過去の広告費とそれに対応するクリック数のデータを収集する必要があります。これにより、問題に対するデータセットが得られ、分析とモデルの構築に利用できるようになります。
4. モデルの選択: 問題設定では、どの種類のモデルを使用して予測を行うかも検討します。この例では、回帰モデル（広告費からクリック数を予測するためのモデル）が適していると考えられます。
5. 評価指標の設定: 問題設定では、成功を測定するための評価指標も決定されます。例えば、予測されたクリック数と実際のクリック数の誤差を最小化することが目標である場合、平均二乗誤差（Mean Squared Error）などの評価指標が選ばれることがあります。

問題設定はプロジェクトの基盤であり、問題を明確に理解し、その後のステップ（データ収集、モデリング、評価など）を効果的に進めるための重要なステップです。広告費とクリック数の予測問題では、広告戦略の最適化や広告予算の最適化に貢献します。

モデル定義（Model Definition）

モデル定義（Model Definition）は、データ科学や機械学習において、問題を解決するために数学的なモデルを選択するステップです。具体的な例として、広告費とクリック数の関係を予測する問題を考えてみましょう。この例では、線形回帰モデルがモデル定義の一部として選択されます。

1. モデルの役割: モデルは、与えられたデータに基づいて、そのデータの背後にある関係性やパターンを捉えるための数学的な道具です。広告費とクリック数の問題では、広告費が増減するとクリック数にどのような影響を与えるかを理解するためにモデルが必要です。
2. モデルの選択: モデル定義では、どの種類のモデルを使用するかを選択します。この例では、線形回帰モデルが選択されています。線形回帰モデルは、広告費とクリック数の関係を直線的な関係としてモデル化するもので、数式的には y = mx + b のように表されます。ここで、y はクリック数、x は広告費、m は直線の傾き、b は切片を表します。
3. モデルの適合度: モデルはデータに適合させる必要があります。つまり、モデルのパラメータ（傾き m と切片 b）を調整して、実際のデータに最も近似する直線を見つける必要があります。これにより、広告費からクリック数を予測するためのモデルが構築されます。
4. モデルの評価: モデルがデータにどれだけ適合しているかを評価するために、評価指標（例: 平均二乗誤差）を使用します。この評価指標は、モデルの予測が実際のデータとどれだけ近いかを示します。

モデル定義は、問題に適したモデルを選択し、そのモデルをデータに適合させるプロセスです。この例では、線形回帰モデルが広告費とクリック数の関係を表現するために使用され、広告戦略や予算の最適化に役立ちます。

最小二乗法（Least Squares）

最小二乗法（Least Squares）は、線形回帰モデルのパラメータ（傾きと切片）を推定するための統計的手法です。この手法は、データと線形モデルによる予測の誤差を最小化することを目指します。以下のステップで最小二乗法が動作します。

1. データの収集: まず、実際のデータが収集されます。例えば、広告費とクリック数の関係を理解したい場合、異なる広告費に対応するクリック数のデータが必要です。
2. モデルの定義: 線形回帰モデルを選択し、数式的には y = mx + b のように表します。ここで、y はクリック数、x は広告費、m は傾き、b は切片を表します。
3. 予測値の計算: モデルを使って、与えられた広告費に対してクリック数を予測します。つまり、モデルを使って y を計算します。
4. 誤差の計算: 実際のデータと予測値との差、つまり誤差を計算します。誤差は、各データポイントにおける実際の値と予測値の差を示します。
5. 誤差の二乗の合計を最小化: 最小二乗法の目標は、誤差の二乗（誤差を正の値に変換し、大きな誤差をよりペナルティを受けるようにするため）の合計を最小化するパラメータ m（傾き）と b（切片）を見つけることです。これにより、実際のデータに最も適合する直線が得られます。
6. 最適な予測直線の取得: 最小二乗法によって見つけられた最適なパラメータ m と b に基づいて、最適な予測直線を得ることができます。この直線は、広告費とクリック数の関係性を最もよく表現するものです。

最小二乗法は、データに基づいて線形モデルのパラメータを調整し、実際のデータに最も適合する予測モデルを得るための一般的な手法です。線形回帰モデルの場合、この方法によって広告費からクリック数を予測するための最適な直線を見つけることができます。

最急降下法（Gradient Descent）

最急降下法（Gradient Descent）は、機械学習や最適化のアルゴリズムでよく使用される手法で、目的関数を最小化するために使われます。最小二乗法のように、モデルのパラメータを調整し、目的関数を最小化するための一般的なアプローチです。以下に、最急降下法の基本的な考え方を説明します。

1. 目的関数（コスト関数）の定義: 最急降下法では、最小化したい目的関数（通常、予測誤差の合計など）を定義します。この目的関数は、モデルのパラメータに依存し、そのパラメータを調整することで最小化されるべきものです。
2. 初期パラメータの設定: 最急降下法のスタート地点となる初期パラメータを設定します。通常、ランダムな値やゼロに初期化されます。
3. 勾配の計算: 目的関数の勾配（変化率）を計算します。勾配は、目的関数が最も急速に減少する方向を示します。具体的には、各パラメータに対して偏微分を行い、その値を使って勾配ベクトルを作成します。
4. パラメータの更新: 勾配ベクトルを使って、各パラメータを更新します。これは、目的関数を最小化する方向にパラメータを移動させるステップです。具体的な更新式は以下のようになります。

   新しいパラメータ = 古いパラメータ - (学習率) * (勾配)

ここで、学習率はステップの大きさを制御するハイパーパラメータです。学習率が大きすぎると発散し、小さすぎると収束が遅くなる可能性があります。

5. 収束の確認: パラメータの更新を繰り返し行い、目的関数が収束するまで続けます。収束は、目的関数の変化が小さくなり、最適なパラメータが見つかったことを示します。

最急降下法は、目的関数を最小化するための効率的な方法であり、機械学習モデルの訓練に広く使用されます。特に、線形回帰やニューラルネットワークなどのモデルのパラメータ調整に適しています。

多項式回帰（Polynomial Regression）

多項式回帰（Polynomial Regression）は、線形回帰の一種で、データの関係性を直線ではなく曲線（多項式）で表現するための手法です。線形回帰が直線的な関係性を仮定するのに対し、多項式回帰は曲線的な関係性を捉えることができます。これにより、データの実際のパターンにより適合したモデルを構築できます。

1. 曲線的な関係性のモデル化: 多項式回帰は、データが直線的な関係性では説明できない場合に役立ちます。例えば、広告費とクリック数の関係が曲線的で、広告費が増えるとクリック数が指数関数的に増加する場合などです。
2. 多項式の次数: 多項式回帰では、関係性を表現するために多項式の次数を選択します。次数は多項式の項の数を決定し、高次の多項式はより複雑な曲線を表現できます。しかし、高次の多項式を使用すると、過学習のリスクが高まることがあるため、注意が必要です。
3. モデルの方程式: 多項式回帰のモデルは通常以下のような方程式で表現されます。

   y = β₀ + β₁x + β₂x² + ... + βₖxᵏ + ε

ここで、yは目的変数（予測対象の値）、xは説明変数（広告費など）、kは選択した多項式の次数、β₀, β₁, β₂, …, βₖは回帰係数、εは誤差を表します。

4. 適切な次数の選択: 多項式回帰を適切に使用するためには、適切な次数を選択することが重要です。次数が低すぎるとデータのパターンを捉えきれず、次数が高すぎると過学習のリスクがあるため、交差検証などの手法を用いて適切な次数を見つける必要があります。

多項式回帰は、実際のデータに適用する際に、関係性が複雑な場合や単純な直線モデルでは不十分な場合にとても役立つ手法です。データの特性に基づいて最適な次数を選択し、より柔軟なモデルを構築できます。

重回帰（Multiple Regression）

重回帰（Multiple Regression）は、回帰分析の一種で、複数の説明変数（特徴量）を使用して目的変数（予測対象の値）を予測するための手法です。単回帰とは異なり、1つの説明変数だけでなく、複数の説明変数を組み合わせて目的変数を予測します。これにより、複数の要因が予測対象に影響を与える場合に、より現実的な予測モデルを構築できます。

以下に、重回帰のポイントを説明します。

1. 複数の説明変数: 重回帰では、1つ以上の説明変数を利用します。これらの説明変数は、予測対象に影響を与える要因や特徴を表します。例えば、広告のクリック数を予測する場合、広告費、広告の表示位置、曜日、時間帯、競合他社の広告などが説明変数として考えられます。
2. モデルの方程式: 重回帰のモデルは通常以下のような方程式で表現されます。

   y = β₀ + β₁x₁ + β₂x₂ + ... + βₖxₖ + ε

ここで、yは目的変数、x₁, x₂, …, xₖは説明変数、β₀, β₁, β₂, …, βₖは回帰係数、εは誤差を示します。各説明変数の回帰係数は、それぞれの変数が予測対象に与える影響を示します。

3. 多重共線性の考慮: 複数の説明変数を使用する場合、これらの変数間に相関が高い場合、多重共線性と呼ばれる問題が発生することがあります。多重共線性はモデルの解釈性を損なう可能性があるため、注意が必要です。
4. モデルの解釈: 重回帰モデルを解釈する際には、各説明変数の回帰係数の意味を理解することが重要です。回帰係数が正であれば、その説明変数が増加すると目的変数も増加することを示し、負であれば逆の関係を示します。
5. モデルの評価: 重回帰モデルの評価には、回帰係数の統計的有意性、決定係数（モデルの適合度）、残差分析などが含まれます。これらの評価を通じて、モデルの妥当性を確認します。

重回帰は、実世界の問題において複数の要因が影響を与える場合に有用な手法です。例えば、商品の売上予測、住宅価格の予測、健康指標の予測など、多くのビジネスや科学分野で広く利用されています。

確率的勾配降下法（Stochastic Gradient Descent, SGD）

確率的勾配降下法（Stochastic Gradient Descent、SGD）は、機械学習と深層学習における最適化アルゴリズムの一つで、モデルのパラメータを訓練データに適合させるための方法です。SGDは、大規模なデータセットやリアルタイム学習の場面で特に有用です。以下、SGDの主要な特徴と動作について説明します。

1. 最急降下法の一種: SGDは、最急降下法（Gradient Descent）の一種です。最急降下法は、目的関数（損失関数）を最小化するために、関数の勾配（変化率）を利用してパラメータを更新します。SGDも同様に、目的関数の最小化を目指しますが、データの一部（ランダムに選ばれたサンプル）を使用して計算を効率化します。
2. ランダムなサンプリング: SGDは、訓練データ全体ではなく、ランダムに選ばれた1つまたは複数のサンプルを使用して勾配を計算します。このランダムなサンプリングが「確率的」な要素です。これにより、データセットがとても大きい場合でも、計算コストを削減できます。
3. イテレーション: SGDは、訓練データ全体を複数回繰り返し学習します。各イテレーション（反復）で、ランダムに選ばれたサンプルを使用してモデルのパラメータを更新します。このプロセスは、データ全体に対する複数のイテレーションを通じて続けられます。
4. 学習率: SGDには学習率と呼ばれるハイパーパラメータがあります。学習率は、各イテレーションでパラメータをどれだけ更新するかを制御します。適切な学習率を選択することが、SGDの収束性と性能に影響を与えます。
5. 確率的性質: SGDは確率的な性質を持つため、ノイズの影響を受けます。このため、収束までに多少の振れが生じることがありますが、大規模なデータセットに対しても高速に収束する利点があります。

SGDは、特に深層学習モデルのトレーニングに広く使用されており、大規模なニューラルネットワークの訓練を可能にします。また、リアルタイムでデータが増え続ける状況（オンライン学習）や、メモリが制限された環境でも役立ちます。しかし、適切な学習率や収束のコントロールが必要であるため、ハイパーパラメータの調整が重要です。

【実践で学ぶ機械学習】《分類編》画像サイズに基づいて分類する

分類（Classification）

分類（Classification）は、機械学習やデータ分析の中で、入力データを特定のカテゴリやクラスに分けるタスクを指します。具体的には、与えられたデータポイントが、事前に定義されたいくつかのカテゴリの中でどれに属するかを予測する作業です。

例えば、「画像サイズに基づいて分類する」というタスクを考えてみましょう。この場合、与えられた画像データを異なるクラス（例: 犬、猫、車、飛行機など）に分類することが目的となります。分類モデルは、画像の特徴を解析し、それがどのクラスに最も類似しているかを判断します。

分類の主要なポイント:

1. カテゴリまたはクラス: 分類では、データを分ける対象となるカテゴリやクラスが事前に定義されています。各データポイントは、これらのクラスの中から1つに割り当てられます。
2. トレーニングデータ: 分類モデルを訓練するために、トレーニングデータセットが使用されます。トレーニングデータには、各データポイントが正しいクラスに所属するラベルが付いています。
3. 特徴抽出: モデルは、データの特徴を分析してクラスを予測します。画像の場合、ピクセルの明るさや色、テキストの場合、単語の出現頻度など、適切な特徴が選択されます。
4. モデルの訓練: モデルは、トレーニングデータを使用して特徴とクラスの関係を学習します。学習プロセスでは、モデルのパラメータが調整され、正確な予測が行えるようになります。
5. テストデータ: 訓練が完了したモデルは、新しいデータポイントまたはテストデータに適用されます。モデルは各データポイントを分類し、予測されたクラスを出力します。
6. 評価: テストデータの予測結果は、真のラベルと比較され、モデルの性能が評価されます。一般的な評価メトリクスには、正解率、適合率、再現率、F1スコアなどがあります。

分類は幅広い応用分野で利用されており、例えばスパムメールの検出、手書き文字認識、疾患の診断、画像認識、自然言語処理など、さまざまなタスクで重要です。分類モデルの設計とトレーニングは、正確な予測を行いたい多くの実務上の問題に対する鍵となる要素です。

問題設定（Problem Setting）

問題設定（Problem Setting）は、機械学習やデータ分析プロジェクトにおいて、解決したい具体的な問題をはっきりと定義し、プロジェクトの方針を設定するステップです。

1. 問題の明確な定義: 最初に、何を解決しようとしているのか、どのような課題に取り組むのかを明確に定義します。このステップでは、具体的な目標や成果物を明示化します。例えば、スパムメールを検出する、画像を分類する、売上を予測するなど、問題が何であるかを確認します。
2. データの収集と整理: 問題を解決するためには、関連するデータが必要です。この段階で、どのようなデータが必要であり、それらをどのように収集・整理するかを計画します。データの品質、利用可能なデータソース、データのフォーマットなどを考慮します。
3. 問題の種類: 問題設定には、主に次の3つの種類があります。

• 分類問題（Classification）: データポイントを複数のクラスまたはカテゴリに分ける問題。例えば、スパムメールの分類。
• 回帰問題（Regression）: 連続値を予測する問題。例えば、不動産価格の予測。
• クラスタリング問題（Clustering）: データを類似性に基づいてグループ分けする問題。例えば、顧客セグメンテーション。

1. 評価基準: 問題を解決するために、どのように成功を評価するかを明確に定義します。評価基準は、問題の種類によって異なります。分類問題であれば正解率、回帰問題であれば平均二乗誤差などが一般的です。
2. ビジネスのコンテキスト: 問題設定には、ビジネスや実務上の文脈も考慮されます。問題解決がどのようにビジネスに貢献するか、どのような意義があるかを理解し、ビジネス目標との整合性を確保します。
3. プロジェクトの進行計画: 問題設定に基づいて、プロジェクトの進行計画を策定します。データ収集、モデルの選定、トレーニング、評価、展開などのステップを明確に計画し、プロジェクト全体の方向性を示します。

問題設定の適切な実施は、プロジェクトが正しい方向に進み、問題解決が成功するために不可欠なステップです。クリアな問題の定義は、データ収集、モデル選択、評価、ビジネス価値の実現において基盤となります。

内積（Dot Product）

内積（Dot Product）は、2つのベクトル（ベクトルは数値の並びです）の間で行われる演算の一つで、ベクトルの各要素同士を掛け合わせて合計する操作です。内積は、ベクトル同士の類似性や関連性を評価するのに役立ちます。

具体的には、2つのベクトルを考えてみましょう。ベクトルAとベクトルBが以下のように定義されているとします。

ベクトルA = [a1, a2, a3, …, an]
ベクトルB = [b1, b2, b3, …, bn]

このとき、ベクトルAとベクトルBの内積（Dot Product）は次のように計算されます。

内積(A・B) = (a1 * b1) + (a2 * b2) + (a3 * b3) + … + (an * bn)

内積は各要素同士を掛け合わせ、その結果を合計した値です。内積の計算を通じて、2つのベクトルがどれだけ似ているか、またはどれだけ関連性があるかを評価できます。

内積の応用例:

1. ベクトルの類似性評価: 自然言語処理や情報検索などで、文章や文書をベクトル化して、それらのベクトル間の類似性を計算するのに内積が使用されます。類似した文章を見つけたり、関連性の高い文書を検索したりするのに役立ちます。
2. 機械学習モデルの特徴量重要度: 機械学習モデルでは、各特徴量の重要度を評価するために内積が使用されることがあります。特徴量とターゲット変数との関連性を測定し、モデルの学習や特徴選択に活用されます。

内積は数学的な基本演算であり、ベクトル解析や線形代数など多くの分野で重要な役割を果たします。

パーセプトロン（Perceptron）

パーセプトロン（Perceptron）は、とてもシンプルな機械学習モデルの一つで、入力データを分類するために使用されます。パーセプトロンは線形分類器の一種であり、以下の方法で動作します。

1. 入力ベクトルと重みベクトルの内積計算: パーセプトロンは、入力データを表すベクトルと対応する重みベクトルの内積（ドット積）を計算します。この内積は、各入力要素とその重みの積を合計することで得られます。数式で表すと、次のようになります。 内積 = (入力ベクトル)・(重みベクトル) この内積の計算により、入力データが特定の重み付き組み合わせで表現されます。
2. 閾値の適用: パーセプトロンは、計算された内積に対して、ある閾値（しきい値）を適用します。内積が閾値を超える場合と超えない場合で、2つの異なるクラスに分類されます。

• 内積 ≥ 閾値: クラス1に分類
• 内積 < 閾値: クラス2に分類

このように、パーセプトロンは入力データを2つのクラスに分類するための線形モデルです。入力ベクトルと重みベクトルの内積が閾値を超えるかどうかで、クラス分類が行われます。

パーセプトロンの特徴と応用:

• パーセプトロンは線形分類器であるため、線形に分離可能な問題に対して適しています。
• 複数のパーセプトロンを組み合わせることで、より複雑な非線形分類を実現することも可能です（多層パーセプトロン、ニューラルネットワーク）。
• パーセプトロンは古典的な機械学習アルゴリズムであり、基本的な理解を深めるための学習ツールとしても利用されます。

ただし、パーセプトロンは限定的な問題にしか適用できず、線形分離不可能なデータには適していません。そのため、より高度なモデルやニューラルネットワークが線形分離不可能な問題に対処するために使用されます。

データの準備（Data Preparation）

データの準備（Data Preparation）は、機械学習モデルを訓練し、評価する前に、データを整える重要な工程です。データの品質と整合性を確保するために行われます。以下は、データの準備に含まれる主要なタスクです。

1. データ収集: まず、必要なデータを収集します。これは、問題に対処するために必要な情報を含むデータセットやデータソースを取得するプロセスです。
2. データのクリーニング: 収集したデータを検査し、不正確な、不完全な、または不要なデータをクリーンアップします。これには、欠損値（空白やNaN値）、外れ値（異常な値）、重複データの処理などが含まれます。
3. 特徴量エンジニアリング: データの特徴量（説明変数）を適切に設計します。これは、モデルの性能に大きな影響を与える要素で、特徴量の選択、スケーリング、変換、新しい特徴量の生成などが含まれます。
4. データの分割: データを訓練用とテスト用に分割します。通常、データの大部分を訓練に使用し、一部をモデルの評価に予約します。このステップにより、モデルの一般化性能を評価できます。
5. データの正規化: データを特定の尺度や範囲に合わせて正規化します。これは、異なる特徴量の値の範囲が異なる場合に、モデルの学習を助けるために行われます。例えば、特徴量の値を0から1の範囲にスケーリングすることがあります。
6. カテゴリカルデータのエンコーディング: カテゴリカルデータ（文字列やカテゴリ）を数値データに変換する必要がある場合、エンコーディング手法を使用します。例えば、ワンホットエンコーディングは、カテゴリカル変数を0と1のバイナリ変数に変換します。
7. データのバッチ化: 大規模なデータセットを小さなバッチに分割して、モデルの学習を効率的に行うために使用します。特に深層学習モデルでは、バッチ学習が一般的です。
8. データの確認と可視化: データの特性や分布を確認し、可視化して理解することが重要です。異常値や傾向を検出し、モデルの学習における決定を補完するために使用します。

データの準備は、モデルの性能に直接影響を与えるため、慎重かつ注意深く行う必要があります。データが整えられたら、モデルの学習と評価に進むことができます。

重みベクトルの更新式（Updating Weights）

重みベクトルの更新式は、機械学習アルゴリズムで使用されるパラメータである「重み」を調整するための数式です。特に、分類タスクにおいて、モデルが誤った予測を行った場合、重みを修正して正しい予測に近づけるのに使われます。以下に重みベクトルの更新式の概要を示します。

1. 分類タスクと誤差: 重みベクトルの更新は、分類タスクでの予測の誤差に基づいて行われます。分類誤差は、モデルがデータポイントを誤って分類した場合に生じる差異を表します。
2. 目的関数（損失関数）: 通常、重みベクトルの更新は、ある目的関数（または損失関数）の最小化を目指します。この目的関数は、モデルの予測と実際の正解との間の誤差を評価するもので、誤差が小さいほど目的関数の値が小さくなります。
3. 最急降下法: 最も一般的な重みベクトルの更新方法は、最急降下法（Gradient Descent）です。最急降下法では、目的関数の勾配（傾き）を計算し、その逆方向に重みを微小なステップで更新します。これにより、目的関数を最小化する方向に重みが移動し、モデルの性能が向上します。
4. 学習率: 重みベクトルの更新時には、学習率と呼ばれるハイパーパラメータを導入します。学習率は、重みの調整幅を制御します。大きすぎる学習率は収束を妨げ、小さすぎる学習率は収束までに時間がかかる可能性があります。適切な学習率を選ぶことが重要です。
5. 重みの更新式: 一般的な重みの更新式は以下のように表されます。 新しい重み = 旧い重み – 学習率 × 勾配 この式では、学習率を掛けた勾配を旧い重みから引いて新しい重みを計算します。勾配は目的関数の微分であり、目的関数が最小値に向かう方向を示します。
6. 反復的な更新: 重みの更新は通常、訓練データセットの各データポイントに対して反復的に行われます。訓練データを順次処理しながら重みを更新し、目的関数を最小化します。

重みベクトルの更新式は、モデルがデータに適合し、正しい予測を行うための重要な要素です。最急降下法をはじめとする更新アルゴリズムを適切に設定し、目的関数を最小化するように重みを調整することで、モデルの性能を向上させることができます。

線形分離可能（Linearly Separable）

線形分離可能（Linearly Separable）とは、データが直線または超平面と呼ばれる平坦な面で、2つの異なるクラスに完全に分割できる場合の状況を指します。これは、特に機械学習アルゴリズムでの分類タスクに関連しています。

1. データの性質: データが線形分離可能である場合、それはデータポイント（例: サンプル、観測値）が2つの異なるクラス（カテゴリ）に属し、それらのクラスを完全に分けるための直線または平面が存在することを意味します。つまり、クラスAに属するデータポイントはこの直線の一方の側にあり、クラスBに属するデータポイントは他方の側にあります。
2. パーセプトロンと学習: パーセプトロンは、線形分離可能なデータセットに対しては、正しく分類できることが理論的に保証されています。パーセプトロンは線形決定境界を学習し、この境界を使用してデータポイントをクラスに分類します。
3. 例: 線形分離可能な例として、2つのクラスを持つ簡単なデータセットを考えてみましょう。例えば、赤と青の点が混在する平面上で、赤い点を1つのクラスとし、青い点を別のクラスとする場合、これらの点を完全に分ける直線が存在します。
4. 限界: ただし、現実の多くの問題では、データが完全に線形分離可能であることは稀です。実際のデータはノイズや重なりが含まれ、完全な分離が難しい場合があります。そのため、機械学習では非線形モデルや複雑なモデルも使用され、より複雑なデータセットに適合できるようになっています。

線形分離可能な場合、パーセプトロンのような線形分類器はとても効果的ですが、問題ではデータが複雑であることが一般的です。そのため、非線形な分類器や、データの前処理や特徴量エンジニアリングなどの手法が必要な場合があります。

ロジスティック回帰（Logistic Regression）

ロジスティック回帰（Logistic Regression）は、線形回帰を基にした機械学習の分類手法です。線形回帰が連続値を予測するのに対して、ロジスティック回帰は2つのクラス（通常は「0」と「1」または「陰性」と「陽性」など）の分類を行います。

1. 線形回帰の限界: 線形回帰は、入力特徴量（説明変数）と連続値の目的変数（予測したい値）の関係を直線でモデル化する手法です。しかし、クラス分類の問題では、目的変数が2つのクラスに分かれている場合が一般的であり、直線だけでは適切に分類できないことがあります。
2. シグモイド関数: ロジスティック回帰は、線形回帰の出力をシグモイド関数（またはロジスティック関数）と呼ばれる特別な関数に通すことで、確率的な出力を得ます。シグモイド関数はS字型の曲線で、0から1の値を取ります。これにより、線形回帰の出力を0から1の範囲に変換し、確率として解釈できるようにします。
3. 確率の解釈: ロジスティック回帰の出力は、あるデータが所属するクラスの確率を表します。例えば、0.7の確率で「陽性」クラスに属するという出力は、そのデータが「陽性」に分類される確率が70%であることを示します。
4. 決定境界: ロジスティック回帰のモデルは、シグモイド関数によって変換された確率を基に、あるデータを1つのクラスまたはもう一つのクラスに分類します。分類のための境界は、シグモイド関数の出力が通常0.5である点です。この点を境界として、確率が0.5以上なら1つのクラスに、0.5未満ならもう一つのクラスに分類されます。
5. 学習とパラメータ調整: ロジスティック回帰の目標は、与えられたデータセットに最適なシグモイド関数のパラメータ（重みとバイアス）を見つけることです。これは、最尤推定法や勾配降下法を用いて行われます。

ロジスティック回帰は、二項分類（2つのクラスに分ける問題）にとても有用であり、多くの機械学習アプリケーションで広く使用されています。

シグモイド関数（Sigmoid Function）

シグモイド関数（Sigmoid Function）は、実数を0から1の間の値に変換する特別な数学関数です。この関数はS字型の曲線を描き、主にロジスティック回帰やニューラルネットワークなどで使用され、確率を表現するのに役立ちます。

1. S字型の曲線: シグモイド関数は、その名前が示すように”S”の字を逆さまにしたような形をしています。この曲線は、入力値に対して急速に変化し、0から1までの値を取ります。具体的な数式で表すと、次のようになります。 $$\sigma(z) = \frac{1}{1 + e^{-z}}$$ ここで、$\sigma(z)$はシグモイド関数を表し、$z$は入力値です。
2. 確率の変換: シグモイド関数は、その出力を0から1の範囲に変換するため、確率を表現するのに適しています。特に、0から1までの範囲の値は、ある出来事が発生する確率を表すのに使われます。例えば、0.7のシグモイド関数の出力は、その出来事が発生する確率が70%であることを示します。
3. ロジスティック回帰: シグモイド関数は、ロジスティック回帰などの分類アルゴリズムで使用されます。ロジスティック回帰では、入力データの特徴量と重みを組み合わせて計算された値をシグモイド関数に入力し、その出力をもとに2つのクラス（通常は0と1）にデータを分類します。シグモイド関数によって、この出力が確率として解釈され、例えば0.5以上なら1のクラスに、0.5未満なら0のクラスに分類されると決まります。
4. ニューロンの活性化関数: シグモイド関数は、ニューラルネットワークの活性化関数としても使用されます。ニューラルネットワークは、入力信号の重み付けと活性化関数によって情報を伝え、シグモイド関数はこの活性化関数の一つとして、ニューロンの出力を0から1の範囲に変換します。

シグモイド関数は入力を確率的な値に変換する役割を果たし、分類やニューラルネットワークなどで広く使用されています。そのS字型の曲線は、確率を表現するのに適しています。

決定境界（Decision Boundary）

決定境界（Decision Boundary）は、分類問題において2つの異なるクラスを分けるための境界線や境界面のことを指します。

1. 分類問題の境界線: 決定境界は、機械学習や統計の分類問題において、2つの異なるクラス（例えば、0と1、陰性と陽性、青い点と赤い点など）を分けるための境界線や境界面を表します。この境界は、データポイントがどのクラスに属するかを決定する基準となります。
2. ロジスティック回帰の例: ロジスティック回帰では、シグモイド関数によって計算された出力が0.5以上の場合に1のクラスに分類し、0.5未満の場合に0のクラスに分類します。このとき、シグモイド関数の出力が0.5のときの境界線が決定境界となります。つまり、決定境界は、クラス分類のしきい値を示すもので、それを境にデータが異なるクラスに分類されます。
3. 図示化: 決定境界は、通常、データの特徴空間において、クラスが交わる場所や変化する地点を示す線、曲線、または超平面として図示されます。例えば、2次元の場合では直線または曲線となり、3次元以上の場合では超平面となります。
4. モデルの性能評価: 決定境界は、分類モデルの性能を評価する際にも重要です。モデルがどのようにデータを分離するかによって、モデルの性能が判断されます。適切な決定境界は、正確なクラス分類を実現するために重要です。

決定境界は、分類問題において異なるクラスを分けるためのラインや面のことであり、モデルのクラス分類を決定する基準として機能します。ロジスティック回帰の例では、シグモイド関数の出力がこの決定境界の位置を決定します。

尤度関数（Likelihood Function）

尤度関数（Likelihood Function）は、統計学や機械学習において、あるモデルの現在のパラメータ設定のもとで、観測データが得られる確率を数学的に表現する関数です。尤度関数は以下のポイントで説明できます。

1. パラメータの評価: 尤度関数は、特定のモデルがデータをどれだけうまく説明できるかを評価するために使用されます。モデルのパラメータを調整し、観測データが最も高い確率で生成されるようにすることが目標です。
2. 尤度と確率の違い: 尤度関数は観測データが得られる確率を表現しますが、確率密度関数や確率質量関数とは異なります。尤度はデータが得られる条件付き確率の関数で、観測データは既に与えられているものと考えます。つまり、尤度は「既に観測されたデータがこのモデルでどれだけ起こりやすかったか」を評価します。
3. 最尤推定: 尤度関数を用いて、最尤推定（Maximum Likelihood Estimation, MLE）と呼ばれる手法を実行します。最尤推定は、尤度を最大化するようにモデルのパラメータを調整する方法で、データに適合するベストなパラメータ設定を見つけるのに役立ちます。
4. 通常の確率分布との関係: 尤度関数は、通常の確率分布の形式とは異なります。通常の確率分布では、特定の事象が起こる確率を示すのに対し、尤度関数は既に起こった事象を説明する確率を示します。

尤度関数はあるモデルとそのパラメータ設定が観測データをどれだけ説明できるかを評価するための数学的なツールです。最尤推定を通じて、モデルのパラメータを調整し、データに最も適合するモデルを見つけるのに利用されます。

対数尤度関数（Log-Likelihood Function）

対数尤度関数（Log-Likelihood Function）は、尤度関数の対数を取った関数です。尤度関数自体は、あるモデルのパラメータ設定が観測データをどれだけ説明できるかを示すものであり、対数尤度関数はこの尤度関数を対数変換したものです。

1. 尤度関数の対数変換: 対数尤度関数は尤度関数を対数（通常は自然対数）を取って計算されます。これにより、尤度関数の掛け算（積）が対数尤度関数では足し算（和）に変換され、計算が簡単になります。
2. 最大化の利点: 対数尤度関数は、尤度関数を最大化するという問題を、対数変換によって対数尤度関数を最小化する問題に変換します。最小化問題は、最適化アルゴリズムを使用して容易に解くことができます。そのため、パラメータの最適化に対数尤度関数がよく使用されます。
3. 数値安定性: 多くの場合、対数尤度関数を使用することで数値的な安定性が向上します。特に小さな確率や尤度の値を扱う場合、対数変換は数値的なアンダーフローやオーバーフローを避けるのに役立ちます。
4. 統計的推定: モデルのパラメータを統計的に推定する場合、最尤推定（Maximum Likelihood Estimation, MLE）に対数尤度関数が使われます。最尤推定は、対数尤度関数を最小化するパラメータを見つけることで、データに適合するベストなモデルを見つける方法です。

対数尤度関数は尤度関数を数値的に扱いやすくし、最適化アルゴリズムを使用してモデルのパラメータを最適化する際に役立つものです。特に統計モデリングや機械学習において、対数尤度関数は一般的なツールとして利用されています。

尤度関数の微分（Gradient of Likelihood Function）

尤度関数の微分（Gradient of Likelihood Function）は、統計モデルのパラメータを調整するために使用される数学的なツールです。具体的には、尤度関数を最大化または最小化するために、その関数が最速で増加または減少する方向を示します。以下は尤度関数の微分の要点です。

1. 尤度関数の目的: 尤度関数は、ある統計モデルのパラメータ設定が観測データをどれだけよく説明できるかを示します。尤度関数の目的は、この関数を最大化または最小化することによって、モデルのパラメータを最適化することです。
2. 微分と勾配: 尤度関数の微分は、尤度関数の各パラメータに対する変化率を示すものであり、これを勾配と呼びます。勾配はベクトルで表現され、各パラメータに対する微分値が要素として含まれます。この勾配を使って、最適なパラメータを見つけるための最適化手法（例: 最急降下法、確率的勾配降下法）が適用されます。
3. 最適化: 尤度関数を最大化する場合、勾配を使ってパラメータを増加させる方向を見つけ、最適なパラメータに近づけます。最小化する場合も同様に、勾配を使ってパラメータを減少させる方向を見つけます。このプロセスを反復的に繰り返すことで、最適なパラメータを見つけます。
4. 数値的な計算: 尤度関数の微分は、通常、数値的な計算によって求められます。特に高次元のモデルや複雑な尤度関数の場合、微分を解析的に求めることが難しいため、数値的な近似や計算手法が使用されます。

尤度関数の微分は、モデルのパラメータをデータに最適に適合させるための方向を示し、最適化アルゴリズムを通じてパラメータの調整が行われます。これにより、統計モデルが観測データに最適に適合するようにパラメータが調整され、モデルの性能が向上します。

線形分離不可能（Linearly Inseparable）

線形分離不可能（Linearly Inseparable）とは、データが直線や超平面（平面）で完全に2つのクラスに分けることが難しい、あるいは不可能な場合を指します。これを理解するために、簡単な例を考えてみましょう。

仮想的なデータを考えてみましょう。データが2つのクラス、例えば「円形の点」のクラスと「四角の点」のクラスに分けられる場合を考えます。この場合、円形の点は円の内部にあり、四角の点は円の外部にあるとします。

もし、これらのデータを直線（1次元）や平面（2次元）で分けようとすると、どうしても完璧に分けることはできません。なぜなら、円形の点と四角の点が混在している領域が存在し、どの直線や平面を引いても、必ず両方の点が混ざることになります。

このような場合、データを線形で完全に分けることはできないため、「線形分離不可能」と言います。つまり、直線や平面のような単純な線形モデルでは、これらのデータを適切に分類することは難しいです。

線形分離不可能なデータに対処するためには、非線形モデルや複雑な分類アルゴリズムを使用することが一般的です。例えば、カーネル法を使用したサポートベクトルマシン（SVM）や、深層学習のニューラルネットワークなどが線形分離不可能なデータに対して有効なアプローチです。これらのアルゴリズムは、より複雑な境界を学習し、異なるクラスのデータを効果的に分類できることがあります。

【実践で学ぶ機械学習】《モデル評価編》

モデル評価（Model Evaluation）は、機械学習モデルが実際のデータにどれくらい適合しているかを評価するプロセスです。このプロセスでは、モデルの性能を数値的に評価し、その性能を理解するためのさまざまな指標やメトリクスが使用されます。

モデル評価は、機械学習モデルの性能を評価するための手法です。これは、モデルがデータをどれくらい正確に予測できるかを知るためのプロセスです。評価の際には、いくつかの指標やメトリクスを使用して、モデルの性能を数値化します。これにより、モデルの優れた点や改善が必要な点を特定できます。

ビジネスの応用例：
例えば、金融機関がローン審査の自動化モデルを開発する場合、モデルが正確にリスクの高い顧客を識別できるかを評価する必要があります。正確な予測が重要な場面では、モデル評価は特に重要です。

Pythonコード：
以下のPythonコードは、モデル評価の一例です。このコードは、機械学習モデル（ここではロジスティック回帰モデル）の予測結果と実際のデータ（y_test）を比較して、正解率（accuracy）を計算しています。正解率は、モデルが正しく予測したデータの割合を示す指標で、高いほどモデルの性能が良いことを示します。

from sklearn.metrics import accuracy_score
# モデルを予測する
y_pred = log_reg.predict(X_test_scaled)
# 正解率を計算する
accuracy = accuracy_score(y_test, y_pred)

このコードを使って、モデルの性能を正確性の観点から評価できます。

交差検証:

交差検証（Cross-Validation）は、機械学習モデルの性能を客観的に評価するための手法で、データセットを複数のサブセットに分割し、モデルの性能を複数回評価する方法です。これにより、モデルが未知のデータに対してどれくらいうまく汎化できるかを推定します。

交差検証は、モデルの性能評価に用いられる手法で、モデルの一般化性能を評価するために重要です。通常、データセットはトレーニングデータとテストデータに分割され、モデルはトレーニングデータで学習し、テストデータで性能を評価します。しかし、この方法だけではデータの分割方法に依存してしまい、偶然の要因に影響される可能性があります。

交差検証では、データセットを複数の「フォールド」または「サブセット」に分割し、モデルの性能評価を複数回行います。具体的な手法としては、k分割交差検証（k-fold cross-validation）がよく使われます。この手法では、データセットをk個の同じサイズのフォールドに分割し、k回の評価を行います。各回では、1つのフォールドをテストデータとし、残りのk-1個のフォールドをトレーニングデータとしてモデルを学習・評価します。

Pythonコード：
以下のPythonコードは、scikit-learnライブラリを使用してk分割交差検証を実行する例です。cross_val_score関数は、指定されたモデル（log_reg）、トレーニングデータ（X_train_scaledとy_train）、および分割数（cv=5で5分割）を指定して、各分割におけるモデルの性能を評価し、スコアのリストを返します。これらのスコアの平均値（average_score）を計算することで、モデルの性能を総合的に評価できます。

from sklearn.model_selection import cross_val_score
import numpy as np
# 5分割交差検証を実行
scores = cross_val_score(log_reg, X_train_scaled, y_train, cv=5)
# スコアの平均値を計算
average_score = np.mean(scores)

このコードを使用することで、モデルの性能をより信頼性のある方法で評価できます。

回帰問題の検証:

回帰問題の検証は、機械学習モデルが連続値を予測する能力を評価するプロセスです。回帰モデルは、入力データから実数値の目標値（連続値）を予測するために使用されます。この予測が実際の目標値とどれくらい一致しているかを評価するために、いくつかの指標が使用されます。

1. 平均二乗誤差（Mean Squared Error, MSE）：
平均二乗誤差は、回帰モデルの性能を評価するための一般的な指標の一つです。MSEは、モデルが予測した値と実際の目標値の差を2乗し、それらの平均を計算します。MSEが小さいほど、モデルの予測が実際のデータにより適合していることを示します。計算式は以下の通りです。

\[MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2\]

ここで、\(n\)はデータポイントの数、\(y_i\)は実際の目標値、\(\hat{y}_i\)はモデルによる予測値です。

2. 平均絶対誤差（Mean Absolute Error, MAE）：
平均絶対誤差は、MSEと同様に回帰モデルの性能を評価するための指標ですが、誤差を2乗せずにその絶対値を用います。MAEは、予測値と実際の目標値の差の絶対値の平均です。MSEとは異なり、外れ値（大きな誤差を持つデータポイント）に対して敏感ではありません。計算式は以下の通りです。

\[MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i|\]

Pythonコード：
以下のPythonコードは、scikit-learnライブラリを使用してMSEを計算する例です。まず、モデルによる予測値（y_pred）と実際の目標値（y_test）が用意されています。その後、mean_squared_error関数を使用してMSEを計算します。

from sklearn.metrics import mean_squared_error
# モデルによる予測値の取得
y_pred = regression_model.predict(X_test_scaled)
# 平均二乗誤差（MSE）の計算
mse = mean_squared_error(y_test, y_pred)

このコードを使用することで、回帰モデルの性能をMSEを通じて評価できます。MSEが小さいほど、モデルの性能が良いと言えます。

分離問題の検証:

分離問題の検証は、分類問題で使用されるモデルの性能を評価するプロセスです。分離問題では、データポイントを2つ以上の異なるクラスに分類するタスクがあります。このタスクを実行するモデルの性能を評価するために、いくつかの指標が使用されます。

1. 正解率（Accuracy）：
正解率は、モデルが正しく分類したデータポイントの割合を示す指標です。正解率は以下のように計算されます。

\[正解率 = \frac{正しく分類されたデータポイントの数}{全データポイントの数}\]

正解率が高いほど、モデルの性能が良いと言えます。ただし、クラスの不均衡などの状況では正解率だけでは評価が不十分な場合もあります。

2. F1スコア：
F1スコアは、モデルの精度（Precision）と再現率（Recall）のバランスを示す指標です。F1スコアは以下のように計算されます。

\[F1スコア = \frac{2 \cdot \text{精度} \cdot \text{再現率}}{\text{精度} + \text{再現率}}\]

F1スコアは、精度と再現率のトレードオフを考慮するため、クラスの不均衡な状況でも有用です。F1スコアが高いほど、モデルがバランスの取れた分類を行っていることを示します。

3. 分類レポート（Classification Report）：
分類レポートは、複数の評価指標を一度に表示するための便利な方法です。通常、クラスごとに精度、再現率、F1スコアなどが表示され、さらに全体の平均値も示されます。分類レポートを生成するには、scikit-learnライブラリのclassification_report関数を使用します。以下はその使用例です。

from sklearn.metrics import classification_report
# 分類モデルによる予測結果と実際のクラスラベルを使用して分類レポートを生成
report = classification_report(y_test, y_pred)

この分類レポートを通じて、各クラスにおけるモデルの性能が詳細に分析できます。精度、再現率、F1スコアなどの指標を確認することで、モデルがどのクラスでどれだけ良い予測を行っているかを理解できます。

適合率と再現率

適合率と再現率は、分類モデルの性能を評価するための2つの重要な指標で、特に不均衡なデータセットでの性能評価に役立ちます。

1. 適合率（Precision）：
適合率は、モデルが正と予測したデータのうち、実際に正であったデータの割合を示す指標です。適合率は、偽陽性（実際は負だが、モデルが正と予測した場合）の削減に焦点を当てます。高い適合率は、モデルが正と予測したものが実際に正である確率が高いことを示します。

適合率は以下のように計算されます。

\[適合率 = \frac{\text{真陽性（正と予測し、実際に正）}}{\text{真陽性 + 偽陽性}}\]

2. 再現率（Recall）：
再現率は、実際に正であるデータのうち、モデルが正と予測したデータの割合を示す指標です。再現率は、偽陰性（実際は正だが、モデルが負と予測した場合）の削減に焦点を当てます。高い再現率は、モデルが実際の正のデータを見逃す可能性が低いことを示します。

再現率は以下のように計算されます。

\[再現率 = \frac{\text{真陽性（正と予測し、実際に正）}}{\text{真陽性 + 偽陰性}}\]

Pythonコード：
上記の説明に基づいて、scikit-learnライブラリを使用して適合率と再現率を計算するPythonコードの例を紹介します。モデルによる予測結果（y_pred）と実際のクラスラベル（y_test）を使用します。

from sklearn.metrics import precision_score, recall_score
# 適合率（Precision）の計算
precision = precision_score(y_test, y_pred)
# 再現率（Recall）の計算
recall = recall_score(y_test, y_pred)

このコードを使用することで、モデルの適合率と再現率を計算できます。適合率と再現率のバランスは、特定のタスクやデータセットにおいて最適なモデルの評価基準を提供します。

正則化:

正則化は、機械学習モデルの過学習（過剰適合）を防ぐための技術です。過学習は、モデルが訓練データに対して過度に適合し、新しいデータに対する汎化性能が低下する現象です。正則化は、モデルの複雑さに対してペナルティを課すことで、モデルを簡素化し、汎化性能を向上させます。主にL1正則化とL2正則化の2つの主要なタイプがあります。

1. L1正則化（Lasso正則化）：
L1正則化は、モデルの重み（係数）がゼロに近づくように制約をかけます。つまり、重要でない特徴を無視するように促します。これは特徴選択（不要な特徴の削除）のために役立ちます。L1正則化にはL1ノルム（絶対値の合計）を使用し、正則化項は次のように表されます。

\[L1正則化項 = \alpha \sum_{i=1}^{n} |w_i|\]

ここで、\(w_i\)はモデルの重み（係数）で、\(\alpha\)は正則化の強度を制御するハイパーパラメータです。

2. L2正則化（Ridge正則化）：
L2正則化は、モデルの重みが小さくなるように制約をかけますが、ゼロになることはありません。重みの値が均等になる傾向があります。これはモデルの複雑性を抑え、過学習を防ぐのに役立ちます。L2正則化にはL2ノルム（各要素の二乗の合計）を使用し、正則化項は次のように表されます。

\[L2正則化項 = \alpha \sum_{i=1}^{n} w_i^2\]

同様に、\(\alpha\)は正則化の強度を制御するハイパーパラメータです。

Pythonコード：
上記の説明に基づいて、scikit-learnライブラリを使用してL2正則化（Ridge正則化）を適用するPythonコードの例を紹介します。コードではRidge回帰モデルを作成し、正則化の強度を制御するパラメータ（alpha）を指定しています。

from sklearn.linear_model import Ridge
# Ridge回帰モデルの作成
ridge = Ridge(alpha=1.0)  # alphaは正則化の強度を制御するパラメータ
# モデルの訓練
ridge.fit(X_train_scaled, y_train)

このようにして、正則化を用いたモデルを訓練できます。正則化はモデルの性能を向上させ、過学習を防ぐのに役立ちます。

過学習:

過学習は、モデルが訓練データに過度に適合してしまい、新しいデータに対する予測性能が低下する現象です。

# 過学習を示すコードは特定ではないが、訓練データとテストデータの精度の比較で確認できる
train_score = ridge.score(X_train_scaled, y_train)
test_score = ridge.score(X_test_scaled, y_test)

正規化の方法:

過学習（Overfitting）は、機械学習モデルが訓練データに対して適合しすぎ、新しいデータに対する予測性能が低下する現象です。これは、モデルが訓練データ内の細かなノイズやばらつきまで学習してしまい、訓練データに対してはとても高い性能を示す一方で、新しいデータやテストデータに対してはうまく汎化できない状態を指します。

特徴：

1. 訓練データへの適合度が高い： 過学習のモデルは、訓練データに対してとても高い精度を示します。訓練データ内の個々のデータポイントに対してほぼ完璧な予測ができることがあります。
2. テストデータでの性能が低い： しかし、訓練データ以外の新しいデータ、特にテストデータに対して性能が低いことが過学習の兆候です。モデルが未知のデータにうまく適合できないことがあります。
3. モデルが複雑： 過学習の傾向があるモデルは、通常、とても複雑なモデルです。モデルの自由度が高いため、訓練データの細かなパターンに合わせようとします。

対処方法：

1. データの増加： より多くの訓練データを収集することは、過学習を軽減する一つの方法です。データが増えると、モデルはより一般的なトレンドを学び、細かなノイズに対しては敏感になりにくくなります。
2. モデルの単純化： モデルの複雑性を減らすために、モデルのパラメータ数を制限することが考えられます。例えば、正則化を使用してモデルのパラメータに制約をかけることができます。
3. 交差検証： 交差検証を使用して、モデルの性能を評価し、過学習を検出できます。訓練データとテストデータに対する性能が大きく異なる場合、過学習が発生している可能性があります。
4. 特徴選択： 不要な特徴を削除することにより、モデルの複雑性を減少させます。これにより、モデルがノイズに適合しにくくなります。
5. アンサンブル学習： 複数のモデルを組み合わせて予測を行うアンサンブル学習は、過学習を軽減するのに役立つことがあります。

過学習は機械学習モデルの訓練と評価においてとても重要な問題であり、適切なモデルの選択と調整が必要です。

正則化の効果

正則化は、機械学習モデルの過学習を防ぎ、訓練データに対する適合度とテストデータに対する予測性能のバランスを調整するための強力なツールです。

1. 過学習の制御： 正則化は、モデルが訓練データに対して過度に適合することを制御します。過学習は、モデルが訓練データのノイズや偶発的なパターンに過度に敏感になる現象であり、新しいデータに対しては一般化できなくなります。正則化は、モデルの複雑性を制限し、過学習を軽減します。

2. モデルの一般化： 正則化により、モデルはより一般的なトレンドやパターンを捉えるようになります。これは、訓練データだけでなく、新しいデータに対しても良好な予測性能をもたらします。モデルが適切に一般化されることで、問題に対する適用価値が高まります。

3. パラメータの制御： 正則化は、モデルのパラメータに対してペナルティを課すことで、パラメータの値を制御します。これにより、過度に大きなパラメータ値が抑制され、モデルが過学習しにくくなります。

4. パラメータの選択： 正則化には、L1正則化（ラッソ）とL2正則化（リッジ）の2つの主要なタイプがあり、それぞれ異なる効果があります。L1正則化は特定の特徴を選択し、不要な特徴を削除するのに役立ちます。一方、L2正則化はパラメータの値を小さく保つことに重点を置き、モデル全体の複雑性を減少させます。選択した正則化のタイプによって、モデルの特性を調整できます。

5. ハイパーパラメータ調整： 正則化には強度を調整するハイパーパラメータ（通常、alphaまたはlambdaと呼ばれる）があります。このハイパーパラメータを適切に調整することで、モデルの正則化の強度をコントロールできます。過学習が疑われる場合、alphaまたはlambdaを増加させ、正則化の強度を高めることができます。

正則化は、機械学習モデルの訓練と評価においてとても役立つツールであり、過学習を防ぎ、一般化性能を向上させるのに貢献します。適切な正則化の選択とハイパーパラメータの調整が、モデルの性能を最適化する際に重要です。

学習曲線

学習曲線は、機械学習モデルの性能を評価するためのグラフで、訓練データと検証データのサイズに対するモデルの性能を可視化します。

1. 学習曲線の概要： 学習曲線は、モデルがどの程度訓練データに適合するか、またその性能がデータセットのサイズにどのように依存するかを示すグラフです。通常、横軸に訓練データのサイズ（または学習データの割合）、縦軸に性能指標（例：精度、平均二乗誤差など）がプロットされます。

2. 訓練データと検証データ： 学習曲線は、訓練データと検証データの2つのデータセットに対して性能を示します。訓練データはモデルの訓練に使用され、検証データはモデルの性能評価に使用されます。

3. サイズの変化： 学習曲線では、訓練データのサイズを変化させます。これにより、訓練データのサイズが変化するにつれてモデルの性能がどのように変化するかを観察できます。通常、サイズは横軸にプロットされ、サイズを変化させることで学習曲線を描画します。

4. 学習曲線のパターン： 学習曲線は、次のような一般的なパターンを示すことがあります。

• 過学習（Overfitting）： 訓練データに対する性能が高いが、検証データに対する性能が低い場合。訓練データに過度に適合しており、一般化性能が低いことを示します。
• 未学習（Underfitting）： 訓練データと検証データの両方で性能が低い場合。モデルが訓練データに適合していないことを示し、より複雑なモデルが必要かもしれないことを示唆します。
• 適切な適合： 訓練データと検証データの両方で性能が高く、過学習や未学習の兆候が見られない場合。モデルが適切に一般化されています。

5. Pythonコード： 下記のPythonコードは、scikit-learnライブラリを使用して学習曲線を生成する例です。learning_curve関数を使用して、モデル（この場合はRidge回帰）の性能を訓練データのサイズに対してプロットします。これにより、モデルがどのようにデータのサイズに依存するかを可視化できます。

from sklearn.model_selection import learning_curve
train_sizes, train_scores, valid_scores = learning_curve(
    Ridge(alpha=1.0), X, y, train_sizes=[0.1, 0.33, 0.55, 0.78, 1.], cv=5)

学習曲線を分析することで、過学習や未学習の問題を識別し、モデルの適切な調整や改善の方針を見つけるのに役立ちます。

未学習

未学習（Underfitting）は、機械学習モデルが訓練データに対して不十分な適合度を示す現象です。これは、モデルが過度に単純であるか、または訓練プロセスが不適切である場合に発生します。

特徴：

1. 低い訓練精度： 未学習のモデルは、訓練データに対する予測性能が低い傾向があります。つまり、訓練データ自体に対してもう少し適合する余地があるはずです。
2. 低いテスト精度： 未学習のモデルは、新しいデータ（テストデータなど）に対しても同様に低い予測性能を示します。これは、モデルが一般的なパターンを捉えておらず、新しいデータに適応できていないことを示します。
3. 誤差の高さ： 未学習のモデルは、実際のデータとの誤差が大きい場合があります。つまり、モデルがデータの変動性や複雑さを適切にモデル化できていません。

状況の示唆：

未学習は次のような状況で示唆されることがあります。

• モデルが単純すぎる： モデルがとても単純で、データの複雑な関係性を捉えるのに十分な表現能力がない場合、未学習が発生します。
• 訓練データが不足している： 十分な訓練データが提供されていない場合、モデルはデータの多様性やパターンを学びきれず、未学習の傾向が高まります。
• 適切な特徴量の選択が行われていない： データから適切な特徴量を選択せず、モデルに提供しなかった場合、未学習が発生する可能性があります。

未学習の状態では、モデルが訓練データや新しいデータに対して適切な予測を行えないため、モデルの複雑性を増やす、より適切な特徴量を提供する、またはデータの量を増やすなどの対策が必要です。適切なバランスを見つけるために、モデルの調整と評価が重要です。

過学習と未学習の判別:

過学習（Overfitting）と未学習（Underfitting）を判別するために、訓練データと検証データの性能の差を観察します。

1. 過学習（Overfitting）：

• 特徴： 過学習は、訓練データに対する性能がとても高いが、検証データ（またはテストデータ）に対する性能が低い状態です。つまり、モデルは訓練データに過剰に適合しており、新しいデータに対する一般化がうまくいかないことを示します。
• 状況の示唆： 訓練データにモデルが適合しすぎている場合、複雑なモデルや多くの特徴量を使用した結果、過学習が発生します。モデルは訓練データのノイズや個別の例にまで適合しようとし、そのため一般的なパターンを見逃すことがあります。

2. 未学習（Underfitting）：

• 特徴： 未学習は、訓練データに対する性能が低い状態であり、検証データに対する性能も低いことを示します。つまり、モデルは訓練データに対しても新しいデータに対しても適切な予測を行えていないことを示します。
• 状況の示唆： 未学習は、モデルが単純すぎる、特徴量が不適切、または訓練データが不足している場合に発生します。モデルがデータのパターンを十分に捉えていないため、どちらのデータセットに対しても性能が低いのです。

判別の手法：
過学習と未学習を判別するために、以下の手法を使用できます。

• 性能の比較： 訓練データと検証データ（またはテストデータ）の性能を比較します。訓練データに対する性能がとても高く、検証データに対する性能が低い場合、過学習の兆候があります。
• しきい値の設定： 適切なしきい値（threshold）を設定し、訓練データの性能が検証データの性能よりも大幅に高い場合、過学習と判断できます。

以下のコード例では、しきい値を使用して過学習と未学習を判別する方法が示されています。しきい値を調整して、適切なモデルの状態を判別できます。

if train_score > test_score + threshold:
    print("過学習")
elif train_score < desired_accuracy and test_score < desired_accuracy:
    print("未学習")
else:
    print("適切に学習されている")

訓練データと検証データの性能を比較し、しきい値を設定することで、モデルの過学習や未学習を判別できます。

ディープラーニング

ディープラーニングと画像認識

ディープラーニング（Deep Learning）:
ディープラーニングは、多層のニューラルネットワークを使用してデータを学習する機械学習の手法です。このアプローチでは、入力データを受け取り、多くの中間層（隠れ層）を経て最終的な出力を生成します。各層は、データから特徴を抽出し、次の層に渡します。ディープラーニングの主な利点は、複雑なデータパターンを捉える能力であり、とても高度なタスクを実行できることです。

画像認識:
画像認識は、コンピュータが画像内のオブジェクト、特徴、またはパターンを識別するプロセスです。ディープラーニングは、画像認識においてとても成功しています。具体的には、ディープラーニングモデルは、画像内の物体や特徴を自動的に検出し、認識できます。これにより、自動車の自動運転、医療画像の診断、セキュリティ監視など、さまざまな分野に応用が可能です。

ビジネスの応用例

製造業における品質検査は、ディープラーニングと画像認識の優れたビジネス応用例の一つです。具体的には、以下のようなシステムを構築できます。

• 不良品の自動検出: 製造ライン上で製品の画像を撮影し、ディープラーニングモデルを使用して不良品を自動的に検出します。例えば、製品に傷や欠陥がある場合、その情報をすぐに検出し、品質管理のプロセスに組み込むことができます。

Pythonコード

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
model = Sequential([
    Conv2D(32, (3, 3), activation='relu', input_shape=(150, 150, 3)),
    MaxPooling2D(2, 2),
    Conv2D(64, (3, 3), activation='relu'),
    MaxPooling2D(2, 2),
    Flatten(),
    Dense(512, activation='relu'),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv2d (Conv2D)             (None, 148, 148, 32)      896       
                                                                 
 max_pooling2d (MaxPooling2  (None, 74, 74, 32)        0         
 D)                                                              
                                                                 
 conv2d_1 (Conv2D)           (None, 72, 72, 64)        18496     
                                                                 
 max_pooling2d_1 (MaxPoolin  (None, 36, 36, 64)        0         
 g2D)                                                            
                                                                 
 flatten (Flatten)           (None, 82944)             0         
                                                                 
 dense (Dense)               (None, 512)               42467840  
                                                                 
 dense_1 (Dense)             (None, 1)                 513       
                                                                 
=================================================================
Total params: 42487745 (162.08 MB)
Trainable params: 42487745 (162.08 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

上記のPythonコードは、TensorFlowを使用してディープラーニングモデルを構築する例です。このモデルは、畳み込みニューラルネットワーク（Convolutional Neural Network, CNN）と呼ばれるアーキテクチャを使用しています。CNNは、画像認識タスクに特に適しており、畳み込み層とプーリング層を持つことで画像内の特徴を抽出します。さらに、全結合層（Dense）を使用して最終的な出力を生成します。

このコードは、画像データを入力とし、訓練（学習）プロセスを行います。最終的なモデルは、訓練データから学習されたパラメータを使用して新しい画像を分類できます。

このようなディープラーニングモデルを使えば、製造業などの分野で高度な画像認識タスクを実行するのに役立ちます。

ディープラーニングと自然言語処理

ディープラーニング（Deep Learning）:
ディープラーニングは、多層のニューラルネットワークを使用してデータを学習する機械学習の手法です。これにより、複雑なデータパターンを捉え、高度なタスクを実行できるようになります。

自然言語処理（NLP）:
自然言語処理は、人間が使用する自然言語（テキストや音声）をコンピュータが理解し、処理するための技術です。NLPは、テキストデータを分析し、情報抽出、感情分析、機械翻訳、テキスト分類などのタスクを実行するのに役立ちます。

ビジネスの応用例

ディープラーニングは、自然言語処理の領域でも優れた性能を発揮します。

• カスタマーサポートのチャットボット: ビジネスで最も一般的なNLPの応用例の一つは、カスタマーサポートのチャットボットです。ユーザーからの質問や要求をテキストとして受け取り、ディープラーニングモデルを使用して適切な応答を生成します。これにより、カスタマーサポートの自動化と迅速な対応が可能になります。

Pythonコード

from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Embedding, LSTM, Dense
tokenizer = Tokenizer(num_words=10000, oov_token="<OOV>")
sentences = ["これはテキスト1です。", "これはテキスト2です。", "これはテキスト3です。"]
tokenizer.fit_on_texts(sentences)
sequences = tokenizer.texts_to_sequences(sentences)
padded = pad_sequences(sequences, maxlen=100, truncating='post', padding='post')
model = Sequential([
    Embedding(10000, 64, input_length=100),
    LSTM(64),
    Dense(24, activation='relu'),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.summary()

Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (None, 100, 64)           640000    
                                                                 
 lstm (LSTM)                 (None, 64)                33024     
                                                                 
 dense_2 (Dense)             (None, 24)                1560      
                                                                 
 dense_3 (Dense)             (None, 1)                 25        
                                                                 
=================================================================
Total params: 674609 (2.57 MB)
Trainable params: 674609 (2.57 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

上記のPythonコードは、NLPタスクの一つであるテキスト分類（文をカテゴリに分類する）のためのディープラーニングモデルを構築する例です。

• Tokenizerの使用: Tokenizerは、テキストデータをトークン（単語や句読点などの要素）に分割し、数値データに変換するためのツールです。num_wordsパラメータは、最も頻繁に出現する単語の数を指定します。
• Embedding層: テキストデータを数値ベクトルに変換するために使用されるEmbedding層です。この層は、テキスト内の単語を密なベクトル表現に変換し、モデルの入力として使用します。
• LSTM層: 長短期記憶（Long Short-Term Memory, LSTM）は、シーケンスデータ（テキストなど）を処理するためのリカレントニューラルネットワークの一種です。この層は、テキスト内の文脈を捉えるために使用されます。
• Dense層: ニューラルネットワークの全結合層で、分類タスクにおける最終的な出力を生成します。最終的な分類結果が二値（バイナリ）の場合、sigmoid活性化関数を使用します。

このようなモデルを訓練することにより、テキストデータを分類し、例えば肯定的または否定的な感情、カテゴリ、トピックなどに分類するタスクを実行できます。カスタマーサポートのチャットボットなどのビジネスアプリケーションで役立つ技術です。

誤差逆転伝播法によるニューラルネットワークの学習

誤差逆転伝播法は、ニューラルネットワークの訓練アルゴリズムの一部で、以下の主要なステップから成り立ちます。

1. 順伝播（Forward Propagation）: 訓練データをネットワークに入力し、各層の出力と最終的な予測値を計算します。このとき、各層の重みとバイアスが適用され、モデルの予測が生成されます。
2. 誤差の計算: 予測結果と実際の目標値との誤差を計算します。一般的な誤差関数（例: 平均二乗誤差、交差エントロピー誤差）を使用して誤差を定量化します。
3. 逆伝播（Backward Propagation）: 誤差を出力層から逆向きに伝播させ、各層の重みを更新するための誤差勾配を計算します。誤差勾配は、誤差関数の各パラメータに関しての偏微分です。
4. 重みの更新: 計算された誤差勾配を使用して、各層の重みを微小なステップで更新します。この更新は、最適化アルゴリズム（例: 勾配降下法、Adam）によって行われます。更新された重みにより、次の訓練サンプルに対する予測が改善されます。
5. 繰り返し: 上記のステップを複数の訓練データに対して繰り返し実行し、ネットワークの重みを調整して訓練を続けます。これにより、モデルはデータに適応し、学習します。

ビジネスの応用例

誤差逆転伝播法は、多くのビジネス応用に使用されます。以下はその一例です。

• 手書き数字の認識システム: 銀行のチェック処理やフォーム認識など、手書き数字を自動的に読み取るシステムがあります。誤差逆転伝播法を使用したニューラルネットワークは、これらのシステムで数字認識の精度を向上させるのに役立ちます。ネットワークは大量の手書き数字データセットで訓練され、数字の認識を高精度で実現します。

Pythonコード

# 誤差逆転伝播法は、TensorFlowやKerasのようなフレームワーク内部で自動的に行われます。
# 上記のディープラーニングモデルの訓練時に、このアルゴリズムが適用される。
model.fit(padded, labels, epochs=10)

上記のPythonコードは、ディープラーニングモデルの訓練プロセスを示しています。model.fit()メソッドは、誤差逆転伝播法に基づいて、ニューラルネットワークの重みを訓練データに適応させるために使用されます。このメソッドは、指定されたエポック数（訓練データを何回繰り返して学習するか）に従って重みを更新します。

このような訓練プロセス

により、ネットワークは訓練データに合わせて最適な重みを学習し、新しいデータに対して正確な予測を行うようになります。

ニューラルネットワークの最適化

ニューラルネットワークの最適化は、ネットワークの学習プロセスを改善し、性能を向上させるための手法です。ニューラルネットワークは、数多くの重みとバイアスを持つため、パラメータの調整が必要です。最適化アルゴリズムは、訓練データに基づいて重みを調整する方法を提供します。

• 最適化アルゴリズム: 最適化アルゴリズムは、損失関数を最小化するためのパラメータの更新方法を決定します。一般的な最適化アルゴリズムには、確率的勾配降下法（SGD）、Adam、RMSpropなどがあります。これらのアルゴリズムは、勾配情報を使用して重みを微調整し、損失を最小化しようとします。
• 学習率（Learning Rate）: 学習率は、各更新ステップで重みを調整するステップの大きさを制御します。大きすぎる学習率は収束の問題を引き起こし、小さすぎる学習率は収束が遅い場合があります。適切な学習率を選択することが重要です。
• 損失関数（Loss Function）: 損失関数は、ネットワークの出力と実際の目標値との誤差を評価する方法です。最適化アルゴリズムはこの誤差を最小化しようとします。分類タスクでは交差エントロピー誤差、回帰タスクでは平均二乗誤差などが一般的に使用されます。

ビジネスの応用例

ニューラルネットワークの最適化は、多くのビジネス応用に影響を与えます。以下はその一例です。

• 音声認識システム: 音声認識システムは、音声からテキストに変換するための技術です。高速で正確な音声認識を実現するために、ニューラルネットワークの最適化が必要です。最適なネットワークアーキテクチャと最適化アルゴリズムを選択することで、リアルタイムの音声変換の精度と速度を向上させることができます。

Pythonコード

from tensorflow.keras.optimizers import Adam
optimizer = Adam(learning_rate=0.001)
model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=['accuracy'])

上記のPythonコードでは、Adam最適化アルゴリズムを使用してニューラルネットワークモデルをコンパイルしています。Adam(learning_rate=0.001)で学習率を設定し、model.compile()で最適化アルゴリズム、損失関数、および評価メトリクスを指定しています。この設定により、ニューラルネットワークが訓練中に最適化アルゴリズムを使用してモデルのパラメータを調整します。

勾配消失問題

勾配消失問題は、ディープラーニングモデルが深くなるにつれて、勾配が急速に小さくなり、モデルの重みがほとんど更新されなくなる現象です。この問題は、特に多層のニューラルネットワークで発生しやすく、訓練プロセスが収束しづらくなります。通常、活性化関数や初期化戦略の選択、勾配クリッピングなどの手法が使用されて、この問題を軽減または解決しようとします。

ビジネスの応用例

勾配消失問題の解決は、ディープラーニングモデルをビジネス応用に適用する際に重要です。以下はその一例です。

• 映画レビューの感情分析: 映画のレビューを分析し、感情（肯定的または否定的）を判断するためにディープラーニングを使用する場合、深いニューラルネットワークを構築します。このような場合、勾配消失問題を回避する手法を採用することで、モデルの学習が効率的に進行し、高い性能を実現できます。

Pythonコード

# ReLU活性化関数やその変種（Leaky ReLU, Parametric ReLU）は、勾配消失問題を緩和するのに役立ちます。
from tensorflow.keras.layers import LeakyReLU
model.add(Dense(64))
model.add(LeakyReLU(alpha=0.05))

上記のPythonコードでは、Leaky ReLU活性化関数を使用して勾配消失問題を軽減する方法が示されています。通常のReLU活性化関数は、負の入力に対して勾配が0になり、勾配消失問題が発生しやすいです。しかし、Leaky ReLUは、負の入力に対して小さな勾配を持ち、勾配の消失を軽減します。 LeakyReLU(alpha=0.05)のように設定されたLeaky ReLU関数は、モデルの中間層に適用され、勾配消失問題を緩和するのに役立ちます。

転移学習

転移学習は、あるタスクで訓練されたモデルの一部（または全体）を、新しいタスクのモデルの学習に再利用する機械学習の手法です。通常、既存のモデルは大規模なデータセットで訓練されており、特定の特徴を抽出する能力が高いです。転移学習では、この学習済みモデルをベースにして、新しいタスクに適応できます。これにより、少ないデータや計算リソースで高性能なモデルを構築できます。

ビジネスの応用例

転移学習は、多くのビジネスアプリケーションで利用されます。以下はその一例です。

• 商品認識システム: 既存の画像認識モデル（例：VGG16、ResNet）を使用して、新しい商品を自動的に識別し、在庫管理や顧客サービス向上に役立つシステムを開発します。転移学習により、画像認識の専門知識を持つモデルを効率的に活用できます。

Pythonコード

from tensorflow.keras.applications import VGG16
base_model =
 VGG16(weights='imagenet', include_top=False, input_shape=(150, 150, 3))
for layer in base_model.layers:
    layer.trainable = False
model = Sequential([
    base_model,
    Flatten(),
    Dense(512, activation='relu'),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

上記のPythonコードでは、VGG16という学習済みの画像認識モデルを使用して転移学習を実現しています。以下はコードの主要なポイントです。

1. VGG16モデルは、大規模な画像データセット（ImageNetなど）で訓練されたモデルです。このモデルの一部を再利用します。
2. include_top=Falseは、VGG16モデルの全結合層を含まないことを指定します。これにより、新しいタスクに合わせてカスタム全結合層を追加できます。
3. for layer in base_model.layers: layer.trainable = Falseは、VGG16モデルの層の重みを凍結（更新しない）することを意味します。このようにすることで、転移学習の際に既存の特徴抽出部分を保持し、新しいタスクに適応できます。
4. Sequentialモデルには、VGG16モデルを含むカスタムの層が追加されます。新しいタスクに適した出力層が含まれています。
5. モデルのコンパイルとトレーニングは、通常の方法で行われます。新しいタスクに合わせて適切な損失関数と最適化アルゴリズムを指定します。

畳み込みニューラルネットワーク（CNN）

畳み込みニューラルネットワーク（Convolutional Neural Network、CNN）は、主に画像処理に使用されるディープラーニングモデルです。CNNは、画像などのグリッド状のデータを効果的に処理するために設計され、特に画像認識タスクに適しています。

CNNの主要な特徴は、以下の要素から成り立っています。

1. 畳み込み層 (Convolutional Layer): 画像内の特徴を抽出するための層です。カーネル（フィルタ）を画像上でスライドさせながら、畳み込み演算を行います。これにより、エッジ、テクスチャ、パターンなどの特徴が検出されます。
2. プーリング層 (Pooling Layer): 畳み込み層の出力を縮小し、計算量を削減します。MaxPoolingが一般的で、各領域から最大値を選んでサブサンプリングします。
3. 全結合層 (Fully Connected Layer): 抽出された特徴を使用して、最終的な分類を行うための層です。通常、1つまたは複数の全結合層が含まれます。

ビジネスの応用例

CNNは、さまざまなビジネスアプリケーションで使用されます。以下はその一例です。

• 医療画像解析: 医療画像（X線、MRI、CTスキャンなど）を解析し、疾患の早期検出や病変の識別を支援するためのシステムを開発します。例えば、がんの診断や骨折の検出に利用されます。

Pythonコード

from tensorflow.keras.layers import Conv2D, MaxPooling2D
model = Sequential([
    Conv2D(32, (3, 3), activation='relu', input_shape=(150, 150, 3)),
    MaxPooling2D(2, 2),
    Conv2D(64, (3, 3), activation='relu'),
    MaxPooling2D(2, 2),
    Flatten(),
    Dense(512, activation='relu'),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

上記のPythonコードは、CNNモデルの基本的な構築方法を示しています。以下はコードの主要なポイントです。

1. Conv2D層は、畳み込み層を定義します。この層では、32個の畳み込みフィルタを使用し、ReLU活性化関数を適用します。
2. MaxPooling2D層は、プーリング層を定義します。2×2の領域から最大値を選んでダウンサンプリングします。
3. Flatten層は、畳み込みとプーリングの結果を1次元のベクトルに変換します。
4. Dense層は、全結合層を定義します。最初の層は512ユニットを持ち、ReLU活性化関数が適用され、2番目の層は1ユニットでシグモイド活性化関数が適用されています。
5. モデルのコンパイルは、最適化アルゴリズム（ここでは’adam’）と損失関数（ここでは’binary_crossentropy’）を指定して行われます。また、精度（’accuracy’）も計算されます。

このCNNモデルは、画像認識タスクに適した基本的な構造を持っており、適切にトレーニングされることで、異なるクラスの画像を分類できるようになります。

再帰型ニューラルネットワーク（RNN）

再帰型ニューラルネットワーク（Recurrent Neural Network、RNN）は、順序情報を持つデータに対する処理に適したニューラルネットワークの一種です。通常、時系列データ、テキスト、音声など、データの要素間に順序や依存関係がある場合に使用されます。

RNNの主要な特徴は、以下の要素から成り立っています。

1. 再帰的な結合 (Recurrent Connections): RNNは、前のステップの出力を次のステップの入力として使用する再帰的な結合を持っています。これにより、過去の情報を考慮しながら新しい情報を処理できます。
2. 状態（隠れ状態）: RNN内に状態（hidden state）があり、この状態が情報を保持し、次のステップに伝達されます。これにより、過去のステップでの情報が次のステップに影響を与えます。
3. シーケンスデータの処理: RNNはシーケンスデータに適しており、テキストデータの単語や時系列データの時間ステップごとの処理に使用されます。

ビジネスの応用例

RNNは、ビジネスのさまざまな領域で使用されます。以下はその一例です。

• 株価予測: 過去の株価データを入力として、将来の株価動向を予測するためのモデルを構築します。RNNは時系列データのモデリングに適しており、株価の予測に利用されます。

Pythonコード

from tensorflow.keras.layers import LSTM
model = Sequential([
    Embedding(10000, 64, input_length=100),
    LSTM(64),
    Dense(24, activation='relu'),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

上記のPythonコードは、RNNモデルの基本的な構築方法を示しています。以下はコードの主要なポイントです。

1. Embedding層は、テキストデータの単語埋め込みを行います。これは単語を数値ベクトルに変換するためのもので、単語の意味を捉えるのに役立ちます。
2. LSTM層は、再帰的な処理を行います。LSTM（Long Short-Term Memory）は、RNNの一種で、長期的な依存関係をキャプチャするのに適しています。
3. Dense層は、全結合層を定義します。最初の層は24ユニットを持ち、ReLU活性化関数が適用され、2番目の層は1ユニットでシグモイド活性化関数が適用されています。
4. モデルのコンパイルは、最適化アルゴリズム（ここでは’adam’）と損失関数（ここでは’binary_crossentropy’）を指定して行われます。また、精度（’accuracy’）も計算されます。

このRNNモデルは、シーケンスデータを受け取り、そのシーケンスに関連するタスクを実行するために使用できます。例えば、テキスト分類タスクや時系列予測タスクに適しています。

強化学習とディープラーニング

強化学習:
強化学習は、エージェント（学習するエンティティ）がある環境内で行動し、その行動に対して報酬を受け取りながら、最適な行動戦略を学習する機械学習のアプローチです。エージェントは、環境の状態を観察し、その状態に応じて行動を選択します。行動によって得られる報酬は、エージェントがどれだけ良い行動を選択したかを示し、エージェントは報酬を最大化する行動戦略を学習します。強化学習は、状態、行動、報酬、方策（行動戦略）などの要素から成り立っています。

ディープラーニングと強化学習:
ディープラーニングは、強化学習の一部として使用されることがあります。ディープラーニングは、大規模なニューラルネットワークを使用して高度なパターン認識や制御問題を解決するのに適しています。強化学習にディープラーニングを組み合わせることで、エージェントは複雑な状況においても最適な行動戦略を学習できます。

ビジネスの応用例

強化学習とディープラーニングの組み合わせは、多くのビジネスアプリケーションで使用されています。以下はその一例です。

• 工場の自動化: 工場内でのロボットの制御において、ロボットは異なるタスクを遂行するために強化学習とディープラーニングを使用します。例えば、製品のアセンブリラインでのロボットの動きを最適化し、製品の組み立て速度や品質を向上させます。エージェント（ロボット）は環境（工場）内で動き、報酬（生産効率や品質）を最大化するためにディープラーニングを通じて最適な行動戦略を学習します。

このように、強化学習とディープラーニングの組み合わせは、複雑なタスクの自動化や最適化に役立ちます。ロボット、自動運転車、ゲームAI、金融取引戦略の最適化など、多くの分野で応用されています。

Pythonコード

# 強化学習とディープラーニングの統合は複雑であるため、具体的なコードは省略します。

オートエンコーダ

オートエンコーダ:
オートエンコーダは、入力データを符号化（エンコード）し、それを再構築（デコード）するためのニューラルネットワークです。エンコードとデコードのプロセスで、入力データが圧縮され、その後元のデータに戻されます。オートエンコーダは、次元削減やノイズ除去などのさまざまなタスクに使用されます。

ここで、オートエンコーダの主要な部分を説明します。

1. エンコーダ（Encoder）: 入力データを低次元の表現に変換します。エンコーダは通常、入力データをより小さい次元のベクトルに変換する隠れ層として構成されます。この隠れ層には、データの重要な特徴が抽出されます。
2. デコーダ（Decoder）: エンコードされたデータを元の次元に戻します。デコーダはエンコードされた表現をもとに、元のデータを再構築するためのネットワークです。デコーダの出力は、元の入力データとできるだけ一致するように設計されます。
3. 損失関数（Loss Function）: オートエンコーダのトレーニング時に、再構築誤差を最小化するように損失関数が設定されます。一般的に、二乗誤差や交差エントロピーなどが使用されます。モデルは、エンコードおよびデコードプロセスを最適化し、元のデータとできるだけ似たデータを生成できるように学習します。

ビジネスの応用例

オートエンコーダのビジネスへの応用は多岐にわたります。以下はその一例です。

• ノイズ除去: 製品の画像や音声データからノイズを除去するためにオートエンコーダが使用されます。入力データにノイズが含まれている場合、オートエンコーダはノイズを取り除いたクリアなデータを生成します。
• 次元削減: 高次元のデータを低次元に削減するために使用され、データの可視化や特徴選択に役立ちます。たとえば、顧客の行動データを低次元の特徴ベクトルに変換して、類似性のある顧客セグメントを特定できます。
• 異常検出: 正常なデータの特徴を学習し、異常なデータを検出するために使用されます。異常な振る舞いを持つデータポイントは、通常、高い再構築誤差を持つことが示唆されます。

オートエンコーダは、データの特徴抽出や前処理に幅広く活用され、機械学習とディープラーニングのさまざまなアプリケーションで重要な役割を果たしています。

Pythonコード

from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model
input_img = Input(shape=(784,))
encoded = Dense(128, activation='relu')(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

このコードは、オートエンコーダ（Autoencoder）を定義し、トレーニングのために設定を行うためのTensorFlow/Kerasのコードです。オートエンコーダは、データを圧縮して再構築するためのニューラルネットワークモデルで、通常、データの次元削減やノイズ除去などのタスクに使用されます。

オートエンコーダは入力データをエンコードし、それをデコードして再構築します。このプロセスで、データの次元削減やノイズ除去などのタスクが実行されます。そして、訓練中にモデルはエンコードとデコードのプロセスを最適化し、元のデータに近い表現を生成するように学習します。

GAN（敵対的生成ネットワーク）

GAN（Generative Adversarial Network）は、生成モデルとして知られるモデルの一種で、生成器（Generator）と判別器（Discriminator）と呼ばれる2つのニューラルネットワークが相互に競合して学習するアーキテクチャです。

GANは、生成器と判別器の2つの主要なコンポーネントで構成されています。

1. 生成器（Generator）: 生成器は、ランダムノイズまたは他のデータを受け取り、それを元に新しいデータを生成しようとするネットワークです。例えば、ランダムなノイズからリアルな画像を生成しようとする場合、生成器はその役割を果たします。生成器の目標は、できるだけリアルなデータを生成することです。
2. 判別器（Discriminator）: 判別器は、生成器が生成したデータと実際のデータを区別する役割を果たします。つまり、判別器は与えられたデータが本物のデータであるか、それとも生成器によって作成された偽のデータであるかを識別します。判別器はバイナリ分類器として機能し、1つのクラスが「本物」で、もう1つのクラスが「偽物」です。

GANの学習プロセスは、次のステップで進行します。

1. 生成器の学習: 生成器はランダムノイズまたは他のデータを入力として受け取り、それを使ってデータを生成します。生成器は生成したデータを判別器に提供し、判別器がそれを「本物」と誤認識するように努力します。生成器の目標は、判別器を欺くように高品質なデータを生成することです。
2. 判別器の学習: 判別器は、本物のデータと生成されたデータを受け取り、それらを区別する方法を学習します。判別器は本物のデータを「本物」と正確に認識し、生成されたデータを「偽物」と識別しようと努力します。
3. 競争と調整: 生成器と判別器は相互に競争し合い、学習が進むにつれて改善します。生成器は判別器を欺くように生成を洗練させ、判別器は生成器が生成したデータをより正確に識別しようと努力します。この競争的なプロセスにより、生成器は本物に近いデータを生成できるようになります。

ビジネスの応用例

GANは多くのビジネス応用に役立ちます。例えば：

1. 新しいデータの生成: GANは、既存のデータから新しいデータを生成するために使用できます。これは、新製品のデザイン、建物や都市のシミュレーション、アート生成などに適用できます。
2. 画像の超解像度化: GANは、低解像度の画像を高解像度に変換するタスクに使用できます。これは、メディア制作や映像編集の分野で有用です。
3. データ拡張: GANは、データセットを拡張し、モデルの性能を向上させるために使用できます。特に、少ないデータで深層学習モデルをトレーニングする場合に役立ちます。

GANはとてもパワフルで創造的なモデルであり、多くのアプリケーションで革新的なソリューションを提供しています。

Pythonコード

# GANの実装は複雑であるため、具体的なコードは省略します。

物体検出

物体検出は、ディープラーニングの応用分野の1つで、画像内の複数の物体を同時に識別し、その位置を特定する技術です。

物体検出は、コンピュータビジョンのタスクで、画像内の物体を特定し、その位置を矩形領域（バウンディングボックス）で囲み、物体のクラス（カテゴリ）を識別することを目的とします。ディープラーニングを用いた物体検出では、主に以下の2つのアプローチが一般的です。

1. 領域提案ベースの方法（R-CNN、Fast R-CNN、Faster R-CNNなど）: このアプローチでは、まず画像内から物体の存在が疑われる領域を提案（検出）します。提案された領域を切り取り、各領域を個別にクラス分類します。この方法は、領域提案に対して個別の畳み込みネットワーク（CNN）を使用します。
2. 単一のエンドツーエンドネットワーク（YOLO、SSDなど）: このアプローチでは、画像全体に対して一度の推論を行い、各物体の位置とクラスを同時に予測します。この方法は高速でリアルタイムのアプリケーションに適しています。

ビジネスの応用例

物体検出のディープラーニング技術は、さまざまなビジネス応用に使用されます。例えば：

1. セキュリティと監視: 監視カメラの映像から不審者や異常な行動を検出し、セキュリティ対策に役立ちます。また、防犯カメラを用いて監視エリア内の物体を自動的に追跡するためにも使用されます。
2. 自動運転: 自動運転車載カメラは、道路上の他の車両や歩行者を検出し、運転支援システムを制御するために物体検出技術を使用します。
3. 小売業: 商品の棚から品切れ品を検出し、在庫管理や補充のための情報を提供します。
4. 製造業: 製造プロセス中の不良品を自動的に検出し、品質管理を向上させます。

物体検出は、ディープラーニングの応用の中でもとても重要で、多くの産業分野で効果的に利用されています。

Pythonコード

# 物体検出の実装は多岐にわたるため、具体的なコードは省略します。

機械学習用ライブラリとフレームワーク

機械学習用ライブラリとフレームワークは、機械学習のモデルを構築し、訓練するためのツールやリソースの集まりです。これらは、機械学習プロジェクトを効率的に実施するために使用されます。

1. 機械学習ライブラリ: 機械学習ライブラリは、基本的な機械学習アルゴリズムやツールを提供するソフトウェアパッケージです。これらのライブラリには、データの前処理、モデルのトレーニング、評価、モデルの保存と読み込みなど、機械学習タスクをサポートする多くの便利な機能が含まれています。例として、scikit-learn（Pythonのライブラリ）があります。
2. 機械学習フレームワーク: 機械学習フレームワークは、より高度なモデルやニューラルネットワークを構築し、訓練するためのより高度なツールを提供します。これらのフレームワークは、ニューラルネットワークの構築、自動微分、GPUサポート、分散トレーニングなど、高度な機能を提供します。例として、TensorFlowやPyTorchがあります。

ビジネスの応用例

機械学習用ライブラリとフレームワークは、ビジネスにおいてさまざまな用途で活用されます。

1. カスタマーアナリティクス: 顧客の購買履歴と行動データを解析し、次の購買を予測するモデルを構築します。これにより、ターゲットマーケティング戦略を最適化できます。
2. 製品品質管理: 製造プロセスから得られるセンサーデータを使用して、不良品の早期検出モデルを開発し、生産プロセスを改善します。
3. 金融予測: 株式市場や財務データを分析し、将来のトレンドやリスクを評価するための予測モデルを構築します。これにより、投資ポートフォリオの最適化が可能です。
4. 自然言語処理: テキストデータから情報抽出、感情分析、テキスト生成などのタスクに対するモデルを構築し、カスタマーサポートやコンテンツ生成を向上させます。
5. 画像処理: 画像データから物体検出、顔認識、画像分類などのタスクに対するモデルを構築し、セキュリティ監視や医療診断などの応用に使用します。

Pythonコード

# scikit-learnやTensorFlow、PyTorchなどのライブラリやフレームワークがあります。
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()
clf.fit(X_train, y_train
)

上記のPythonコードでは、scikit-learnライブラリを使用したランダムフォレスト分類器の訓練が示されており、ライブラリを使った簡単な機械学習モデルの構築と訓練方法を示しています。

ディープラーニングのフレームワーク

ディープラーニングのフレームワークは、ディープニューラルネットワークのモデルの構築、訓練、評価に役立つツール群です。これらのフレームワークは、ディープラーニングのプロジェクトを効率的に実施するための基盤を提供します。

1. モデルの構築: ディープラーニングフレームワークは、ニューラルネットワークモデルのアーキテクチャを定義するためのツールを提供します。これには畳み込み層、全結合層、リカレント層などの異なる種類のレイヤーを組み合わせてモデルを設計できます。
2. 訓練: フレームワークは、モデルを訓練するための機能を提供します。訓練には、データの読み込み、モデルの重みの更新、損失関数の最小化などが含まれます。さらに、GPUや分散トレーニングをサポートすることで、大規模なデータセットでの高速な訓練が可能です。
3. 評価: モデルの性能を評価するためのメトリクスや評価関数を提供します。これにより、モデルの性能を定量的に評価できます。

ビジネスの応用例

ディープラーニングのフレームワークは、ビジネスにおいてさまざまな用途で活用されます。

1. 感情分析: ソーシャルメディア上の顧客の感情を分析し、製品やサービスへの感想を理解します。これにより、製品改善やマーケティング戦略の最適化が可能です。
2. 顔認識: カメラ映像からの顔認識により、セキュリティアクセスの制御や顧客の年齢や性別の推定など、さまざまな用途に利用できます。
3. 自動運転: 自動車産業では、センサーデータを解析し、自動運転車の制御に使用される高度なニューラルネットワークを構築します。
4. 自然言語処理: テキストデータの解析により、カスタマーサポートの自動化、文書の要約、言語翻訳などが可能です。
5. 医療診断: 医療画像の解析により、病気の早期発見や診断の支援を行います。

Pythonコード

# TensorFlowやPyTorch、Kerasなどのフレームワークがあります。
import tensorflow as tf
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(512, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

上記のPythonコードでは、TensorFlowを使用してニューラルネットワークモデルを構築し、訓練および評価する方法が示されています。このコードは、手書き数字の認識などのタスクに使用できます。

IT起業家

▼AIを使った副業・起業アイデアを紹介♪