2024年版【GCP資格の勉強 PDE編】機械学習のモデルの検証 – 交差検証 / 予測誤差 / 分類 / 回帰とは？

2024年版【GCP資格の勉強 PDE編】

2024年版【GCP資格の勉強 PDE編】機械学習のモデルの検証 – 交差検証 / 予測誤差 / 分類 / 回帰とは？について解説します。
（★注意：GCP資格 Professional Data Engineer(PDE)試験の公式テキスト・問題集などを元に独自にまとめたものです）

Google Cloud Platform（GCP）のProfessional Data Engineer（PDE）試験において、機械学習モデルの検証は重要なトピックの一つです。モデルの検証には、交差検証、予測誤差の評価、分類モデルおよび回帰モデルの評価方法が含まれます。機械学習モデルの検証について詳しく見ていきましょう。

交差検証（Cross-Validation）

交差検証（Cross-Validation）は、機械学習でモデルの性能を評価するための一般的な手法です。機械学習のモデルの検証を理解するために、まず基本的な概念を説明します。

機械学習では、モデル（アルゴリズム）を使ってデータから学習し、新しいデータに対する予測を行います。しかし、モデルがどれだけうまく機能するかを知るためには、まだ見ぬデータに対するモデルの予測能力を評価する必要があります。これを行う方法はいくつかあり、交差検証はそのひとつです。

交差検証の目的と特徴

交差検証の主な目的は、モデルの性能をより正確に評価することです。交差検証は、以下のようなステップで行われます。

  1. データセットの分割: まず、利用可能なデータセットを小さなグループまたは「サブセット」に分割します。
  2. テストとトレーニング: 次に、サブセットのうちの一つを選び、モデルのテストに使用します。残りのサブセットはモデルのトレーニング（学習）に使われます。
  3. 繰り返しプロセス: このプロセスを繰り返し、それぞれのサブセットが一度はテストセットとして使われるようにします。

k分割交差検証（k-fold cross-validation）

k分割交差検証は、交差検証の一種で、以下のように進められます。

  1. データセットの分割: データセットをk個のサブセットに均等に分割します。
  2. 繰り返しプロセス: それぞれのサブセットを一度はテストセットとして使用し、残りのk-1個のサブセットでモデルをトレーニングします。
  3. 結果の集計: 各サブセットでのテスト結果を集計し、モデルの平均的な性能を評価します。

k分割交差検証は、モデルが特定のデータセットに過度に適合してしまうこと（過学習）を防ぐのに役立ち、より一般化されたモデルの評価を可能にします。また、データセットのサイズが小さい場合に特に有用です。

目的と特徴：: モデルの性能をより正確に評価するために、データセットを複数のサブセットに分割し、それぞれのサブセットでモデルをテストします。
最も一般的な方法はk分割交差検証（k-fold cross-validation）で、データセットをk個のサブセットに分割し、そのうちの一つをテストセットとして使用し、残りをトレーニングセットとして使用します。このプロセスをk回繰り返します。

Pythonコードの概要

from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt

# Sample data creation
# Creating a simple dataset with a linear relationship
np.random.seed(0)
X = np.random.rand(100, 1) * 10  # Independent variable
y = 2 * X + np.random.randn(100, 1) * 2  # Dependent variable with some noise

# k-fold cross-validation (k=5)
kf = KFold(n_splits=5)
model = LinearRegression()
mse_list = []

# Iterate over each split
for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    # Train the model
    model.fit(X_train, y_train)

    # Predict and calculate MSE
    y_pred = model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    mse_list.append(mse)

# Calculate average MSE
average_mse = np.mean(mse_list)

# Plotting
plt.scatter(X, y, color='blue', label='Data Points')
plt.plot(X, model.predict(X), color='red', label='Linear Fit')
plt.xlabel('Independent Variable')
plt.ylabel('Dependent Variable')
plt.title('Linear Regression with k-fold Cross-Validation')
plt.legend()
plt.show()

average_mse, mse_list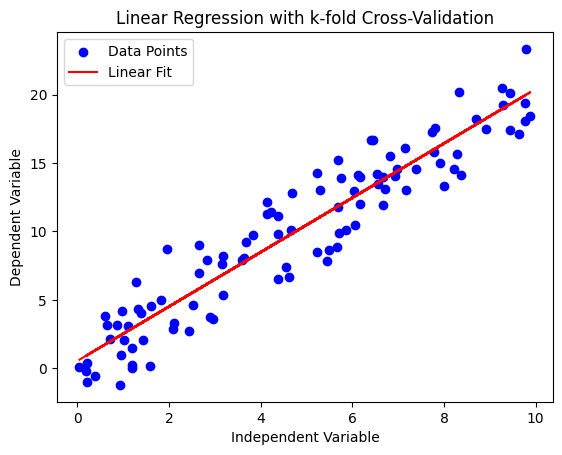
2024年版【GCP資格の勉強 PDE編】機械学習のモデルの検証 - 交差検証 / 予測誤差 / 分類 / 回帰とは？ | 単純な線形回帰モデルを用いたk分割交差検証の実演
単純な線形回帰モデルを用いたk分割交差検証の実演
(4.178864564374733,
 [3.8094525062943996,
  6.239669381246973,
  2.482103365888045,
  4.762769319402642,
  3.6003282490416018])

上記のPythonコードは、単純な線形回帰モデルを用いたk分割交差検証の実演を示しています。以下はコードとその出力の概要です。

  1. データ生成: 線形関係を持つサンプルデータセットを生成します。独立変数 X はランダムな配列で、従属変数 y は X に線形に関連しており、いくつかのノイズが加えられています。
  2. k分割交差検証の設定: 5分割の交差検証（k=5）を使用します。データセットが5つのサブセットに分割されることを意味します。
  3. モデルのトレーニングと評価:
    各イテレーションで、LinearRegression モデルは4つのサブセットでトレーニングされ、5番目のサブセットでテストされます。
    モデルの性能を評価するために、各テストサブセットの平均二乗誤差（MSE）が計算されます。
  4. 結果の計算:
    すべての分割にわたる平均MSEが計算され、モデルの全体的な性能指標を提供します。
  5. プロット:
    散布図は元のデータポイントを示しています。
    線形フィットラインは、データセット全体に対するモデルの予測を表しています。

出力

平均MSE: すべての分割にわたる平均二乗誤差は約4.18です。平均二乗誤差の値は、モデルの予測の平均誤差を示しています。
MSEリスト: リストには5つの分割のそれぞれのMSEが含まれており、モデルの性能がデータの異なるサブセットにどのように変化したかを示しています。

プロットは、線形関係と線形回帰モデルのフィットを視覚的に示しています。交差検証アプローチにより、モデルの性能がより堅牢に評価され、特定のサブセットのデータに過学習するリスクが減少します。

【練習問題】交差検証（Cross-Validation）

  • 問題1:
    あなたは5分割交差検証を使用して機械学習モデルを評価しています。この場合、データセットはどのように使用されますか？
  • A. データセット全体が5回、テストセットとして使用されます。
    B. データセットの5分の1がテストセットとして、残りの4分の1がトレーニングセットとして5回使用されます。
    C. データセット全体が一度だけテストセットとして使用されます。
    D. データセット全体が一度だけトレーニングセットとして使用されます。
  • 解答: B. データセットの5分の1がテストセットとして、残りの4分の1がトレーニングセットとして5回使用されます。
  • 解説:
    5分割交差検証では、データセットは5つの等しい部分に分割されます。各イテレーションで、異なるサブセットがテストデータとして使用され、残りの部分がトレーニングデータとして使用されます。これにより、データセットの各部分が正確に一度、テストセットとして使われます。
  • 問題2:
    交差検証において、各イテレーションで異なるサブセットがテストデータとして使用される目的は何ですか？
  • A. データの多様性を確保するため
    B. モデルの過学習を防ぐため
    C. 計算時間を短縮するため
    D. すべてのデータを使用するため
  • 解答: B. モデルの過学習を防ぐため
  • 解説:
    異なるサブセットをテストデータとして使用することで、モデルが特定のデータセットに過度に適合してしまうこと（過学習）を防ぐことができます。モデルの汎用性が向上し、未知のデータに対する予測能力が正確に評価されます。
  • 問題3:
    k分割交差検証において、kの値が大きすぎるとどのような問題が生じる可能性がありますか？
  • A. モデルの訓練時間が長くなる
    B. モデルがデータを過学習する
    C. モデルの精度が低下する
    D. モデルの予測能力が向上する
  • 解答: A. モデルの訓練時間が長くなる
  • 解説:
    kの値が大きいと、モデルはより多くのイテレーションで訓練される必要があります。モデルの訓練にかかる時間が長くなり、計算リソースの使用が増加します。また、小さなトレーニングセットでモデルを訓練することになるため、過学習のリスクも若干増加する可能性があります。

予測誤差（Prediction Error）

予測誤差（Prediction Error）は、機械学習モデルの予測がどれだけ正確かを測定するための指標です。モデルがどのようなタイプかによって、予測誤差を評価する方法が異なります。

分類モデルの誤差

分類モデルは、データを異なるカテゴリ（例：「スパム」または「非スパム」）に分類します。分類モデルの性能は、以下のように評価されます。

  • 混同行列（Confusion Matrix）: 混同行列は、モデルがどのように分類を行ったかを示す表です。混同行列の表には、以下の4つの要素が含まれます。
    • 真陽性（TP: True Positive）: モデルが正しく肯定的な予測をしたケース。
    • 偽陽性（FP: False Positive）: モデルが誤って肯定的と予測したケース。
    • 真陰性（TN: True Negative）: モデルが正しく否定的な予測をしたケース。
    • 偽陰性（FN: False Negative）: モデルが誤って否定的と予測したケース。
  • 精度（Accuracy）: モデルが正しく予測したケースの割合。
  • リコール（Recall）: 正のケースのうち、モデルが正しく検出した割合。
  • 精度（Precision）: モデルが肯定的と予測したケースのうち、正しく肯定的だった割合。
  • F1スコア: 精度とリコールのバランスを取った指標。

回帰モデルの誤差

回帰モデルは、数値を予測します（例：家の価格）。回帰モデルの性能は以下のように評価されます。

  • 平均絶対誤差（MAE: Mean Absolute Error）: 予測と実際の値との差の絶対値の平均。
  • 平均二乗誤差（MSE: Mean Squared Error）: 予測と実際の値との差の二乗の平均。
  • 平均二乗平方根誤差（RMSE: Root Mean Squared Error）: MSEの平方根。
  • R2スコア: モデルの予測が実際のデータにどれだけ適合しているかを示す指標。

これらの指標は、モデルがどれだけ予測において正確であるかを評価するのに役立ちます。分類モデルはカテゴリーを、回帰モデルは連続する数値を予測する点が異なります。

【練習問題】予測誤差（Prediction Error）

  • 問題1:
    ある分類モデルが、100個のサンプルに対して予測を行いました。結果は次の通りです：50個の真陽性（TP）、10個の偽陽性（FP）、30個の真陰性（TN）、10個の偽陰性（FN）。このモデルの精度（Accuracy）は何％ですか？
  • A. 80％
    B. 50％
    C. 70％
    D. 60％
  • 解答: A. 80％
  • 解説:
    精度（Accuracy）は、モデルが正しく予測したケースの割合を示します。計算式は (TP + TN) / 全サンプル数 です。この場合、(50 + 30) / 100 = 80/100 = 0.80 つまり、80％です。
  • 問題2:
    回帰モデルの性能を評価するために、平均絶対誤差（MAE）と平均二乗誤差（MSE）のどちらを使用すると、大きな誤差を持つサンプルの影響がより強く反映されますか？
  • A. 平均絶対誤差（MAE）
    B. 平均二乗誤差（MSE）
    C. 両方同じ
    D. どちらも反映されない
  • 解答: B. 平均二乗誤差（MSE）
  • 解説:
    MSEは誤差を二乗するため、大きな誤差を持つサンプルが全体の誤差に与える影響が強くなります。一方、MAEは誤差の絶対値を平均するため、大きな誤差の影響がMSEほど強くなりません。
  • 問題3:
    ある分類モデルが高い精度（Accuracy）を示していますが、リコール（Recall）が低い場合、どのような問題が考えられますか？
  • A. モデルが多くの偽陽性（FP）を生成している
    B. モデルが多くの真陽性（TP）を見逃している
    C. モデルが多くの真陰性（TN）を生成している
    D. モデルが多くの偽陰性（FN）を生成している
  • 解答: D. モデルが多くの偽陰性（FN）を生成している
  • 解説:
    リコール（Recall）は、正のケースのうちモデルが正しく検出した割合を示します。リコールが低いということは、モデルが正のケースを見逃し（偽陰性を生成）、それらを否定的と誤分類していることを意味します。精度が高くてもリコールが低い場合、モデルは肯定的なケースを効果的に識別できていない可能性があります。

分類モデルの評価

分類モデルの評価は、そのモデルがどれだけ正確にカテゴリ（クラス）を予測できるかに基づいて行われます。特に、「AUC-ROCカーブ」というツールが分類モデルの全体的な性能を評価するのによく使われます。

分類モデルの性能評価

分類モデルは、例えばメールが「スパム」か「非スパム」かのように、データを特定のカテゴリに分類します。モデルの性能は、どれだけ正確にカテゴリを予測できるかで評価されます。

AUC-ROCカーブ

  • ROCカーブ: 「ROCカーブ（Receiver Operating Characteristic curve）」は、モデルがクラスをどれだけうまく識別できるかを示します。具体的には、横軸に「偽陽性率（False Positive Rate）」、縦軸に「真陽性率（True Positive Rate）」をプロットしたグラフです。
    • 真陽性率: 正しいクラスを正しく予測した割合。
    • 偽陽性率: 誤ったクラスを誤って予測した割合。
  • AUC（Area Under Curve）: ROCカーブ下の面積を「AUC」といいます。AUCが大きいほど、モデルの性能が良いと判断されます。AUCは0から1までの値を取り、1に近いほどモデルの識別能力が高いことを意味します。

AUC-ROCカーブは、分類モデルが異なるクラスをどれだけうまく区別できるかを視覚的に理解するのに役立ちます。高いAUCを持つモデルは、正しいクラスを効果的に識別できると考えられます。

【練習問題】分類モデルの評価

  • 問題1:
    ある分類モデルのROCカーブが描かれています。このカーブのAUC（Area Under Curve）の値が0.9である場合、モデルの性能についてどのように評価できますか？
  • A. モデルはあまり効果的ではない。
    B. モデルはかなり良好な性能を持つ。
    C. モデルの性能は平均的である。
    D. モデルの性能について何も言えない。
  • 解答: B. モデルはかなり良好な性能を持つ。
  • 解説:
    AUCの値が0.9ということは、モデルが異なるクラスをとても効果的に区別できることを意味します。AUCが1に近いほど、モデルの識別能力が高いと判断されるため、0.9はかなり良い性能を示しています。
  • 問題2:
    分類モデルが偽陽性率が0で真陽性率が1の点に位置するROCカーブを持つ場合、モデルの性能についてどう評価できますか？
  • A. モデルは完璧な性能を持つ。
    B. モデルは平均的な性能を持つ。
    C. モデルは効果的ではない。
    D. モデルの性能は低い。
  • 解答: A. モデルは完璧な性能を持つ。
  • 解説:
    偽陽性率が0で真陽性率が1ということは、モデルがすべての正のケースを正しく識別し、誤ったクラスを一切予測していないことを意味します。これは、理想的な状況であり、モデルの性能は完璧と評価できます。
  • 問題3:
    ある分類モデルのAUCが0.5である場合、モデルの性能についてどのように評価できますか？
  • A. モデルは効果的ではない。
    B. モデルは平均的な性能を持つ。
    C. モデルはかなり良好な性能を持つ。
    D. モデルの性能はとても低い。
  • 解答: A. モデルは効果的ではない。
  • 解説:
    AUCが0.5ということは、モデルの識別能力がランダムな推測と同じであることを意味します。つまり、モデルは異なるクラスを効果的に区別できていないと評価できます。

回帰モデルの評価

回帰モデルとは

回帰モデルは、数値を予測するためのモデルです。例えば、家の価格や気温などの連続する数値を予測する際に使われます。

回帰モデルの評価の特徴

  • 連続値の予測精度: 回帰モデルの評価は、モデルがどれだけ正確に連続値（数値）を予測できるかに基づいて行われます。つまり、モデルの予測値が実際の値にどれだけ近いかを測定します。
  • 誤差指標の選択: モデルの評価にはさまざまな誤差指標があります。データの性質によって、どの指標を使うかを選ぶ必要があります。主な誤差指標には以下のようなものがあります。
    • 平均絶対誤差（MAE: Mean Absolute Error）: 予測値と実際の値の差の絶対値の平均。
    • 平均二乗誤差（MSE: Mean Squared Error）: 予測値と実際の値の差の二乗の平均。
    • 平均二乗平方根誤差（RMSE: Root Mean Squared Error）: MSEの平方根。
    • R2スコア: モデルがデータにどれだけ適合しているかを示す指標。

回帰モデルの評価は、モデルが実際の数値をどれだけ正確に予測できるかに焦点を当てています。適切な誤差指標を選ぶことで、モデルの性能を適切に評価できます。

【練習問題】回帰モデルの評価

  • 問題1:
    ある回帰モデルが家の価格を予測しました。実際の価格とモデルの予測価格との差が以下のようになっています：[10, -5, 2, -1, 4]（単位：万円）。このモデルの平均絶対誤差（MAE）は何万円ですか？
  • 解答:
    4万円
  • 解説:
    平均絶対誤差（MAE）は予測値と実際の値の差の絶対値の平均です。この場合、差の絶対値は [10, 5, 2, 1, 4] となり、その平均は (10 + 5 + 2 + 1 + 4) / 5 = 22 / 5 = 4.4 となります。したがって、平均絶対誤差は4万円です。
  • 問題2:
    ある回帰モデルの平均二乗誤差（MSE）が25で、平均二乗平方根誤差（RMSE）を求めてください。
  • 解答:
    5
  • 解説:
    平均二乗平方根誤差（RMSE）は、平均二乗誤差（MSE）の平方根です。MSEが25の場合、RMSEは √25 = 5 となります。これは、モデルの予測が実際の値から平均で5単位ずれていることを意味します。
  • 問題3:
    回帰モデルがデータに完全に適合している場合、R2スコアはどのような値になりますか？
  • A. 0
    B. 0.5
    C. 1
    D. -1
  • 解答:
    C. 1
  • 解説:
    R2スコアは、モデルがデータにどれだけ適合しているかを示す指標で、0から1までの値を取ります。モデルがデータに完全に適合している場合、R2スコアは最大値である1になります。これは、モデルが実際のデータを完全に説明していることを意味します。

まとめ

GCPでは、機械学習モデルの検証と評価は、AI Platform、BigQuery ML、TensorFlowなどのツールを使用して行われます。PDE試験では、機械学習モデルの検証方法の理解と、実際のデータセットに適用する能力が試されます。

また、ビジネスや実世界のシナリオにおいて機械学習モデルの評価方法をどのように適用するかについての理解も求められます。

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


前の記事

【Python】都市の人口動態からの交通ニーズを予測
【Python】人工知能(AI)で都市の人口動態から交通ニーズ…

次の記事

2024年版【GCP資格の勉強 PDE編】Data Aggre…
2024年版【GCP資格の勉強 PDE編】